Problem statement














- the orthic triangle is obtuse isosceles
- radius
 is parallel to side
is parallel to side 
- the nine-point center lies on

- the geometric mean theorem holds
- the bisector of
 has length
has length  , where
, where 
- segment
 is tangent to the circumcircle at point
is tangent to the circumcircle at point 
- the orthocenter is a reflection of vertex
 over side
over side  .
.
The connection between the orthic triangle and the geometric mean theorem seems cool. The restriction to non-right triangles is crucal: some of the statements hold in right triangles, but not the entire chain of statements.
Our favorites: ![]() . Notice the last two.
. Notice the last two.
Partial solutions
A complete proof will require about ![]() implications, and we’ve already seen some of these implications in previous iterations of our discussions: May 14, May 28, June 14, and June 28. Below we make some random selections.
implications, and we’ve already seen some of these implications in previous iterations of our discussions: May 14, May 28, June 14, and June 28. Below we make some random selections.
To be specific, let ![]() and set
and set ![]() . Then
. Then ![]() and
and ![]() . Consider the circumcircle shown below:
. Consider the circumcircle shown below:
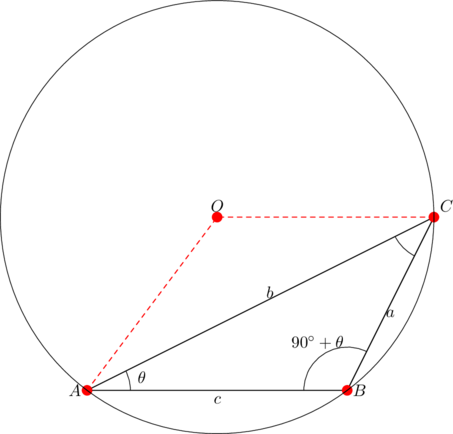
The angle which the major arc ![]() subtends at the center of the circle is twice the angle it subtends at the circumference, and so:
subtends at the center of the circle is twice the angle it subtends at the circumference, and so:
![]()
Since ![]() is isosceles, we have that
is isosceles, we have that
![]()
This shows that ![]() is parallel to
is parallel to ![]() .
.
Begin by drawing the circumcircle:
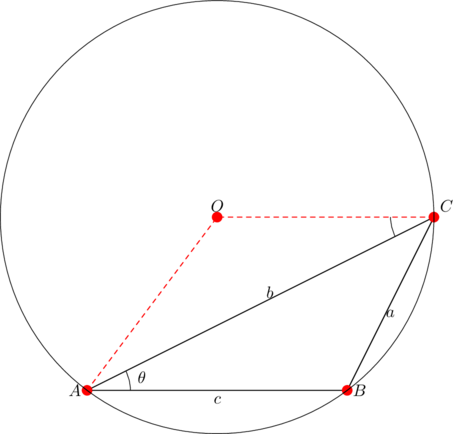
If ![]() , then
, then ![]() , as marked above. Reason: radius
, as marked above. Reason: radius ![]() is parallel to side
is parallel to side ![]() by assumption. Next,
by assumption. Next, ![]() is isosceles, and so
is isosceles, and so ![]() . In turn, this yields
. In turn, this yields ![]() . The major arc
. The major arc ![]() now subtends an angle of
now subtends an angle of ![]() at the center of the circle. This means that it subtends an angle of
at the center of the circle. This means that it subtends an angle of ![]() at the circumference. Thus,
at the circumference. Thus, ![]() . The difference between
. The difference between ![]() and
and ![]() is then
is then ![]() .
.
A different orientation having angle ![]() placed at
placed at ![]() will also yield the same conclusion.
will also yield the same conclusion.
Let ![]() and set
and set ![]() . Then
. Then ![]() and
and ![]() . Draw the circumcircle, like so:
. Draw the circumcircle, like so:
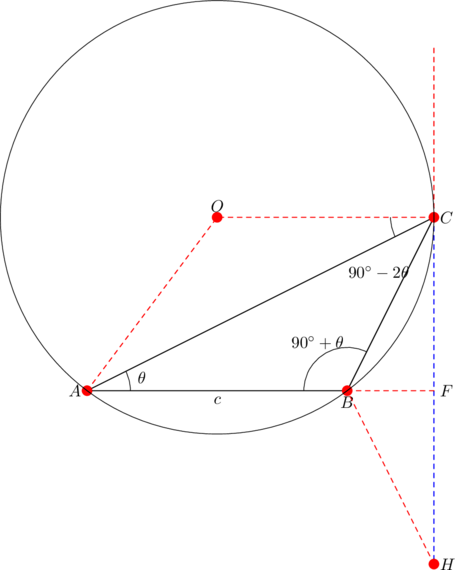
Since ![]() is obtuse, its orthocenter
is obtuse, its orthocenter ![]() is situated outside the triangle as shown above. Join
is situated outside the triangle as shown above. Join ![]() and
and ![]() . Extend side
. Extend side ![]() to meet
to meet ![]() at
at ![]() . Since
. Since ![]() now becomes the foot of the altitude from
now becomes the foot of the altitude from ![]() , we have that
, we have that ![]() . Since
. Since ![]() is parallel to
is parallel to ![]() , it follows that
, it follows that ![]() .
.
Radius is perpendicular to tangent at the point of contact. Implies: ![]() is a tangent to the circumcircle at
is a tangent to the circumcircle at ![]() .
.
Apply the Pythagorean theorem to the right triangle ![]() below:
below:
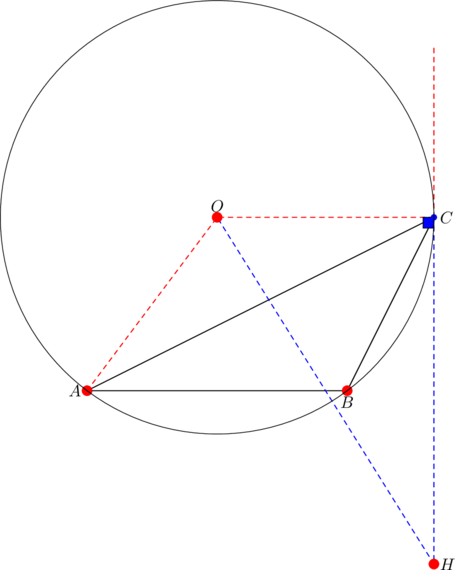
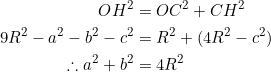
We had ![]() from the preceding example. This in turn implies
from the preceding example. This in turn implies ![]() . So
. So ![]() below is isosceles with
below is isosceles with ![]() :
:

Extend side ![]() to meet
to meet ![]() at
at ![]() . Since
. Since ![]() now becomes the foot of the altitude from
now becomes the foot of the altitude from ![]() , we have that
, we have that ![]() . Altitude
. Altitude ![]() bisects the base, so
bisects the base, so ![]() . This proves that
. This proves that ![]() is a reflection of
is a reflection of ![]() over side
over side ![]() .
.
We focus on the internal case and use the segment addition postulate. Note that in any triangle ![]() with orthocenter
with orthocenter ![]() , circumcenter
, circumcenter ![]() , and nine-point center
, and nine-point center ![]() we have:
we have:
![]()
We proved before that ![]() when
when ![]() . So
. So
![]()
After some simplifications, we obtain
![]()
Similarly:
![]()
Let’s examine the absolute values. There are four cases to consider.
First, we can’t have ![]() and
and ![]() simultaneously. Otherwise, their sum must be greater than zero as well; but their sum is
simultaneously. Otherwise, their sum must be greater than zero as well; but their sum is ![]() .
.
Next, suppose that ![]() and
and ![]() . Then the sum is
. Then the sum is ![]() , and so:
, and so:
![]()
Because ![]() , this leads to
, this leads to ![]() . This is a special case. If the points
. This is a special case. If the points ![]() aren’t co-linear, then in
aren’t co-linear, then in ![]() , the median through
, the median through ![]() passes through the nine-point circle, and so the length of this median is a radius of the nine-point circle, namely
passes through the nine-point circle, and so the length of this median is a radius of the nine-point circle, namely ![]() . We now have a triangle
. We now have a triangle ![]() in which the sum of two sides is
in which the sum of two sides is ![]() and a median has length
and a median has length ![]() . This is impossible (see the exercises at the end). Indeed, the side-lengths of
. This is impossible (see the exercises at the end). Indeed, the side-lengths of ![]() have to be of the form
have to be of the form ![]() for sides
for sides ![]() (or sides
(or sides ![]() ). If we compute the cosine of the angle at
). If we compute the cosine of the angle at ![]() , we obtain
, we obtain
![Rendered by QuickLaTeX.com \[\cos N=\frac{\left(\frac{R-c}{2}\right)^2+\left(\frac{R+c}{2}\right)^2-c^2}{2\times \frac{R-c}{2}\times \frac{R+c}{2}}=1\implies\angle N=0\]](https://blog.fridaymath.com/wp-content/ql-cache/quicklatex.com-98aa0f1576b365c0b50d0a0a2e263d70_l3.png)
The third and fourth cases are the same. For example, ![]() and
and ![]() . Then take
. Then take
![]()
and obtain
![]()
Using the fact that ![]() , we have:
, we have:
![]()
After all the trouble of the previous example, we don’t want to bother you with another seemingly lengthy procedure, but note that ![]() results after simplifications.
results after simplifications.
Normally, ![]() . So
. So
![Rendered by QuickLaTeX.com \[ab\left(1-\left(\frac{c}{a+b}\right)^2\right)= \frac{2a^2b^2}{a^2+b^2}\implies (a^2-b)^2=(ac)^2+(cb)^2\]](https://blog.fridaymath.com/wp-content/ql-cache/quicklatex.com-698acf3ef9bd0d53e3421ddd4fbf8ab8_l3.png)
First isolate ![]() from
from ![]() as
as ![]() and then use in the standard angle bisector formula:
and then use in the standard angle bisector formula:
![Rendered by QuickLaTeX.com \[l^2=ab\left(1-\left(\frac{c}{a+b}\right)^2\right)=\frac{2a^2b^2}{a^2+b^2}.\]](https://blog.fridaymath.com/wp-content/ql-cache/quicklatex.com-84d8f49118edad09420084190c79698e_l3.png)
Peculiar scenario
Below is a reward of the labour in example 6.
Take ![]() with
with ![]() . Then
. Then ![]() . The nine-point center is precisely
. The nine-point center is precisely ![]() , since (according to example 6):
, since (according to example 6):
![]()
Our next post will show that no other triangle has this property.
Takeaway
Let ![]() be a non-right triangle with side-lengths
be a non-right triangle with side-lengths ![]() , altitudes
, altitudes ![]() , circumradius
, circumradius ![]() , circumcenter
, circumcenter ![]() , orthocenter
, orthocenter ![]() , and nine-point center
, and nine-point center ![]() . Then the following statements are equivalent:
. Then the following statements are equivalent:



















- radius
 is parallel to side
is parallel to side 
- segment
 is tangent to the circumcircle at point
is tangent to the circumcircle at point 
- the nine-point center lies on

- the orthic triangle is obtuse isosceles
- the geometric mean theorem holds
- the bisector of
 has length
has length  , where
, where 
- the orthocenter is a reflection of vertex
 over side
over side  .
.
No need to wait until 2026 for twenty six equivalent statements.
Tasks
- (Identical traits) Consider a right triangle
 with side-lengths
with side-lengths  , circumradius
, circumradius  , circumcenter
, circumcenter  , nine-point center
, nine-point center  , and
, and  . Let
. Let  be the circumcenter of
be the circumcenter of  and let
and let  be its circumradius. Similarly, let
be its circumradius. Similarly, let  be the circumcenter of
be the circumcenter of  and let
and let  be its circumradius.
be its circumradius.
- Show that
 are co-linear.
are co-linear. - PROVE that
 and
and  .
. - Deduce that the ratio in which the bisector of
 divides side
divides side  is the same as the circumradii ratio
is the same as the circumradii ratio  .
.
- Show that
- (Identical traits) Consider a non-right triangle
 with side-lengths
with side-lengths  , circumradius
, circumradius  , circumcenter
, circumcenter  , and nine-point center
, and nine-point center  . Let
. Let  be the circumcenter of
be the circumcenter of  and let
and let  be its circumradius. Similarly, let
be its circumradius. Similarly, let  be the circumcenter of
be the circumcenter of  and let
and let  be its circumradius. If
be its circumradius. If  :
:
- Show that
 are co-linear.
are co-linear. - PROVE that
 and
and  .
. - Deduce that the ratio in which the bisector of
 divides side
divides side  is the same as the circumradii ratio
is the same as the circumradii ratio  .
.
(There goes a non-right triangle that mimics a right triangle in many aspects.)
- Show that
- (Isosceles trapezium) Suppose that an obtuse
 satisfies any of the equivalent statements considered in this post. Let
satisfies any of the equivalent statements considered in this post. Let  be a point on the circumcircle such that
be a point on the circumcircle such that  is a diameter.
is a diameter.
- PROVE that
 .
. - Deduce that quadrilateral
 is an isosceles trapezium.
is an isosceles trapezium.
- PROVE that
- (Impossible triangle) In triangle
 , suppose that
, suppose that  and that the length of the median from
and that the length of the median from  is
is  , as per the special case encountered in the course of example 6.
, as per the special case encountered in the course of example 6.
- PROVE that the lengths of sides
 and
and  must be
must be  and
and  (or the other way).
(or the other way). - Using the triangle inequality, deduce that the three points
 are co-linear.
are co-linear.
- PROVE that the lengths of sides
- PROVE that the following two statements are equivalent for any triangle
 :
:

- the length
 of the bisector of
of the bisector of  satisfies
satisfies  .
.