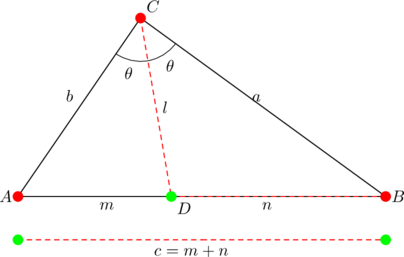
Let ![]() be the side-lengths of
be the side-lengths of ![]() , and let
, and let ![]() be the length of the bisector of
be the length of the bisector of ![]() , as shown below:
, as shown below:
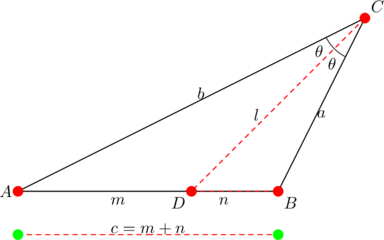
Then ![]() is the geometric mean of
is the geometric mean of ![]() and
and ![]() if, and only if:
if, and only if:
We’ll see the simplifications that result when equation (1) restricts to right triangles
and the simplifications that result when (1) is considered in the context of triangles satisfying
Let’s set the ball rolling with what a right triangle enjoys solely.
Suppose that ![]() is a right triangle with
is a right triangle with ![]() . Then the median from vertex
. Then the median from vertex ![]() is half of the length of the hypotenuse:
is half of the length of the hypotenuse: ![]() and so
and so ![]() is the geometric mean of
is the geometric mean of ![]() and
and ![]() . On the other hand, if a triangle has the property that one of its medians is the geometric mean of the two segments on the opposite side, for example,
. On the other hand, if a triangle has the property that one of its medians is the geometric mean of the two segments on the opposite side, for example, ![]() , we show that the triangle is a right triangle. Indeed:
, we show that the triangle is a right triangle. Indeed:
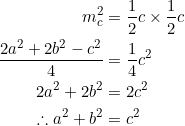
So the triangle is a right triangle. Since all medians are internal, this property is unique to right triangles.
Formula derivation
Our main result is example 4, for which we may need the next two examples.

We first have that ![]() . Also:
. Also:
![]()
The sine rule applied to ![]() s
s ![]() and
and ![]() then gives:
then gives:
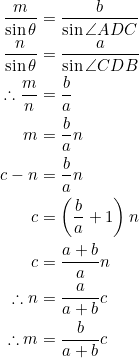
Basically, ![]() . This is very useful in finding the coordinates of the foot of an angle bisector, which in turn is useful in finding the coordinates of the incenter of a triangle.
. This is very useful in finding the coordinates of the foot of an angle bisector, which in turn is useful in finding the coordinates of the incenter of a triangle.
Let’s refer to the diagram in example 2 again:

and then apply Stewart’s theorem to ![]() to obtain
to obtain
![]()
We now use the fact that ![]() and
and ![]() from example 2.
from example 2.
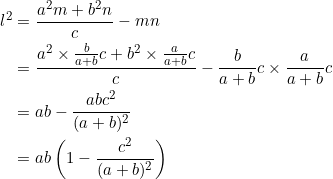
An alternative procedure is to use area arguments as well as the cosine formula and double angle identities for ![]() and
and ![]() . This way one avoids going through Stewart’s theorem and an explicit determination of
. This way one avoids going through Stewart’s theorem and an explicit determination of ![]() and
and ![]() .
.

First suppose that ![]() is the geometric mean of
is the geometric mean of ![]() and
and ![]() . Then
. Then ![]() .
.
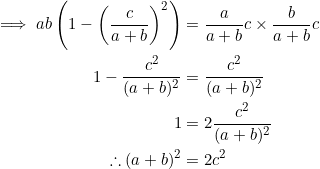
Conversely, suppose that ![]() .
.
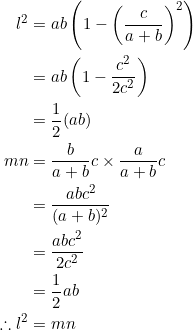
Notice how we obtain another equivalence: ![]() . Translate into words: we killed two birds with one stone.
. Translate into words: we killed two birds with one stone.
The foot ![]() of the bisector of
of the bisector of ![]() has coordinates
has coordinates ![]() . By the distance formula:
. By the distance formula:
![]()
Also:
![]()
Thus, ![]() is the geometric mean of
is the geometric mean of ![]() and
and ![]() .
.
Fifteen degrees
We now restrict equation (1) to right triangles and to triangles satisfying equation (3) . It turns out that the interior angles are all multiples of ![]() .
.
Using the fact that ![]() and
and ![]() , we have:
, we have:
![]()
The angles of the triangle will then be ![]() ,
, ![]() ,
, ![]() . All multiples of
. All multiples of ![]() .
.
In this case ![]() . Together with equation (1), we have
. Together with equation (1), we have
![]()
Alternatively, the bisector is a median in this case, and so the conclusion follows from example 1 and example 4.
We have: ![]() . Isolate
. Isolate ![]() and simplify:
and simplify:
![]()
Since ![]() (see here), we have (by example 7 above):
(see here), we have (by example 7 above):
![]()
Also, ![]() and
and ![]() yield
yield ![]() and
and ![]() (or
(or ![]() and
and ![]() ).
).
Further developments
Here are two out of a few more consequences.
We have ![]() and
and ![]() . Eliminate
. Eliminate ![]() to obtain
to obtain ![]() .
.
In example 4 we had ![]() ; in example 9 above we had
; in example 9 above we had ![]() . Now let’s calculate
. Now let’s calculate ![]() :
:
![]()
We see that ![]() form a geometric progression with common ratio
form a geometric progression with common ratio ![]() .
.
Takeaway
In triangle ![]() , let
, let ![]() be the foot of the bisector of
be the foot of the bisector of ![]() . Then the two statements below are equivalent:
. Then the two statements below are equivalent:
 is the geometric mean of
is the geometric mean of  and
and 
 is the geometric mean of
is the geometric mean of  and
and  .
.
Further, for any triangle ![]() whose side-lengths
whose side-lengths ![]() satisfy equation (1), the following two statements are equivalent:
satisfy equation (1), the following two statements are equivalent:
 is a right triangle
is a right triangle .
.
Finally, for any triangle ![]() whose side-lengths
whose side-lengths ![]() satisfy equation (1), the two statements below are equivalent:
satisfy equation (1), the two statements below are equivalent:
 is a pseudo right triangle
is a pseudo right triangle .
.
Tasks
- Using
 with vertices at
with vertices at  ,
,  ,
,  , verify that:
, verify that:
- its incenter is
 .
. - the ratio of the coordinates
 of the incenter is golden; that is, it satisfies
of the incenter is golden; that is, it satisfies  .
. - the slope of the bisector of
 is
is  , the negative of the golden ratio.
, the negative of the golden ratio.
- its incenter is
- Let
 be the side-lengths of triangle
be the side-lengths of triangle  .
.
- PROVE that the harmonic mean of
 and
and  is
is  .
. - Deduce that the bisector of
 is the harmonic mean of the two segments on the opposite, if
is the harmonic mean of the two segments on the opposite, if  .
.
- PROVE that the harmonic mean of
- Suppose that the side-lengths
 of triangle
of triangle  satisfy equation (3), namely
satisfy equation (3), namely  .
.
- PROVE that the length
 of the bisector of
of the bisector of  satisfies
satisfies  .
. - Deduce that
 is the harmonic mean of
is the harmonic mean of  and
and  .
.
- PROVE that the length
- Suppose that
 satisfies the usual Pythagorean identity
satisfies the usual Pythagorean identity  .
.
- If the bisector of
 satisfies equation (1) adapted as
satisfies equation (1) adapted as  , PROVE that
, PROVE that  .
. - Under the above, deduce that
 ,
,  .
.
- If the bisector of
- In
 , let the side-lengths be
, let the side-lengths be  , and let
, and let  denote the circumradius, altitude from
denote the circumradius, altitude from  , and the length of the bisector of
, and the length of the bisector of  . If
. If  satisfies equation (3), PROVE that the squared lengths
satisfies equation (3), PROVE that the squared lengths  form a geometric progression with common ratio
form a geometric progression with common ratio  .
. - In
 , let
, let  denote the circumradius, altitude from
denote the circumradius, altitude from  , and the median from
, and the median from  . If
. If  satisfies equations (1) and (3), PROVE that
satisfies equations (1) and (3), PROVE that  .
.
(Basically a right triangle can be formed with the median as the hypotenuse.)
as the hypotenuse.)