![]()
Place the vertices of the right triangle at convenient points: ![]() ,
, ![]() , and
, and ![]() . Then:
. Then:
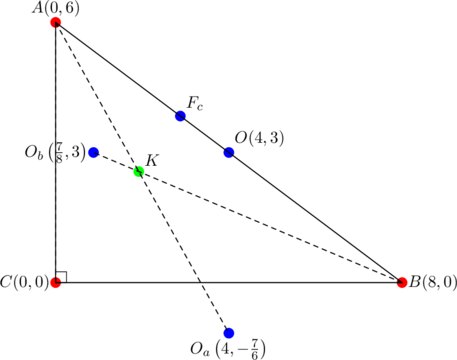
 is the point
is the point  ;
; is the point
is the point  ;
; is the point
is the point  .
.
Using the given coordinates, we find:
![]()
Using the given coordinates, we find:
![]()
Using the given coordinates, we find:
![]()
Follows from
![]()
Follows from
![]()
Takeaway
In any right triangle, the following statements are equivalent:
- the right triangle is isosceles
- the Kosnita point coincides with the centroid.
Task
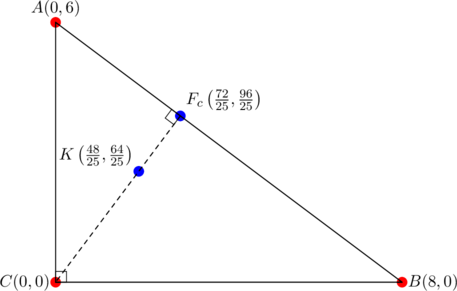
- (Foot of the symmedian) Let
 be a triangle having vertices at
be a triangle having vertices at  ,
,  ,
,  . VERIFY that:
. VERIFY that:
- the foot of the symmedian from
 is
is 
- the foot of the symmedian from
 is equidistant from the feet of the altitudes from
is equidistant from the feet of the altitudes from  and
and  .
.
- the foot of the symmedian from