With that done, we then thought to inaugurate an irregular series on this blog, where we feature our own problems that have been published elsewhere.
Welcome to the first edition of such a series!
Easy problem
The three roots of the cubic ![]() are the slopes of the sides of a triangle. Find the slope of its Euler line. Details here.
are the slopes of the sides of a triangle. Find the slope of its Euler line. Details here.
Among all the proposed problems for that edition, the above was the easiest, as seen from the nature of the question and the number of solutions below.
Editor’s preference
Here’s a screenshot of the editor’s preferred solution:

Extra propositions
A few things to point out in addition to the solution above.
We already saw that the slope of the Euler line of this particular triangle is ![]() from the screenshot above. We show that one side of the triangle has slope
from the screenshot above. We show that one side of the triangle has slope ![]() . Indeed,
. Indeed, ![]() is a root of the cubic equation
is a root of the cubic equation ![]() , since
, since
![]()
So the Euler line is perpendicular to a side of the triangle.
Previously we found ![]() as one of the roots of the cubic equation
as one of the roots of the cubic equation ![]() , and so
, and so ![]() is an associated factor of the cubic. By polynomial division we obtain
is an associated factor of the cubic. By polynomial division we obtain ![]() as the second factor, and so the other two roots can be obtained from the quadratic equation
as the second factor, and so the other two roots can be obtained from the quadratic equation ![]() :
:
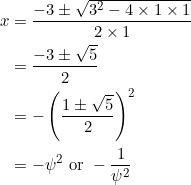
where ![]() is the golden ratio.
is the golden ratio.
The roots are ![]() . They form a geometric progression because
. They form a geometric progression because
![]()
This follows from the fact that the slopes of the sides of the triangle form a geometric progression with ![]() as the geometric mean. (Same result if the geometric mean was
as the geometric mean. (Same result if the geometric mean was ![]() .)
.)
Since the slopes of the sides form a geometric progression with a common ratio ![]() , it follows that the slopes of the medians also form a geometric progression.
, it follows that the slopes of the medians also form a geometric progression.
Takeaway
Let ![]() be a real number. Then the following statements are equivalent:
be a real number. Then the following statements are equivalent:
- the cubic equation
 has (three) real roots
has (three) real roots  or
or  .
.
Tasks
- (Symmetric equations) Consider the cubic equation
 .
.
- Show that
 is always a solution.
is always a solution. - Find a condition on
 for which
for which  is the only real solution.
is the only real solution.
- Show that
- (Social engagement) The problem below was posted on a Facebook group recently:
 Solve it.
Solve it.
 Solve it.
Solve it.