- is on the altitude through the
 -vertex
-vertex - internally divides this altitude in the ratio
 .
.
Construction
Let ![]() be the circumcenter of triangle
be the circumcenter of triangle ![]() . The Kosnita point of
. The Kosnita point of ![]() is constructed as follows:
is constructed as follows:
- find the circumcenter
 of triangle
of triangle  , then join
, then join  to vertex
to vertex 
- find the circumcenter
 of triangle
of triangle  , then join
, then join  to vertex
to vertex 
- find the circumcenter
 of triangle
of triangle  , then join
, then join  to vertex
to vertex 
The lines ![]() ,
, ![]() ,
, ![]() concur at the Kosnita point.
concur at the Kosnita point.
If ![]() is a right triangle in which
is a right triangle in which ![]() , then its circumcenter
, then its circumcenter ![]() is the midpoint of
is the midpoint of ![]() , and so one of the three triangles above is degenerate, namely
, and so one of the three triangles above is degenerate, namely ![]() . To somewhat compensate for this, the Kosnita point in a right triangle behaves nicely.
. To somewhat compensate for this, the Kosnita point in a right triangle behaves nicely.
Calculations
Observe that the given triangle is right-angled at ![]() :
:
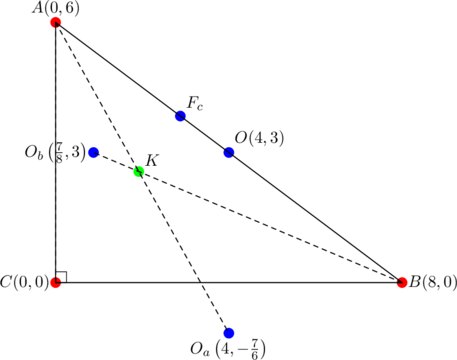
- the circumcenter of
 is
is  , the midpoint of
, the midpoint of 
- the circumcenter of
 is
is  , call this
, call this 
- the circumcenter of
 is
is  , call this
, call this 
- the equation of line
 is
is 
- the equation of line
 is
is 
- the two lines
 and
and  meet at
meet at  .
.
Thus, the Kosnita point of the given triangle is located at ![]() .
.
The same triangle in the previous example:

- the equation of side
 is
is 
- the equation of the altitude through
 is
is 
- thus, the foot of the altitude from
 is
is  .
.
Same triangle as in the previous examples where we obtained ![]() as the Kosnita point.
as the Kosnita point.
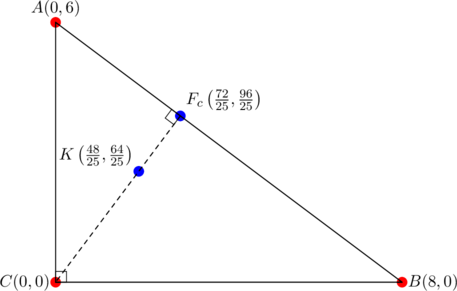
The equation of the altitude through ![]() was obtained in the previous example as
was obtained in the previous example as ![]() . The coordinates of the Kosnita point
. The coordinates of the Kosnita point ![]() satisfy this equation, since
satisfy this equation, since
![]()
and so the Kosnita point lies on the altitude through ![]() .
.
We have ![]() and
and ![]() .
.

Explicit calculation gives ![]() and
and ![]() . Thus
. Thus ![]() .
.
Coordinates
In example 1 we were given ![]() ,
, ![]() , and
, and ![]() . So:
. So: ![]() and
and ![]() . The Kosnita point is then:
. The Kosnita point is then:
![]()
as before.
Caption this:
Takeaway
In any right triangle, the following statements are equivalent:
- the right triangle is isosceles
- the Kosnita point coincides with the centroid.
Task
- (Harmonic division) Let
 be a right triangle having vertices at
be a right triangle having vertices at  ,
,  ,
,  . PROVE that:
. PROVE that:
- the foot of the altitude from
 is
is 
- the symmedian point is

- the Kosnita point is

 and
and  divide
divide  harmonically in the ratio
harmonically in the ratio  .
.
- the foot of the altitude from