This is a paragraph.

Author: Slopefessor Fr1day

A characterization of right triangles II

Recently the following problem was posted on a Facebook group:

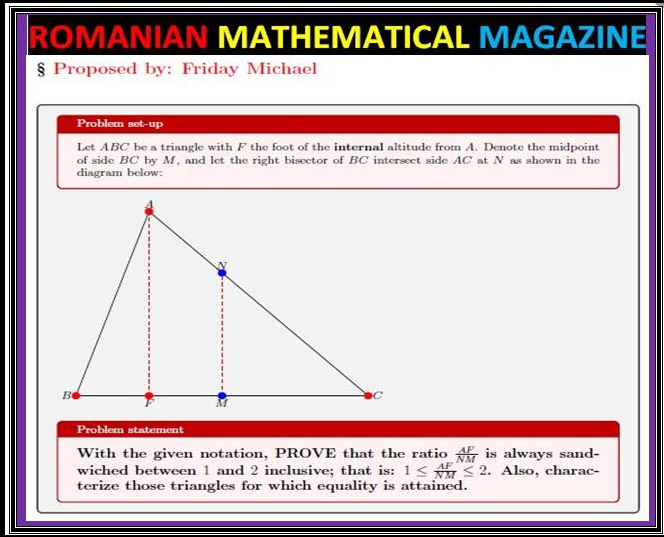
Right now we’ll use this problem to obtain another characterization of right triangles, in addition to the ones here.

Stretched image

To start with, here’s an enlarged version of the above image:

In any triangle, the ratio of the length of an internal altitude to the “length” of a right bisector is always sandwiched between 1 and 2.

Strict inequalities

In general, the ratio under consideration lies strictly between 1 and 2.

In triangle ABC, let F be the foot of the altitude from vertex A and M the midpoint of BC. Suppose that the right bisector of BC intersects side AC at N. If AC> AB, PROVE that: \frac{AF}{MN}=\frac{a^2+b^2-c^2}{a^2}.

Details here.

In triangle ABC, let F be the foot of the altitude from vertex A and M the midpoint of BC. Suppose that the right bisector of BC intersects side AC at N. If AC> AB, PROVE that: \frac{AF}{MN}>1.

Details here.

In triangle ABC, let F be the foot of the altitude from vertex A and M the midpoint of BC. Suppose that the right bisector of BC intersects side AC at N. If AC> AB, PROVE that: \frac{AF}{MN}<2.

Details here.

Together we have: 1<\frac{AF}{MN}<2.

Special instance

When the ratio under consideration equals 2.

Suppose that ABC is a right triangle in which \angle B=90^{\circ} and that M is the midpoint of BC. If the right bisector of BC intersects side AC at N and AC> AB, PROVE that: \frac{AB}{MN}=2.

Use similar triangles. Or else use the fact that: \frac{AF}{NM}=\frac{a^2+b^2-c^2}{a^2} from example 1. Take F=B so that b^2=a^2+c^2. Simplify to get \frac{AB}{MN}=2.

In triangle ABC, let F be the foot of the altitude from vertex A and M the midpoint of BC. Suppose that the right bisector of BC intersects side AC at N. If AC> AB and \frac{AF}{MN}=2, PROVE that ABC is a right triangle with \angle B=90^{\circ}.

Details here.

Takeaway

Let ABC be a triangle in which F is the foot of the internal altitude from vertex A, M is the midpoint of side BC, and the right bisector of BC intersects AC (or AB, depending on which is greater) at N. Then the following statements are equivalent:

  1. ABC is a right triangle in which B=90^{\circ}
  2. \frac{AF}{NM}=2.

Tasks

  • (Silver ratio) Suppose that ABC is a triangle containing an obtuse angle B. Let F be the foot of the altitude from C and let the right bisector of AB intersect AC at N.
    1. PROVE that \frac{CF}{NM}> 2, where M is the midpoint of AB.
    2. Find a triangle for which \frac{CF}{NM}=1+\sqrt{2}, the silver ratio.

Special Edition I: CRUX Problem 4716

Way back in late 2020, we submitted a simple problem to Crux Mathematicorum. After about two years, the problem appeared in the September 2022 edition as Problem 4716, Page 65.

With that done, we then thought to inaugurate an irregular series on this blog, where we feature our own problems that have been published elsewhere.

Welcome to the first edition of such a series!

Easy problem

The three roots of the cubic x^3+4x^2+4x+1=0 are the slopes of the sides of a triangle. Find the slope of its Euler line. Details here.

Among all the proposed problems for that edition, the above was the easiest, as seen from the nature of the question and the number of solutions below.

Editor’s preference

Here’s a screenshot of the editor’s preferred solution:

Extra propositions

A few things to point out in addition to the solution above.

The three roots of the cubic x^3+4x^2+4x+1=0 are the slopes of the sides of a triangle. PROVE that its Euler line is perpendicular to one of the sides.

We already saw that the slope of the Euler line of this particular triangle is 1 from the screenshot above. We show that one side of the triangle has slope -1. Indeed, -1 is a root of the cubic equation x^3+4x^2+4x+1=0, since

    \[(-1)^3+4(-1)^2+4(-1)+1=0\]

So the Euler line is perpendicular to a side of the triangle.

The three roots of the cubic x^3+4x^2+4x+1=0 are the slopes of the sides of a triangle. PROVE that two of the roots are -\psi^2 and -\frac{1}{\psi^2}, where \psi is the golden ratio.

Previously we found -1 as one of the roots of the cubic equation x^3+4x^2+4x+1=0, and so (x+1) is an associated factor of the cubic. By polynomial division we obtain (x^2+3x+1) as the second factor, and so the other two roots can be obtained from the quadratic equation x^2+3x+1=0:

    \begin{equation*} \begin{split} x&=\frac{-3\pm\sqrt{3^2-4\times 1\times 1}}{2\times 1}\\ &=\frac{-3\pm\sqrt{5}}{2}\\ &=-\left(\frac{1\pm\sqrt{5}}{2}\right)^2\\ &=-\psi^2\text{ or }-\frac{1}{\psi^2} \end{split} \end{equation*}

where \psi=\frac{1+\sqrt{5}}{2} is the golden ratio.

The three roots of the cubic x^3+4x^2+4x+1=0 are the slopes of the sides of a triangle. PROVE that the slopes form a geometric progression.

The roots are -1,-\psi^2,-\frac{1}{\psi^2}. They form a geometric progression because

    \[(-1)^2=\left(-\psi^2\right)\times\left(-\frac{1}{\psi^2}\right)\]

The three roots of the cubic x^3+4x^2+4x+1=0 are the slopes of the sides of a triangle. PROVE that the triangle is isosceles.

This follows from the fact that the slopes of the sides of the triangle form a geometric progression with -1 as the geometric mean. (Same result if the geometric mean was 1.)

The three roots of the cubic x^3+4x^2+4x+1=0 are the slopes of the sides of a triangle. PROVE that the slopes of the three medians form a geometric progression.

Since the slopes of the sides form a geometric progression with a common ratio r=\psi^2\neq -2, it follows that the slopes of the medians also form a geometric progression.

Takeaway

Let a be a real number. Then the following statements are equivalent:

  1. the cubic equation x^3+ax^2+ax+1=0 has (three) real roots
  2. a\geq 3 or a\leq -1.

Tasks

  • (Symmetric equations) Consider the cubic equation x^3+ax^2+ax+1=0.
    1. Show that x=-1 is always a solution.
    2. Find a condition on a for which x=-1 is the only real solution.
  • (Social engagement) The problem below was posted on a Facebook group recently:
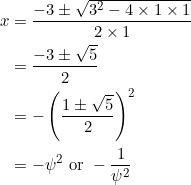
    Solve it.