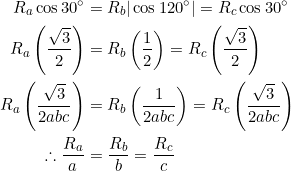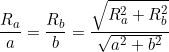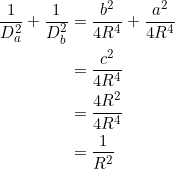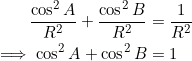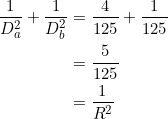Extension confirmed
In one line of equations, the extension that arises from a combination of (1) and (2) is:
(3) ![]()
Please don’t take equation (3) too seriously: there are many relations in Euclidean geometry that can be expressed in terms of the circumradius of a triangle, and equation (3) is just one of them. Meanwhile, note that:
- one of the cosine terms in (2) (or (3)) requires an absolute value if the parent triangle is obtuse
- only right triangles fail some of the equalities in (2) (or (3)).
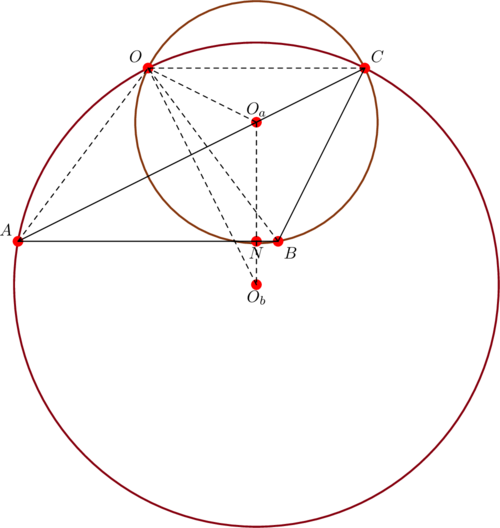
Whether the parent triangle is acute or obtuse, at least one of the associated triangles ![]() has to be obtuse. However, this won’t affect the calculations since all we have to do is use the extended sine law.
has to be obtuse. However, this won’t affect the calculations since all we have to do is use the extended sine law.
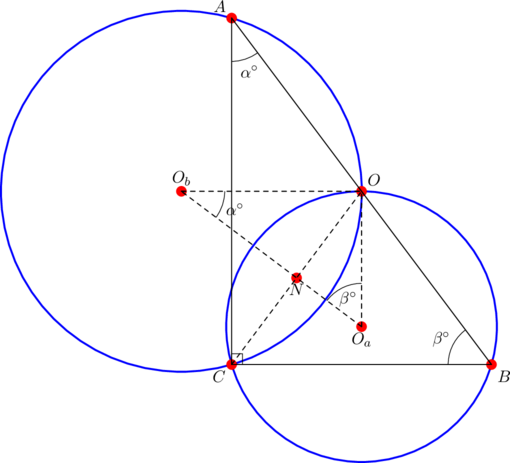
Here ![]() is acute, so it’s circumcenter
is acute, so it’s circumcenter ![]() is located inside the triangle as shown above. Consider
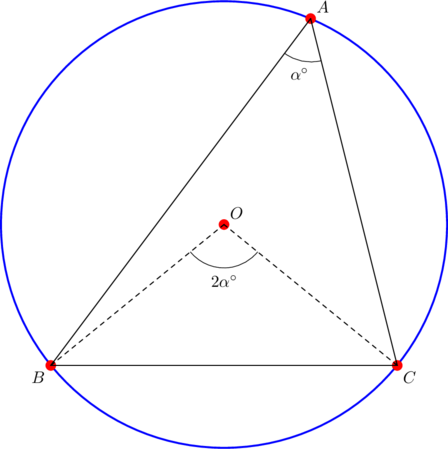
is located inside the triangle as shown above. Consider ![]() . By the inscribed angle theorem, we have:
. By the inscribed angle theorem, we have:
![]()
Now apply the extended sine law to triangle ![]() , noting that
, noting that ![]() :
:
![]()
and so ![]() . In the case where one of the triangles
. In the case where one of the triangles ![]() is obtuse, we also obtain the same result.
is obtuse, we also obtain the same result.
In this case, the circumcenter is located outside the triangle. A sample diagram is shown below:
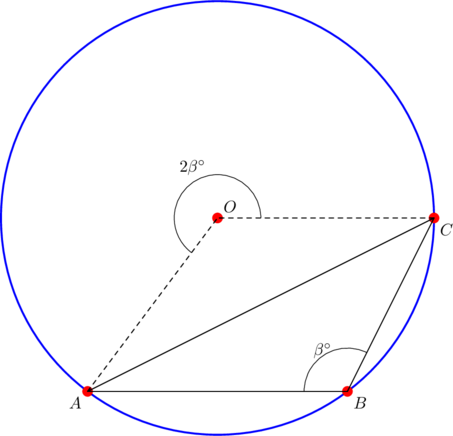
In ![]() , angle
, angle ![]() is equal to
is equal to ![]() , while angles
, while angles ![]() and
and ![]() are both equal to
are both equal to ![]() . Apply the extended sine law again to get:
. Apply the extended sine law again to get:
![]()
This is where an absolute value is needed.
Exception circumvented
If the parent triangle ![]() is right-angled, let’s say at
is right-angled, let’s say at ![]() , then
, then ![]() and so we need modify equation (2) slightly.
and so we need modify equation (2) slightly.
We would have ![]() and
and ![]() . Using equation (2) we have:
. Using equation (2) we have:
![]()
This gives ![]() .
.
Note that since triangle ![]() is right-angled at
is right-angled at ![]() , we have
, we have ![]() . From
. From ![]() isolate
isolate ![]() :
:
![]()
Similarly, ![]() . Together we get
. Together we get ![]() . And
. And
![Rendered by QuickLaTeX.com \[\frac{R_a}{a}=\frac{R_b}{b}=\frac{\sqrt{R_a^2+R_b^2}}{\sqrt{a^2+b^2}}.\]](https://blog.fridaymath.com/wp-content/ql-cache/quicklatex.com-bafc943cc49d2f2a0bfde9dded831557_l3.png)
Exploration continues
We’ll have need to use equation (2) in future. For now, consider what happens in the ![]() isosceles triangle.
isosceles triangle.
Equation changes
An update about our ongoing hide-and-seek game with some hackers. As you can see below, we were initially hoping to use an exponential equation to model their menace, but the data suddenly changed after October 28, and so did our equation.
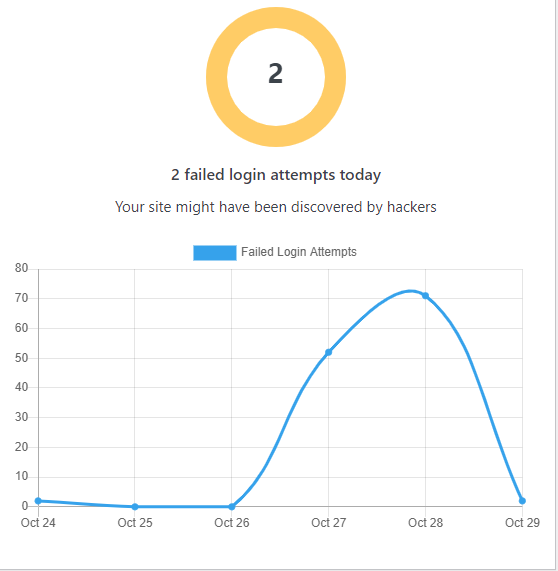
How wonderful would it be if the hackers spent all that time focusing on analytic geometry?
Takeaway
In an obtuse triangle ![]() , let
, let ![]() be as mentioned in the post. Then the following statements are equivalent:
be as mentioned in the post. Then the following statements are equivalent:

 .
.
If instead triangle ![]() is acute, then the following statements are equivalent:
is acute, then the following statements are equivalent:

 .
.
Tasks
- (Similar triangles) Let
 be a non-right triangle with circumcenter
be a non-right triangle with circumcenter  . Denote by
. Denote by  the circumcenters of the triangles
the circumcenters of the triangles  , in that order.
, in that order.
- PROVE that
 is similar to the orthic triangle
is similar to the orthic triangle - Find the similarity ratio.
- PROVE that
- (Similar triangles) Let
 be a right triangle with circumcenter
be a right triangle with circumcenter  and
and  . Denote by
. Denote by  the circumcenters of the triangles
the circumcenters of the triangles  , in that order.
, in that order.
- PROVE that
 is similar to the parent triangle
is similar to the parent triangle 
- Find the similarity ratio.
- PROVE that