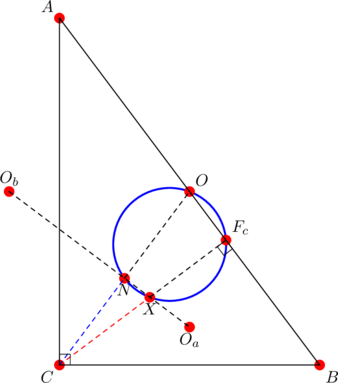
- where a pair of interior opposite angles are both

- with one side and one diagonal having equal lengths.
For today’s purpose, let’s give the pseudonym special to cyclic quadrilaterals having the above two properties, and then prove that in any such special quadrilateral:
Required knowledge
Euler’s quadrilateral formula is the main background needed in order to follow today’s discussion. It’s basically the equation
(2) ![]()
connecting the side-lengths ![]() of a quadrilateral with the diagonals
of a quadrilateral with the diagonals ![]() and the distance
and the distance ![]() between the midpoints of the diagonals.
between the midpoints of the diagonals.
Right kites
In a right kite, equation (2) simplifies to equation (1), that is ![]() , as shown in our first example below.
, as shown in our first example below.
Consider the right kite shown below, with longer diagonal ![]() , and shorter diagonal
, and shorter diagonal ![]() .
.
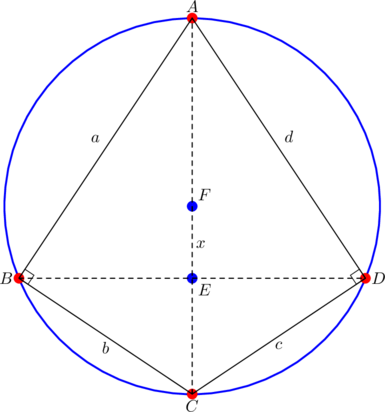
Since ![]() in the kite shown above and
in the kite shown above and ![]() because it’s a right kite, Euler’s quadrilateral formula (2) gives
because it’s a right kite, Euler’s quadrilateral formula (2) gives
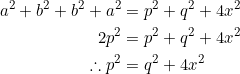
This example shows that apart from right kites, there are other (cyclic) quadrilaterals that satisfy equation (1), including the ones with the pseudonym special, which is our focus for today.
Such a special quadrilateral ![]() contains two interior opposite angles measuring
contains two interior opposite angles measuring ![]() ; place them at
; place them at ![]() and
and ![]() .
.

If we let diagonal ![]() , then
, then ![]() , and so by Euler’s quadrilateral formula (2):
, and so by Euler’s quadrilateral formula (2):
![]()
Using the same diagram/notation for the previous example, we have:
![]()
Since one of the diagonals has the same length as one of the sides, it can’t be diagonal ![]() because
because ![]() is the diameter. So let’s suppose diagonal
is the diameter. So let’s suppose diagonal ![]() as the same length as side
as the same length as side ![]() . Then the above equation gives
. Then the above equation gives ![]() .
.
Rare kind
Diagonal ![]() will now have the same length as sides
will now have the same length as sides ![]() and
and ![]() .
.
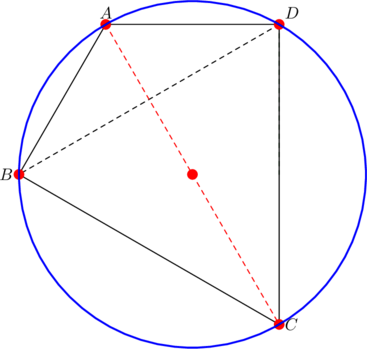
Suppose that ![]() . Let
. Let ![]() and
and ![]() be the circumcenter and orthocenter of the parent triangle
be the circumcenter and orthocenter of the parent triangle ![]() . Then the quadrilateral
. Then the quadrilateral ![]() is a particularly pleasant right kite.
is a particularly pleasant right kite.
Takeaway
Let ![]() be a quadrilateral with side-lengths
be a quadrilateral with side-lengths ![]() , diagonals
, diagonals ![]() , and
, and ![]() the distance between the midpoints of the diagonals. If the interior angles at
the distance between the midpoints of the diagonals. If the interior angles at ![]() and
and ![]() are both
are both ![]() , then the following statements are equivalent:
, then the following statements are equivalent:

 .
.
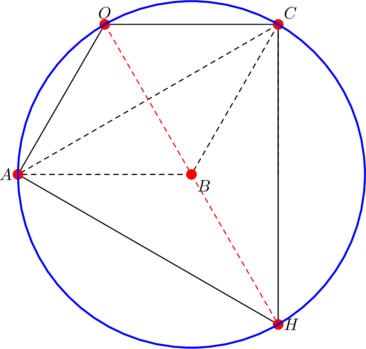
Task
- (Special property) Let
 be special, as per the definition at the introduction; specifically, let the interior opposite angles at
be special, as per the definition at the introduction; specifically, let the interior opposite angles at  and
and  be both
be both  , and let diagonal
, and let diagonal  have the same length as side
have the same length as side  . PROVE that:
. PROVE that:
- the radius through
 is parallel to side
is parallel to side 
- the orthocenter of triangle
 is a reflection of vertex
is a reflection of vertex  over side
over side  .
.
- the radius through