A special cyclic quadrilateral I – High School Geometry

The class of cyclic quadrilaterals to be considered in this (and possibly next) post:

can be built from any non-isosceles right triangle
contain a pair of $90^{\circ}$ angles facing each other
combine some properties of right kites with some properties of quasi-harmonic quadrilaterals.

Thus, they are special.

Partial proofs

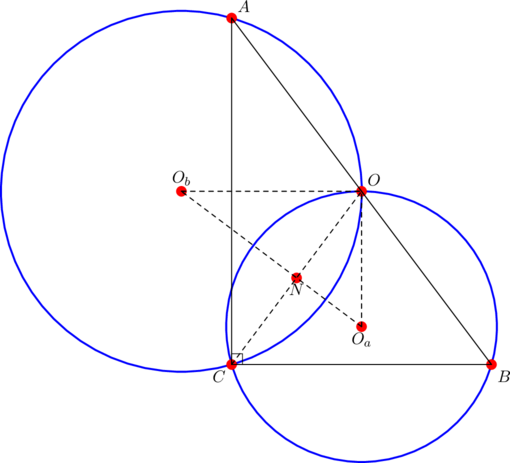
Throughout we work with a non-isosceles right triangle $ABC$ in which $\angle C=90^{\circ}$ . $O$ and $N$ denote the circumcenter and nine-point center.

Explain how to construct a cyclic quadrilateral that exhibits the properties hinted at above.

To see a basic construction of such a cyclic quadrilateral, take any non-isosceles right triangle $ABC$ in which $\angle C=90^{\circ}$ . Denote its circumcenter by $O$ , its nine-point center by $N$ , and its circumradius by $R$ . Consider triangles $AOC$ and $BOC$ with circumcenters $O_b$ and $O_a$ . Let the segment $O_aO_b$ intersect the altitude from $C$ at point $X$ . Then the quadrilateral $ONXF_c$ , with $F_c$ the foot of the altitude from $C$ , is cyclic.

Suppose that the segment $O_aO_b$

intersects the altitude through $C$

at point $X$

. PROVE that $ONXF_c$

is a cyclic quadrilateral.

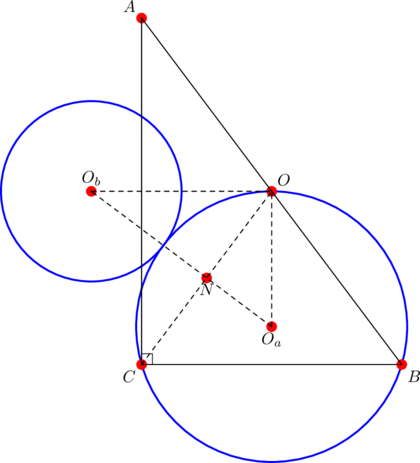
Consider the convex quadrilateral $ONXF_c$ in the diagram below:

The interior angles at $N$ and $F_c$ are both $90^{\circ}$ , while the interior angles at $X$ and $O$ are $2\angle B$ and $180^{\circ}-2\angle B$ .

In the cyclic quadrilateral $ONXF_c$

above, explain why the parent right triangle $ABC$

should be non-isosceles.

If the parent triangle is isosceles, the altitude $CF_c$ coincides with the median $CO$ , in which case $ONXF_c$ is just a line.

In the cyclic quadrilateral $ONXF_c$

above, PROVE that one side and one diagonal are equal.

Indeed, $ON=NF_c$ , and both are equal to $R/2$ , where $R$ is the circumradius of the parent triangle $ABC$ .

Let $O_b$

and $O_a$

denote the circumcenters of triangles $AOC$

and $BOC$

. PROVE that $O_b,N,O_a$

are co-linear.

Since $\angle C=90^{\circ}$ as stated, the nine-point center $N$ is the midpoint of segment $CO$ . Triangles $AOC$ and $BOC$ both contain the segment $CO$ . Thus $O_b,N,O_a$ are co-linear because they all lie on the right bisector of $CO$ .

Takeaway

Let $ABC$ be an acute triangle with circumcenter $O$ and circumradius $R$ . Further, let $D_a$ and $D_b$ be the diameters of the circumcircles of $BOC$ and $AOC$ . Then the following statements are equivalent:

$ABC$ is a right triangle in which $\angle C=90^{\circ}$
the identity $\frac{1}{R^2}=\frac{1}{D_a^2}+\frac{1}{D_b^2}$ holds.

In case the parent triangle $ABC$ is obtuse, we have the following analogous equivalence:

the side-lengths $a,b,c$ satisfy $(b^2-a^2)^2=(ac)^2+(cb)^2$
the identity $\frac{1}{R^2}=\frac{1}{D_a^2}+\frac{1}{D_b^2}$ holds.

Task

(Inverted squares) Let be a right triangle in which , the circumcenter is , and the circumradius is . PROVE that:
1. the diameters $D_b$ and $D_a$ of the circles $AOC$ and $BOC$ are related to $R$ via an inverted Pythagorean identity:
  
  (1) $\begin{equation*} \frac{1}{D_a^2}+\frac{1}{D_b^2}=\frac{1}{R^2} \end{equation*}$
  
  (The relation in (1) also holds when the parent right triangle is isosceles, but the quadrilateral $ONXF_c$ degenerates in that case. More on this later.)
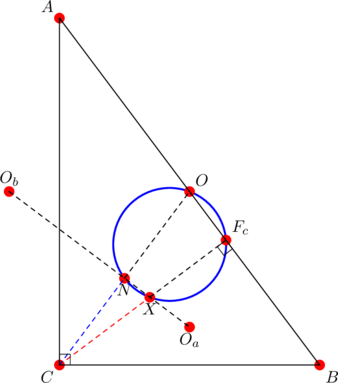
(Impossible situation) Let be a right triangle in which , and let and be as in the discussion.
1. Find a condition under which a circle centred at $O_b$ will be externally tangent to the circle $BOC$ as in the diagram
2. PROVE that if the circumcircles of $AOC$ and $BOC$ touch externally, then $c=a+b$ .
3. Deduce that it is impossible for the circumcircles of $AOC$ and $BOC$ to touch externally.