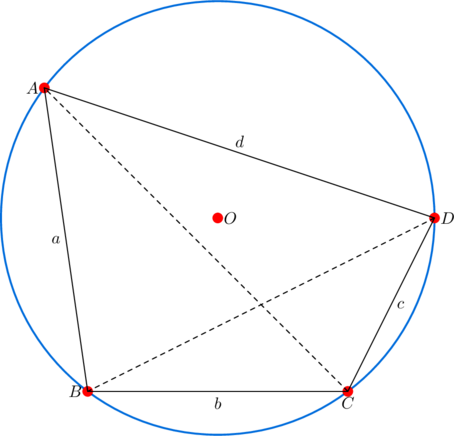
However, instead of requiring that the products of opposite sides are equal, we can stipulate that the products of consecutive sides are equal, and then call the resulting cyclic quadrilateral quasi harmonic.
Having this latter requirement (e.g. ![]() in the diagram below) yields some nice lateral properties for quadrilaterals that satisfy them.
in the diagram below) yields some nice lateral properties for quadrilaterals that satisfy them.
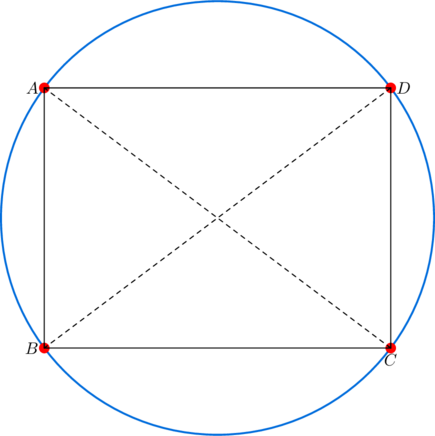
Any rectangle can be inscribed in a circle, and the products of consecutive sides are equal (e.g. ![]() below). Thus, rectangles are quasi-harmonic as per our definition. Note that a rectangle is not a harmonic quadrilateral, unless the rectangle is square.
below). Thus, rectangles are quasi-harmonic as per our definition. Note that a rectangle is not a harmonic quadrilateral, unless the rectangle is square.
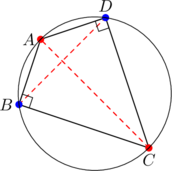
Right kites are both harmonic and quasi-harmonic. So are squares.
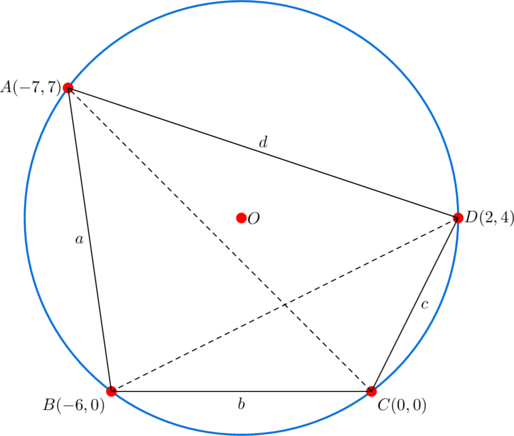
We need to show that it’s cyclic, and that the products of the lengths of consecutive sides are equal.
- side-lengths:
 ,
,  ,
,  ,
, 
- diagonals:
 ,
, 
- Ptolemy’s theorem:
 , and
, and  . Confirms
. Confirms  is cyclic.
is cyclic. - product of consecutive sides:
 . Quasi harmonic.
. Quasi harmonic.
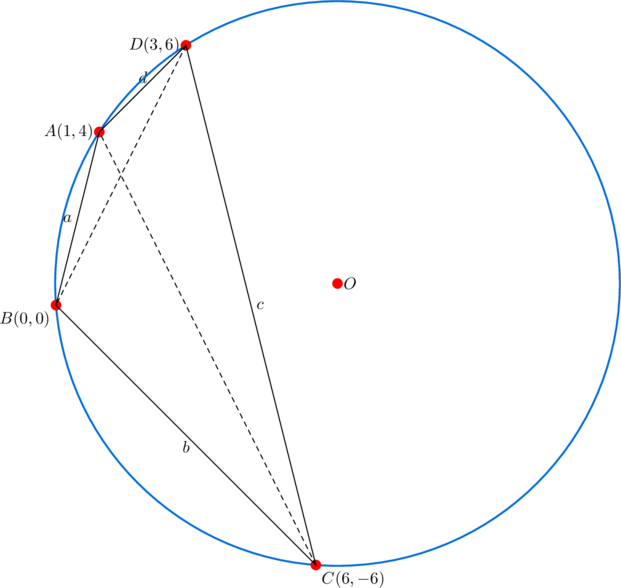
- side-lengths:
 ,
,  ,
,  ,
, 
- diagonals:
 ,
, 
- Ptolemy’s theorem:
 , and
, and  . Confirms
. Confirms  is cyclic.
is cyclic. - product of consecutive sides:
 . Quasi harmonic.
. Quasi harmonic.
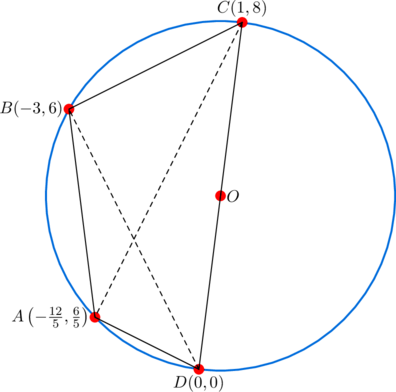
- side-lengths:
 ,
,  ,
,  ,
, 
- diagonals:
 ,
, 
- Ptolemy’s theorem:
 , and
, and  . Confirms
. Confirms  is cyclic.
is cyclic. - product of consecutive sides:
 . Quasi harmonic.
. Quasi harmonic.
Takeaway
Let ![]() be a convex cyclic quadrilateral with side-lengths
be a convex cyclic quadrilateral with side-lengths ![]() ,
, ![]() ,
, ![]() , and
, and ![]() . Then the following statements are equivalent:
. Then the following statements are equivalent:

- diagonal
 bisects diagonal
bisects diagonal  .
.
The longer diagonal in a quasi harmonic quadrilateral always bisects the shorter diagonal.
Task
- (Bisection condition) Let
 be a convex cyclic quadrilateral with side-lengths
be a convex cyclic quadrilateral with side-lengths  ,
,  ,
,  , and
, and  . PROVE that:
. PROVE that:
- diagonal
 bisects diagonal
bisects diagonal  if and only if
if and only if 
- diagonal
 bisects diagonal
bisects diagonal  if and only if
if and only if 
- diagonals
 and
and  bisect each other if and only if
bisect each other if and only if  and
and  (rectangle).
(rectangle).
- diagonal
- (Basic characteristics) Let
 be a convex cyclic quadrilateral in which the side-lengths are
be a convex cyclic quadrilateral in which the side-lengths are  ,
,  ,
,  ,
,  , and the diagonals are
, and the diagonals are  ,
,  . If
. If  (quasi-harmonic), PROVE that:
(quasi-harmonic), PROVE that:

-
 .
.