Consequently, the bisection condition to be established in today’s post applies only to convex quadrilaterals — quadrilaterals where none of the interior angles exceed ![]() .
.
Concave quadrilaterals also exist, but we won’t cover those.
Check how many attacks we faced this week! Cause for concern? 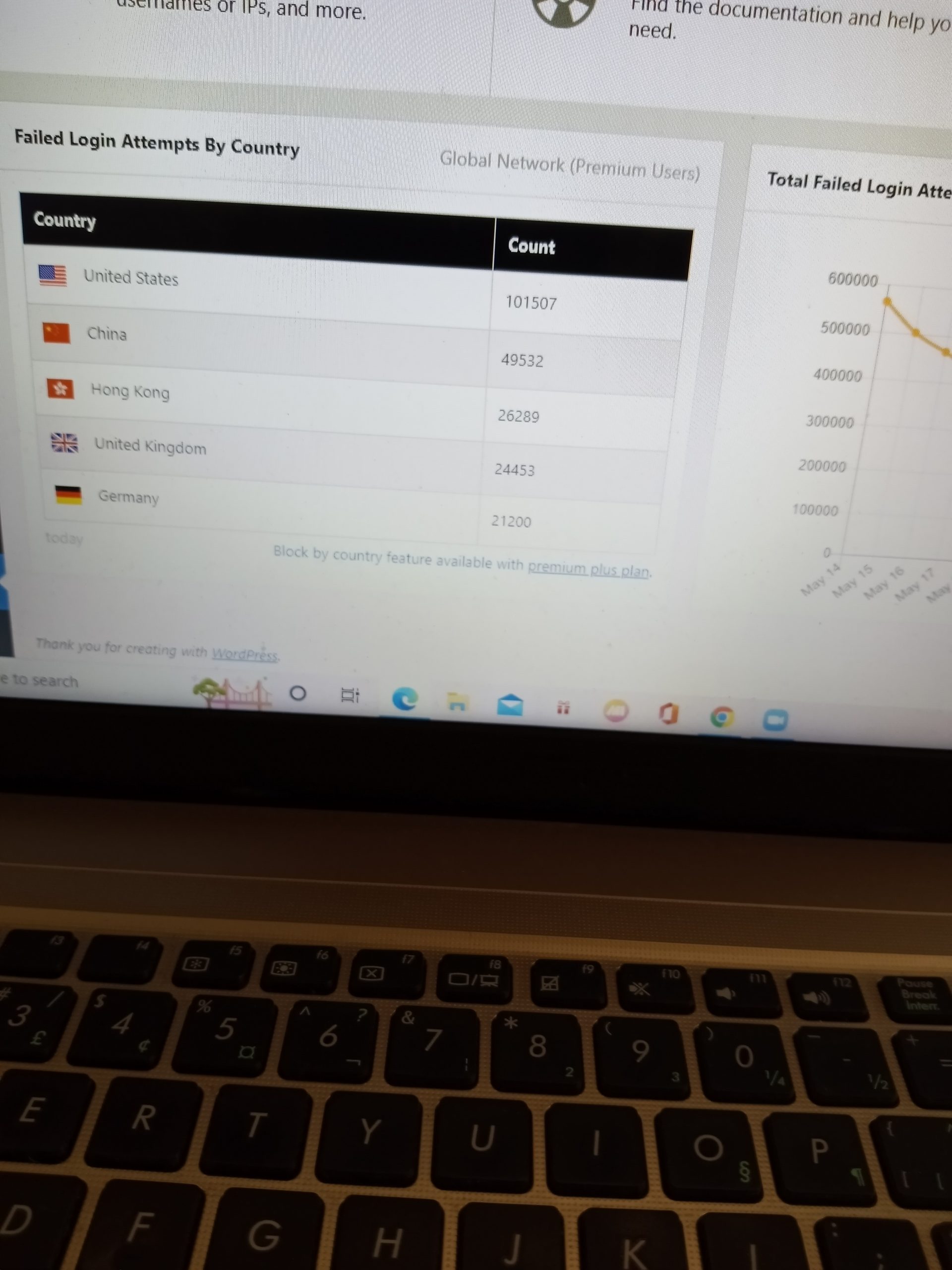
As usual, ![]() are the side-lengths
are the side-lengths ![]() . Assume for the time being that none of these sides are equal.
. Assume for the time being that none of these sides are equal.
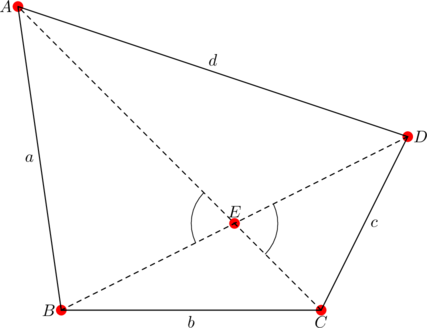
Let the length of diagonal ![]() be
be ![]() . Since
. Since ![]() bisects
bisects ![]() , both
, both ![]() and
and ![]() are medians in triangles
are medians in triangles ![]() and
and ![]() , respectively. Thus:
, respectively. Thus:
![]()
The angles ![]() and
and ![]() are equal, so:
are equal, so:
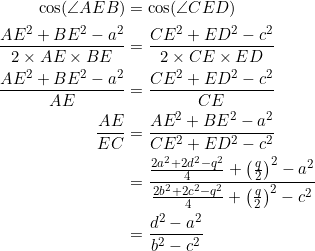
We later realized that applying Stewart’s theorem would have made the proof simpler. Same with the converse in example 2 below.
To this end, consider the four triangles ![]() ,
, ![]() ,
, ![]() , and
, and ![]() . For simplicity let’s set
. For simplicity let’s set
![]()
Thus the assumption ![]() can then be re-written as
can then be re-written as ![]() , or
, or ![]() . The angles
. The angles ![]() and
and ![]() are supplementary, so:
are supplementary, so:
![Rendered by QuickLaTeX.com \begin{align*} \cos(\angle AEB)&=-\cos(\angle(BEC)\\ \implies\frac{AE^2+BE^2-AB^2}{2\times AE\times BE}&=-\left(\frac{BE^2+EC^2-BC^2}{2\times BE\times EC}\right)\\ \implies \frac{p_1^2+q_1^2-a^2}{2p_1q_1}&=-\left(\frac{q_1^2+p_2^2-b^2}{2q_1p_2}\right)\\ p_2(p_1^2+q_1^2-a^2)&=-p_1(q_1^2+p_2^2-b^2)\\ (p_1+p_2)q_1^2&=b^2p_1+a^2p_2-p_1p_2^2-p_1^2p_2\\ &=b^2\left[\left(\frac{d^2-a^2}{b^2-c^2}\right)p_2\right]+a^2p_2-p_1p_2(p_1+p_2)\\ &=\left(\frac{b^2d^2-a^2c^2}{b^2-c^2}\right)p_2-p_1p_2(p_1+p_2)\\ \therefore q_1^2&=\frac{p_2}{p_1+p_2}\left(\frac{b^2d^2-a^2c^2}{b^2-c^2}\right)-p_1p_2 \end{align*}](https://blog.fridaymath.com/wp-content/ql-cache/quicklatex.com-3e02c7ef543794bef7a157f9754fb421_l3.png)
Similarly, the angles ![]() and
and ![]() are supplementary; so:
are supplementary; so:
![Rendered by QuickLaTeX.com \begin{align*} \cos(\angle CED)&=-\cos(\angle AED)\\ \implies \frac{ED^2+EC^2-CD^2}{2\times ED\times EC}&=-\left(\frac{AE^2+ED^2-DA^2}{2\times AE\times ED}\right)\\ \frac{q_2^2+p_2^2-c^2}{2q_2p_2}&=-\left(\frac{p_1^2+q_2^2-d^2}{2p_1q_2}\right)\\ p_1(q_2^2+p_2^2-c^2)&=-p_2(p_1^2+q_2^2-d^2)\\ (p_1+p_2)q_2^2&=c^2p_1+d^2p_2-p_1p_2^2-p_2p_1^2\\ &=c^2\left[\left(\frac{d^2-a^2}{b^2-c^2}\right)p_2\right]+d^2p_2-p_1p_2(p_1+p_2)\\ &=\left(\frac{b^2d^2-a^2c^2}{b^2-c^2}\right)p_2-p_1p_2(p_1+p_2)\\ \therefore q_2^2&=\frac{p_2}{p_1+p_2}\left(\frac{b^2d^2-a^2c^2}{b^2-c^2}\right)-p_1p_2 \end{align*}](https://blog.fridaymath.com/wp-content/ql-cache/quicklatex.com-117f44a9be46ee032ff32c0b2c8f0b69_l3.png)
The preceding calculation shows that ![]() , or
, or ![]() . Thus
. Thus ![]() and the diagonal
and the diagonal ![]() is bisected as desired.
is bisected as desired.
For parallelograms, opposite sides are equal, so we can set ![]() and
and ![]() and obtain
and obtain ![]() . For squares and rhombuses, we need to take care: pretend that
. For squares and rhombuses, we need to take care: pretend that ![]() and
and ![]() are different, and that
are different, and that ![]() and
and ![]() are also different; at the same time, use the fact that opposite sides are equal. Doing this gives
are also different; at the same time, use the fact that opposite sides are equal. Doing this gives ![]() .
.
This is a special case because ![]() and
and ![]() and opposite sides are not equal in general kites. So we’re confronted with the indeterminate form
and opposite sides are not equal in general kites. So we’re confronted with the indeterminate form ![]() . However, the longer diagonal in a kite can be as long as possible, and so the ratio
. However, the longer diagonal in a kite can be as long as possible, and so the ratio ![]() evaluates differently depending on the kite in question. Does this somehow explain why
evaluates differently depending on the kite in question. Does this somehow explain why ![]() is said to be undefined?
is said to be undefined?
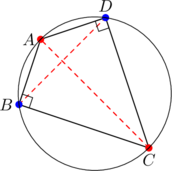
Let ![]() be the point of intersection of
be the point of intersection of ![]() and
and ![]() . Since
. Since ![]() , triangle
, triangle ![]() is isosceles, and so
is isosceles, and so ![]() is an altitude. Thus
is an altitude. Thus ![]() is also an altitude. Since
is also an altitude. Since ![]() , this forces
, this forces ![]() . So we obtain a kite.
. So we obtain a kite.
Takeaway
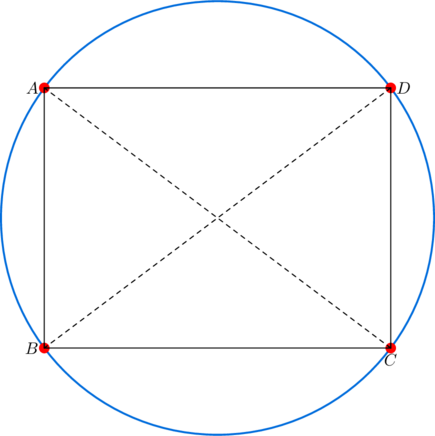
Let ![]() be a convex cyclic quadrilateral whose diagonals
be a convex cyclic quadrilateral whose diagonals ![]() and
and ![]() intersect at
intersect at ![]() . If the side-lengths are
. If the side-lengths are ![]() ,
, ![]() ,
, ![]() , and
, and ![]() , then the following statements are equivalent:
, then the following statements are equivalent:



 bisects
bisects  .
.
Notice the second and third statements.
Task
- (Bisection consequence) Let
 be a convex quadrilateral with side-lengths
be a convex quadrilateral with side-lengths  ,
,  ,
,  , and
, and  . If
. If  bisects
bisects  and
and  (quasi-harmonic), PROVE that
(quasi-harmonic), PROVE that  is cyclic.
is cyclic. - (Basic characteristics) Let
 be a convex cyclic quadrilateral whose diagonals
be a convex cyclic quadrilateral whose diagonals  and
and  intersect at
intersect at  . If
. If  (quasi-harmonic), PROVE that:
(quasi-harmonic), PROVE that:

-
 .
.