The silver ratio and a polar circle

Numerically, the silver ratio is equal to $1+\sqrt{2}$

, and may be denoted by $\delta_s$

Next, a polar circle is a circle centred at the orthocenter of a triangle, with radius $r$ related to the circumradius $R$ and the side-lengths $a,b,c$ via

(1) $\begin{equation*} \begin{split} r^2&=4R^2-\frac{1}{2}\left(a^2+b^2+c^2\right) \end{split} \end{equation*}$

Now suppose that $a,b,c$ satisfy the identity:

(2) $\begin{equation*} \begin{split} (a^2-b^2)^2&=(ac)^2+(cb)^2 \end{split} \end{equation*}$

Notice that any triangle in which equation (2) holds is necessarily obtuse, and so it’s polar circle is defined, with equation (1) simplifying to:

(3) $\begin{equation*} \begin{split} r^2&=\frac{1}{2}\left(a^2+b^2-c^2\right) \end{split} \end{equation*}$

Not only this, it happens that $r=R$ precisely when $\frac{a}{b}$ is the silver ratio.

Reduced attacks

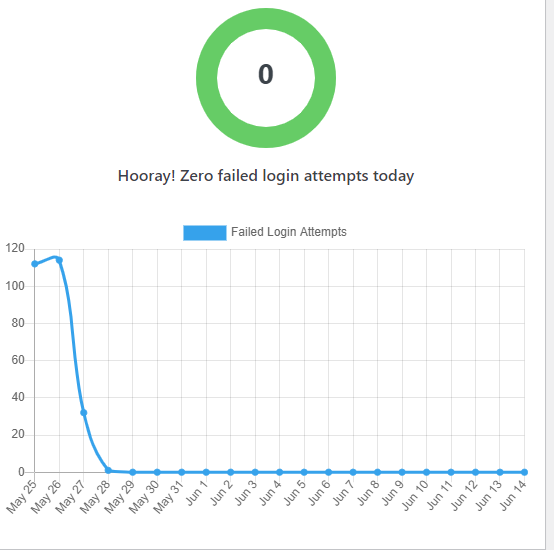
A little bit of our private life before we proceed to something less irrelevant: We’re so glad that, as it stands, we have the upper hand in our fight against unwanted attacks:

The barrage was quite something prior to two weeks ago:

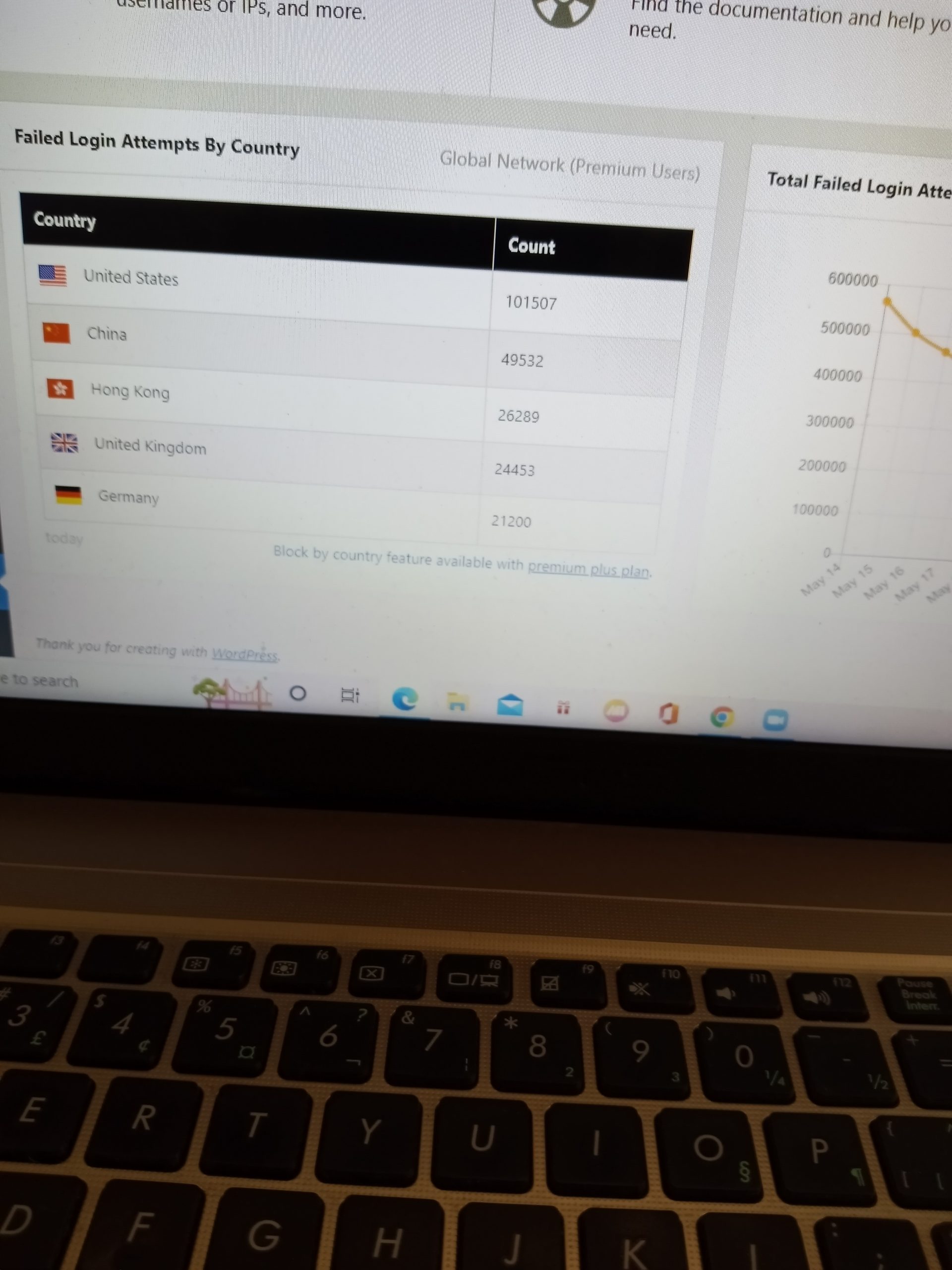
Grateful to find a barricade. It’s a different story now.

Refocused attention

Sorry we had to bother you with the above. Once in a while we’ll let you see what happens behind our scenes.

If the side-lengths $a,b,c$

of $\triangle ABC$

satisfy equation (2), PROVE that the radius of its polar circle satisfies equation (3).

We’re to show that if $(a^2-b^2)^2=(ac)^2+(cb)^2$ , then the radius of the polar circle is $r^2=\frac{1}{2}\left(a^2+b^2-c^2\right)$ . Use the fact that in a non-right triangle, we have $(a^2-b^2)^2=(ac)^2+(cb)^2\iff a^2+b^2=4R^2$ .

Suppose that $(a^2-b^2)^2=(ac)^2+(cb)^2$

, and that the radius of the polar circle coincides with the circumradius. PROVE that $\frac{a}{b}$

is the silver ratio.

We had $r^2=\frac{1}{2}\left(a^2+b^2-c^2\right)$ from the preceding example. And also $R^2=\frac{a^2+b^2}{4}$ . If we set $r^2=R^2$ we get $a^2+b^2=2c^2$ after some simplification. In addition, $c^2=\frac{(a^2-b^2)^2}{a^2+b^2}$ . Thus: $a^2+b^2=2\left(\frac{(a^2-b^2)^2}{a^2+b^2}\right)$ . Further simplification: $a^4-6a^2b^2+b^4=0\implies\left(\frac{a}{b}\right)^2=(1\pm \sqrt{2})^2$ . Take the positive value: $\frac{a}{b}=1+\sqrt{2}$ , the silver ratio.

If $\frac{a}{b}$

is the silver ratio and $(a^2-b^2)^2=(ac)^2+(cb)^2$

, PROVE that the radius of the polar circle coincides with the circumradius.

Similar to the preceding example.

Determine the value of $\angle C$

under the conditions $\frac{a}{b}=1+\sqrt{2}$

and $(a^2-b^2)^2=(ac)^2+(cb)^2$

We had $a^2+b^2=2c^2$ . Since $\frac{a}{b}=1+\sqrt{2}$ , we then obtain $c^2=\sqrt{2}ab$ . Cosine formula: $\cos C=\frac{a^2+b^2-c^2}{2ab}=\frac{2c^2-c^2}{2\left(\frac{c^2}{\sqrt{2}}\right)}=\frac{\sqrt{2}}{2}\implies C=45^{\circ}$ .

Radical axis

Under the conditions $\frac{a}{b}=1+\sqrt{2}$

and $(a^2-b^2)^2=(ac)^2+(cb)^2$

, show that the radical axis of the circumcircle and the polar circle goes through the nine-point center.

Both the circumcircle and the polar circle have the same radius, under the given conditions. Thus the radical axis is the right bisector of the line joining their centers. But then the center of one is the circumcenter, while the center of the other is the orthocenter. The midpoint of these two centers is the nine-point center.

Takeaway

Suppose that triangle $ABC$ has side-lengths $a,b,c$ , radius of polar circle $r$ , and circumradius $R$ . If $(a^2-b^2)^2=(ac)^2+(cb)^2$ , then the following statements are equivalent:

$r=R$
$\frac{a}{b}$ is the silver ratio.

Tasks

(Geometric mean) Suppose that the side-lengths of satisfy . PROVE that the following statements are equivalent:
1. $\frac{a}{b}$ is the silver ratio
2. the nine-point center coincides with the foot of the symmedian from vertex $C$
3. the radius of the nine-point circle is the geometric mean of the two segments into which the nine-point center divides side $AB$ .
(Growing membership) In a non-right triangle , let be the side-lengths, the altitudes, the feet of the altitudes from the respective vertices, the midpoints of sides in that order, the Euler points, the circumradius, the circumcenter, the nine-point center, the orthocenter, the reflection of over side , the reflection of over side , the reflection of over side , the symmedian point, the foot of the symmedian from vertex , and the radius of the polar circle. PROVE that the following eighty-three statements are equivalent:
1. $E_c=F_c$
2. $AH=b$
3. $BH=a$
4. $AE_a=\frac{b}{2}$
5. $BE_b=\frac{a}{2}$
6. $E_aM_c=\frac{a}{2}$
7. $E_bM_c=\frac{b}{2}$
8. $E_aM_b=h_c$
9. $E_aF_b=\frac{AH}{2}$
10. $E_bF_a=\frac{BH}{2}$
11. $OO^a=b$
12. $OO^b=a$
13. $OM_a=\frac{b}{2}$
14. $OM_b=\frac{a}{2}$
15. $OM_c=h_c$
16. $CH=2h_c$
17. $h_a=AF_b$
18. $h_b=BF_a$
19. $AF_c=\frac{b^2}{2R}$
20. $BF_c=\frac{a^2}{2R}$
21. $\frac{a}{c} =\frac{h_c}{AF_b}$
22. $\frac{b}{c}=\frac{h_c}{BF_a}$
23. $\frac{a}{b}=\frac{BF_a}{AF_b}$
24. $R=\frac{b^2-a^2}{2c}$
25. $\frac{CK}{KK_c}=\left(\frac{a^2+b^2}{a^2-b^2}\right)^2$
26. $r^2=\frac{1}{2}\left(a^2+b^2-c^2\right)$
27. $h_c=R\cos C$
28. $\cos A=\frac{b}{\sqrt{a^2+b^2}}$
29. $\cos B=-\frac{a}{\sqrt{a^2+b^2}}$
30. $\cos C=\frac{2ab}{a^2+b^2}$
31. $\sin A=\frac{a}{\sqrt{a^2+b^2}}$
32. $\sin B=\frac{b}{\sqrt{a^2+b^2}}$
33. $\sin C=\frac{b^2-a^2}{a^2+b^2}$
34. $\cos^2 A+\cos^2 B=1$
35. $\sin^2 A+\sin^2 B=1$
36. $a\cos A+b\cos B=0$
37. $\sin A+\cos B=0$
38. $\cos A-\sin B=0$
39. $2\cos A\cos B+\cos C=0$
40. $2\sin A\sin B-\cos C=0$
41. $\cos A\cos B+\sin A\sin B=0$
42. $a\cos A-b\cos B=\sqrt{a^2+b^2}\cos C$
43. $\sin A\sin B=\frac{ab}{b^2-a^2}\sin C$
44. $\sin^2B-\sin^2A=\sin C$
45. $\cos^2A-\cos^2B=\sin C$
46. $OH^2=5R^2-c^2$
47. $h_a^2+h_b^2=AB^2$
48. $\frac{h_a}{a}+\frac{h_b}{b}=\frac{c}{h_c}$
49. $a^2+b^2=4R^2$
50. $b=2R\cos A$
51. $A-B=\pm 90^{\circ}$
52. $(a^2-b^2)^2=(ac)^2+(cb)^2$
53. $AH^2+BH^2+CH^2=8R^2-c^2$
54. $\left(c+2AF_c\right)^2=a^2+b^2$ or $\left(c+2BF_c\right)^2=a^2+b^2$
55. $E_a$ is the reflection of $M_b$ over side $AB$
56. $E_b$ is the reflection of $M_a$ over side $AB$
57. $\triangle ABH$ is congruent to $\triangle ABC$
58. $\triangle OO^aO^b$ is congruent to $\triangle ABC$
59. $\triangle CNO$ is isosceles with $CN=NO$
60. $\triangle CNH$ is isosceles with $CN=NH$
61. $\triangle CHO$ is right angled at $C$
62. $N$ is the circumcenter of $\triangle CHO$
63. $\triangle O^cOC$ is right-angled at $O$
64. $\triangle O^cHC$ is right-angled at $H$
65. quadrilateral $O^cOHC$ is a rectangle
66. the points $O^c,O,C,H$ are concyclic with $OH$ as diameter
67. the reflection $O^b$ of $O$ over $AC$ lies internally on $AB$
68. the reflection $O^a$ of $O$ over $BC$ lies externally on $AB$
69. radius $OC$ is parallel to side $AB$
70. $F_a$ is the reflection of $F_b$ over side $AB$
71. segment $F_aF_b$ is perpendicular to side $AB$
72. the nine-point center lies on $AB$
73. the orthic triangle is isosceles with $F_aF_c=F_bF_c$
74. the geometric mean theorem holds
75. the bisector of $\angle C$ has length $l$ , where $l^2=\frac{2a^2b^2}{a^2+b^2}$
76. the orthocenter is a reflection of vertex $C$ over side $AB$
77. segment $HC$ is tangent to the circumcircle at point $C$
78. median $CM_c$ has the same length as the segment $HM_c$
79. the bisector $M_cO$ of $AB$ is tangent to the nine-point circle at $M_c$
80. $AF_aBF_b$ is a convex kite with diagonals $AB$ and $F_aF_b$
81. altitude $CF_c$ is tangent to the nine-point circle at $F_c$
82. chord $F_cM_c$ is a diameter of the nine-point circle
83. segment $HF_c$ is tangent to the nine-point circle at $F_c$ .
  (Five more members were recently added.)