(1) ![]()
that can be used to characterize right triangles.
To this end, let ![]() be a right triangle in which
be a right triangle in which ![]() , and
, and
 the circumcenter
the circumcenter the circumradius
the circumradius and
and  the diameters of triangles
the diameters of triangles  and
and  .
.
Then equation (1) holds.
Preliminary calculations
A sample diagram is shown below:
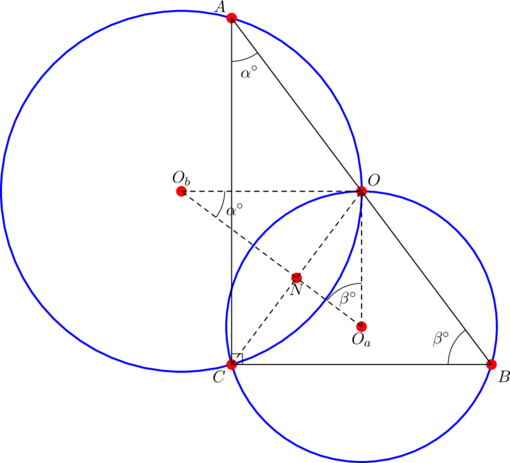
Since ![]() is the circumcenter of
is the circumcenter of ![]() , it lies somewhere on the right bisector of side
, it lies somewhere on the right bisector of side ![]() and so when
and so when ![]() is joined to
is joined to ![]() , the segment
, the segment ![]() is then parallel to side
is then parallel to side ![]() . Similarly,
. Similarly, ![]() is parallel to side
is parallel to side ![]() . Thus
. Thus ![]() . Now join
. Now join ![]() to
to ![]() and use angle chasing to complete the similarity argument.
and use angle chasing to complete the similarity argument.
From the previous example, we saw the similarity between triangle ![]() and the parent triangle
and the parent triangle ![]() :
:

So:
![]()
We obtain ![]() as required. Notice also that we have
as required. Notice also that we have
(2) 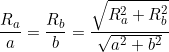
Partial characterization
Partial in the sense that there’s another triangle for which the equivalence in the next two examples works. We’ll see that later.
Apply the extended sine law to triangle ![]() below, noting that
below, noting that ![]() :
:

This would give:
![]()
Similarly, applying the extended sine law to triangle ![]() gives
gives
![]()
Since ![]() and
and ![]() , we now get:
, we now get:
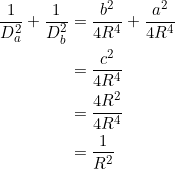
We’ll show in a later post that the following extension of the extended sine law holds:
(3) ![]()
An absolute value may be needed in one of the cosine terms if the parent triangle is obtuse. However, since we’re working with the squares for now, there’s no need for an absolute value. We have from (3) that
![]()
(Or ![]() .) Assuming
.) Assuming ![]() , we then have:
, we then have:
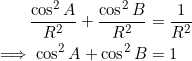
Thus, either the triangle is right-angled at ![]() , or it’s an obtuse triangle that shares several properties in common with a right-triangle.
, or it’s an obtuse triangle that shares several properties in common with a right-triangle.
Pertinent consideration
We emphasize that the equation ![]() also holds in a certain non-right triangle setting. More on this later.
also holds in a certain non-right triangle setting. More on this later.
We’re to show that ![]() , where
, where ![]() is the circumradius,
is the circumradius, ![]() is the diameter of the circumcircle of
is the diameter of the circumcircle of ![]() , and
, and ![]() is the diameter of the circumcircle of
is the diameter of the circumcircle of ![]() .
.
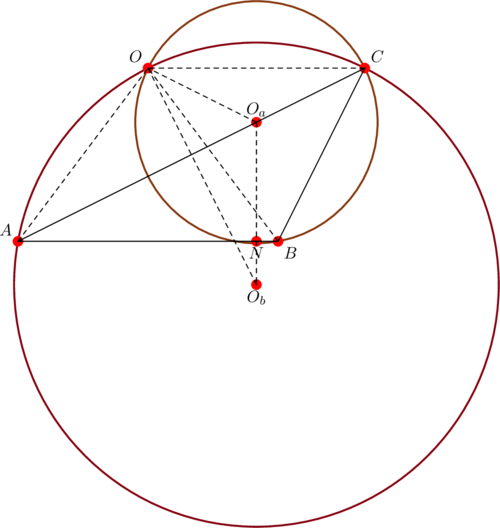
By calculation, the circumcenter ![]() is
is ![]() . Thus the circumcenter
. Thus the circumcenter ![]() of
of ![]() is
is ![]() , while the circumcenter
, while the circumcenter ![]() of
of ![]() is
is ![]() . Notice that the nine-point center
. Notice that the nine-point center ![]() shown in the diagram is co-linear with
shown in the diagram is co-linear with ![]() and
and ![]() , just like in a right triangle. Furthermore:
, just like in a right triangle. Furthermore:
So:
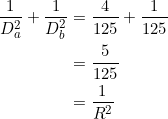
Takeaway
Suppose that triangle ![]() has side-lengths
has side-lengths ![]() , circumcenter
, circumcenter ![]() , circumradius
, circumradius ![]() , and
, and ![]() the radii of the circumcircles of
the radii of the circumcircles of ![]() and
and ![]() . Then the following statements are equivalent:
. Then the following statements are equivalent:
 is right-angled at
is right-angled at 
 .
.
Tasks
- (Geometric means) Suppose that the side-lengths of
 satisfy
satisfy  . Using the notation in this post, PROVE that:
. Using the notation in this post, PROVE that:
- (Geometric means) Suppose that the side-lengths of
 satisfy
satisfy  . Using the notation in this post, PROVE that:
. Using the notation in this post, PROVE that:
- (Growing membership) In a non-right triangle
 , let
, let  be the side-lengths,
be the side-lengths,  the altitudes,
the altitudes,  the feet of the altitudes from the respective vertices,
the feet of the altitudes from the respective vertices,  the midpoints of sides
the midpoints of sides  in that order,
in that order,  the Euler points,
the Euler points,  the circumradius,
the circumradius,  the circumcenter,
the circumcenter,  the nine-point center,
the nine-point center,  the orthocenter,
the orthocenter,  the reflection of
the reflection of  over side
over side  ,
,  the reflection of
the reflection of  over side
over side  ,
,  the reflection of
the reflection of  over side
over side  ,
,  the symmedian point,
the symmedian point,  the foot of the symmedian from vertex
the foot of the symmedian from vertex  , and
, and  the radius of the polar circle. PROVE that the following eighty-five statements are equivalent:
the radius of the polar circle. PROVE that the following eighty-five statements are equivalent:






















































 or
or 
 and
and  divide
divide  harmonically
harmonically is the reflection of
is the reflection of  over side
over side 
 is the reflection of
is the reflection of  over side
over side 
 is congruent to
is congruent to 
 is congruent to
is congruent to 
 is isosceles with
is isosceles with 
 is isosceles with
is isosceles with 
 is right angled at
is right angled at 
 is the circumcenter of
is the circumcenter of 
 is right-angled at
is right-angled at 
 is right-angled at
is right-angled at 
- quadrilateral
 is a rectangle
is a rectangle - the points
 are concyclic with
are concyclic with  as diameter
as diameter - the reflection
 of
of  over
over  lies internally on
lies internally on 
- the reflection
 of
of  over
over  lies externally on
lies externally on 
- radius
 is parallel to side
is parallel to side 
 is the reflection of
is the reflection of  over side
over side 
- segment
 is perpendicular to side
is perpendicular to side 
- the nine-point center lies on

- the orthic triangle is isosceles with

- the geometric mean theorem holds
- the bisector of
 has length
has length  , where
, where 
- the orthocenter is a reflection of vertex
 over side
over side 
- segment
 is tangent to the circumcircle at point
is tangent to the circumcircle at point 
- median
 has the same length as the segment
has the same length as the segment 
- the bisector
 of
of  is tangent to the nine-point circle at
is tangent to the nine-point circle at 
 is a convex kite with diagonals
is a convex kite with diagonals  and
and 
- altitude
 is tangent to the nine-point circle at
is tangent to the nine-point circle at 
- chord
 is a diameter of the nine-point circle
is a diameter of the nine-point circle - segment
 is tangent to the nine-point circle at
is tangent to the nine-point circle at  .
.
(More statements reserved for later. We aim to stop at statements, if possible.)
statements, if possible.)