Characterizing right triangles – High School Geometry

Take an altitude of a triangle and a median from the same vertex. Then compute their product. If the product equals the area of the triangle, then the triangle must be a right triangle.

The above property is exclusive to right triangles, and there are many other characterizations of right triangles, as seen in this list.

Today’s post will push at least two more entries into the list, in addition to that of July 14 $\cdots$ .

PROVE that the area of a right triangle is equal to the product of the altitude and median from the $90^{\circ}$

vertex.

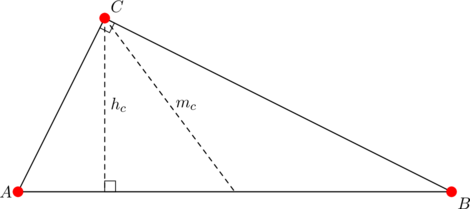
Consider a right triangle $ABC$ in which $\angle C=90^{\circ}$ as shown below:

The length of the median to the hypotenuse is half the length of the hypotenuse: $m_c=\frac{1}{2}c$ . Thus, the area is:

$\frac{AB\times h_c}{2}=\frac{c\times h_c}{2}=\frac{c}{2}h_c=m_ch_c$

If the area of a triangle is equal to the product of the altitude and median from the same vertex, PROVE that the triangle must contain a $90^{\circ}$

angle.

Suppose that the area of $\triangle ABC$ is equal to the product of the altitude $h_c$ and median $m_c$ from the same vertex $C$ . Let $a,b,c$ be the side-lengths and let $R$ be the circumradius. Then

$h_c=\frac{ab}{2R},m_c=\frac{\sqrt{2a^2+2b^2-c^2}}{2}$

The area can be given as $\frac{ab\sin C}{2}$ , and $R$ itself can be written as $R=\frac{c}{2\sin C}$ , by the extended law of sines. So:

$\begin{equation*} \begin{split} \frac{ab\sin C}{2}&=\frac{ab}{2R}\times \frac{\sqrt{2a^2+2b^2-c^2}}{2}\\ \frac{abc}{4R}&=\frac{ab\sqrt{2a^2+2b^2-c^2}}{4R}\\ c&=\sqrt{2a^2+2b^2-c^2}\\ c^2&=2a^2+2b^2-c^2\\ 2c^2&=2a^2+2b^2\\ \therefore c^2&=a^2+b^2 \end{split} \end{equation*}$

If the circle with diameter OH coincides with the nine-point circle of a triangle, PROVE that the triangle is a right triangle. As usual, $O$

and $H$

are the circumcenter and orthocenter, respectively.

Let $R$ be the circumradius of the parent triangle $ABC$ . If the circle with diameter $OH$ coincides with the nine-point circle, then we must have $OH=R$ , since the radius of the nine-point circle is $\frac{R}{2}$ .

$\therefore 9R^2-a^2-b^2-c^2=R^2\implies a^2+b^2+c^2=8R^2,$

the latter equation is one of the characterizations of right triangles given here.

In the next example we have a weaker requirement — we just ask that the nine-point circle pass through $O$ or $H$ .

If the nine-point circle passes through the circumcenter of a triangle, PROVE that the triangle is a right triangle.

Suppose that the nine-point circle passes through $O$ . Let $N$ be the nine-point center. Then $NO$ is a radius of the nine-point circle, namely $\frac{R}{2}$ . But then $NO=\frac{OH}{2}$ .

$\begin{equation*} \begin{split} \frac{R}{2}&=\frac{\sqrt{9R^2-a^2-b^2-c^2}}{2}\\ \therefore 8R^2&=a^2+b^2+c^2 \end{split} \end{equation*}$

Similarly, if the nine-point circle of a triangle passes through the orthocenter of the triangle, then the parent triangle must be a right triangle.

In $\triangle ABC$

, suppose that the square of the length of the bisector
of $\angle C$

is half the square of the harmonic mean of $a$

and $b$

. PROVE that $\angle C=90^{\circ}$

The harmonic mean of $a$ and $b$ is $\frac{2ab}{a+b}$ . The square of the length of the bisector of $\angle C$ is given by $l^2=\left(1-\left(\frac{c}{a+b}\right)^2\right)$ . We get

$\left(1-\left(\frac{c}{a+b}\right)^2\right)=\frac{1}{2}\left(\frac{2ab}{a+b}\right)^2$

and then finally $c^2=a^2+b^2$ after simplifications.

Takeaway

In $\triangle ABC$ , let $a,b,c$ be the side-lengths, $m_c$ the median from vertex $C$ , $h_c$ the altitude from vertex $C$ , $H$ the orthocenter, and $O$ the circumcenter. Then the following statements are equivalent:

the area of $\triangle ABC$ equals $m_ch_c$
$\triangle ABC$ is a right triangle with $\angle C=90^{\circ}$
the nine-point circle of $\triangle ABC$ passes through $O$
the nine-point circle of $\triangle ABC$ passes through $H$
the circle with diameter $OH$ coincides with the nine-point circle of $\triangle ABC$
$m_c$ is the geometric mean of the two equal segments it creates on the opposite side $AB$
the square of the length of the bisector of angle $C$ is half the square of the harmonic mean of $a$ and $b$ .

In the case of statement 6, one can replace the geometric mean with arithmetic mean or harmonic mean. Why?

Task

(Early fifties) In a non-right triangle , let be the side-lengths, the altitudes, the feet of the altitudes from the respective vertices, the circumradius, the circumcenter, the nine-point center, the orthocenter, the midpoint of side , and the reflection of over side . PROVE that the following fifty-four statements are equivalent:
1. $AH=b$
2. $BH=a$
3. $CH=2h_C$
4. $h_A=AF_B$
5. $h_B=BF_A$
6. $AF_C=\frac{b^2}{2R}$
7. $BF_C=\frac{a^2}{2R}$
8. $\frac{a}{c} =\frac{h_C}{AF_B}$
9. $\frac{b}{c}=\frac{h_C}{BF_A}$
10. $\frac{a}{b}=\frac{BF_A}{AF_B}$
11. $R=\frac{|a^2-b^2|}{2c}$
12. $h_C=R\cos C$
13. $\cos A=\frac{b(b^2-a^2)}{c(a^2+b^2)}$
14. $\cos B=\frac{a(a^2-b^2)}{c(a^2+b^2)}$
15. $\cos C=\frac{2ab}{a^2+b^2}$
16. $\cos^2 A+\cos^2 B=1$
17. $\sin^2 A+\sin^2 B=1$
18. $a\cos A+b\cos B=0$
19. $\sin A+\cos B=0$
20. $\cos A-\sin B=0$
21. $2\cos A\cos B+\cos C=0$
22. $a\cos A-b\cos B=\sqrt{a^2+b^2}\cos C$
23. $OH^2=5R^2-c^2$
24. $h_A^2+h_B^2=AB^2$
25. $\frac{h_A}{a}+\frac{h_B}{b}=\frac{c}{h_C}$
26. $a^2+b^2=4R^2$
27. $A-B=\pm 90^{\circ}$
28. $(a^2-b^2)^2=(ac)^2+(cb)^2$
29. $AH^2+BH^2+CH^2=8R^2-c^2$
30. $a=2R\sin A,~b=2R\cos A,~c=2R\cos 2A$
31. $\triangle ABH$ is congruent to $\triangle ABC$
32. $\triangle CNO$ is isosceles with $CN=NO$
33. $\triangle CNH$ is isosceles with $CN=NH$
34. $\triangle CHO$ is right angled at $C$
35. $N$ is the circumcenter of $\triangle CHO$
36. $\triangle O'OC$ is right-angled at $O$
37. $\triangle O'HC$ is right-angled at $H$
38. quadrilateral $O'OHC$ is a rectangle
39. the points $O',O,C,H$ are concyclic with $OH$ as diameter
40. the reflection of $O$ over $AC$ lies internally on $AB$
41. the reflection of $O$ over $BC$ lies externally on $AB$
42. radius $OC$ is parallel to side $AB$
43. $F_A$ is the reflection of $F_B$ over side $AB$
44. the nine-point center lies on $AB$
45. the orthic triangle is isosceles with $F_AF_C=F_BF_C$
46. the geometric mean theorem holds
47. the bisector of $\angle C$ has length $l$ , where $l^2=\frac{2a^2b^2}{a^2+b^2}$
48. the orthocenter is a reflection of vertex $C$ over side $AB$
49. segment $HC$ is tangent to the circumcircle at point $C$
50. median $CM$ has the same length as the segment $HM$
51. the bisector $MO$ of $AB$ is tangent to the nine-point circle at $M$
52. $AF_ABF_B$ is a convex kite with diagonals $AB$ and $F_AF_B$
53. altitude $CF_C$ is tangent to the nine-point circle at $F_C$
54. segment $HF_C$ is tangent to the nine-point circle at $F_C$ .
  ( $21$ short of the target.)
(Extra feature) If $\triangle ABC$ satisfies equation (??), PROVE that its nine-point center $N$ divides $AB$ in the ratio $|3b^2-a^2|:|b^2-3a^2|$ .