Last time we saw that the circle with diameter ![]() passes through vertex
passes through vertex ![]() if and only if the equation below holds:
if and only if the equation below holds:
(1) ![]()
Let this circle also pass through vertex ![]() . Then the nine-point center has to be
. Then the nine-point center has to be ![]() .
.
Updated equivalence
We now add the following four equivalent statements to what we had at the end of our post on August 14:
- a circle with diameter
 passes through
passes through  and
and 
- the nine-point center coincides with vertex

- the reflection of
 over
over  is
is 
- the reflection of
 over
over  is
is 
Only triangle ![]() having
having ![]() satisfies these.
satisfies these.
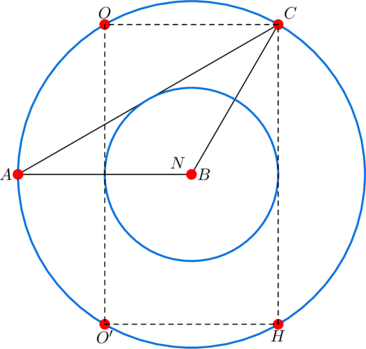
Since this circle passes through vertex ![]() , our previous post shows that equation (1) is satisfied:
, our previous post shows that equation (1) is satisfied:
![]()
Further, with ![]() as diameter, the two triangles
as diameter, the two triangles ![]() and
and ![]() are right triangles with
are right triangles with ![]() and
and ![]() .
.
By a result in this post, we conclude that the nine-point center is ![]() .
.
Easy.
Easy.
Easy.
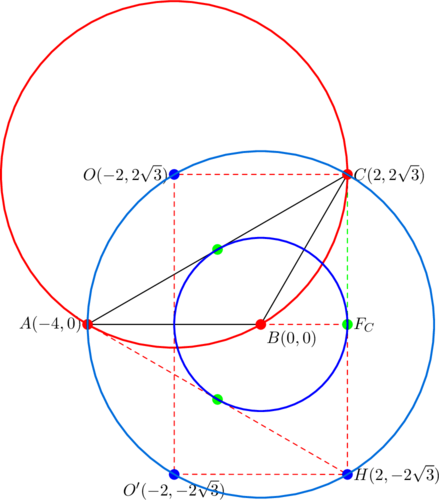
Usual example
The diagram below shows the circumcircle, the nine-point circle, and the circle with diameter ![]() .
.
Or this one:

Takeaway
Consider ![]() with side-lengths
with side-lengths ![]() , circumradius
, circumradius ![]() , circumcenter
, circumcenter ![]() , orthocenter
, orthocenter ![]() , and nine-point center
, and nine-point center ![]() . If equation (1) is satisfied, then the following statements are equivalent:
. If equation (1) is satisfied, then the following statements are equivalent:
- a circle with diameter
 passes through
passes through  and
and 
 and
and  are both equilateral
are both equilateral is tangent to the circumcircle at
is tangent to the circumcircle at 
- the orthic triangle is equilateral
- the reflection of
 over
over  is
is 
- the reflection of
 over
over  is
is 
 is equilateral
is equilateral coincides with
coincides with 


These are some of the many equivalent descriptions of the isosceles triangle ![]() in which
in which ![]() .
.
Task
- (Early fifties) In a non-right triangle
 , let
, let  be the side-lengths,
be the side-lengths,  the altitudes,
the altitudes,  the feet of the altitudes from the respective vertices,
the feet of the altitudes from the respective vertices,  the circumradius,
the circumradius,  the circumcenter,
the circumcenter,  the nine-point center,
the nine-point center,  the orthocenter,
the orthocenter,  the midpoint of side
the midpoint of side  , and
, and  the reflection of
the reflection of  over side
over side  . PROVE that the following fifty-two statements are equivalent:
. PROVE that the following fifty-two statements are equivalent:




























 is congruent to
is congruent to 
 is isosceles with
is isosceles with 
 is isosceles with
is isosceles with 
 is right angled at
is right angled at 
 is the circumcenter of
is the circumcenter of 
 is right-angled at
is right-angled at 
 is right-angled at
is right-angled at 
- quadrilateral
 is a rectangle
is a rectangle - the points
 are concyclic with
are concyclic with  as diameter
as diameter - the reflection of
 over
over  lies internally on
lies internally on 
- the reflection of
 over
over  lies externally on
lies externally on 
- radius
 is parallel to side
is parallel to side 
 is the reflection of
is the reflection of  over side
over side 
- the nine-point center lies on

- the orthic triangle is isosceles with

- the geometric mean theorem holds
- the bisector of
 has length
has length  , where
, where 
- the orthocenter is a reflection of vertex
 over side
over side 
- segment
 is tangent to the circumcircle at point
is tangent to the circumcircle at point 
- median
 has the same length as the segment
has the same length as the segment 
- the bisector
 of
of  is tangent to the nine-point circle at
is tangent to the nine-point circle at 
 is a convex kite with diagonals
is a convex kite with diagonals  and
and 
- altitude
 is tangent to the nine-point circle at
is tangent to the nine-point circle at 
- segment
 is tangent to the nine-point circle at
is tangent to the nine-point circle at  .
.
( short of the target.)
short of the target.)
- (Extra feature) If
 satisfies equation (??), PROVE that its nine-point center
satisfies equation (??), PROVE that its nine-point center  divides
divides  in the ratio
in the ratio  .
.