True.
Today’s post will specify the obtuse isosceles triangle in question. In fact, it turns out to be just a special case of triangles that satisfy our modified Pythagorean identity:
(1) ![]()
Take ![]() in equation (1) and that’s it. That’s what we seek.
in equation (1) and that’s it. That’s what we seek.
Observe that ![]() and
and ![]() . Further, equation (1) is satisfied:
. Further, equation (1) is satisfied:
![]()
and so the triangle enjoys one (and all) of the equivalent statements in our previous post. In particular, its orthocenter ![]() is a reflection of vertex
is a reflection of vertex ![]() over side
over side ![]() , namely
, namely ![]() , as shown below:
, as shown below:
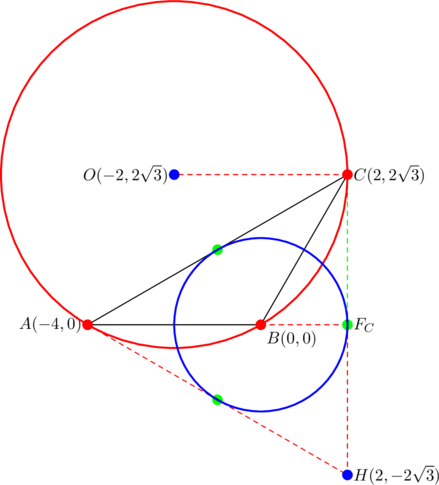
Also, the radius through vertex ![]() must be parallel to side
must be parallel to side ![]() , giving the point
, giving the point ![]() as the circumcenter. Notice how we obtained both the orthocenter
as the circumcenter. Notice how we obtained both the orthocenter ![]() and the circumcenter
and the circumcenter ![]() without a single calculation of altitude or right bisector.
without a single calculation of altitude or right bisector.
The nine-point center is the midpoint of ![]() and
and ![]() , and this is
, and this is ![]() .
.
![]() for
for ![]() oom.
oom.
Easy theorem
There’s only one triangle whose orthocenter coincides with a vertex. In our next two examples, we also show that there’s only one triangle whose nine-point center coincides with a vertex. Fair enough.
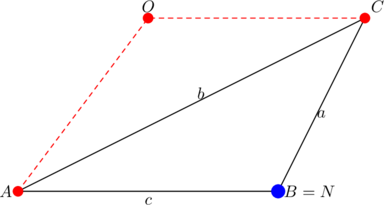
Let ![]() . Since the nine-point circle goes through the midpoint of
. Since the nine-point circle goes through the midpoint of ![]() and has radius equal to half the circumradius of the parent triangle, we have that
and has radius equal to half the circumradius of the parent triangle, we have that
![]()
But then ![]() , by the extended law of sines. So
, by the extended law of sines. So
![]()
Similarly, the nine-point circle passes through the midpoint of ![]() , so the radius from
, so the radius from ![]() to this midpoint is
to this midpoint is ![]() :
:
![]()
The only permissible choice of ![]() and
and ![]() is
is ![]() . Then
. Then ![]() .
.
![]() for
for ![]() ig.
ig.
Consider the distance from ![]() to
to ![]() , given by
, given by
![]()
Noting that ![]() and
and ![]() then yields
then yields ![]() .
.
Thus, there’s only one triangle with the property that its nine-point center coincides with one of the triangle’s vertices. And it’s the isosceles triangle with base angles of ![]() .
.
Having seen the main point, you can jump straight to the exercises at this point.
Equilateral triangles
Although the parent triangle in the preceding examples is not equilateral, there are a couple of equilateral triangles associated with it.
By example 2 we have:
![]()
when the nine-point center coincides with ![]() . Since
. Since ![]() is o
is o![]() tuse, the interior angles of the resulting orthic triangle are:
tuse, the interior angles of the resulting orthic triangle are:
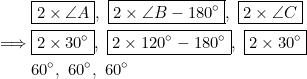
and so the orthic triangle is equilateral.
Being the circumcenter, ![]() is equidistant from
is equidistant from ![]() and
and ![]() :
: ![]() . In addition,
. In addition, ![]() . This shows that
. This shows that ![]() is equilateral. Similarly,
is equilateral. Similarly, ![]() is equilateral.
is equilateral.
By the usual notation, we have ![]() . By one of the conditions in our previous post, we have
. By one of the conditions in our previous post, we have ![]() . By example 2,
. By example 2, ![]() . Then:
. Then:
![]()
Assume that ![]() is equilateral. Since
is equilateral. Since ![]() , we have that
, we have that ![]() and
and ![]() as well.
as well.
![]()
Using ![]() in equation (1) gives
in equation (1) gives ![]() . Alternatively, we get
. Alternatively, we get ![]() and
and ![]() . Thus, by example 3, the nine-point center coincides with vertex
. Thus, by example 3, the nine-point center coincides with vertex ![]() .
.
Extra tangents
The circumcircle of any triangle that satisfies equation (1) comes naturally with one tangent: the segment from the orthocenter ![]() is a tangent to the circumcircle at vertex
is a tangent to the circumcircle at vertex ![]() . In the event that the nine-point center coincides with vertex
. In the event that the nine-point center coincides with vertex ![]() , we get two extra tangents.
, we get two extra tangents.
Look here:
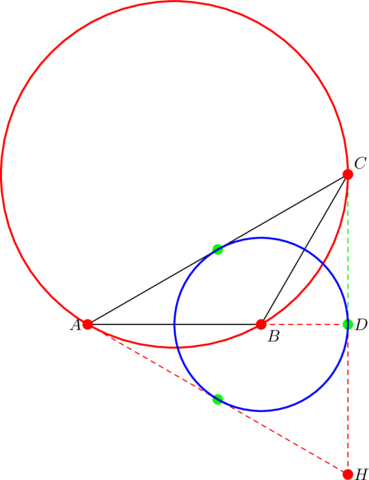
Look here:

Look here:

Takeaway
Consider ![]() with side-lengths
with side-lengths ![]() , circumradius
, circumradius ![]() , circumcenter
, circumcenter ![]() , orthocenter
, orthocenter ![]() , and nine-point center
, and nine-point center ![]() . If equation (1) is satisfied, then the following statements are equivalent:
. If equation (1) is satisfied, then the following statements are equivalent:
 and
and  are both equilateral
are both equilateral is tangent to the circumcircle at
is tangent to the circumcircle at 
- the orthic triangle is equilateral
 is equilateral
is equilateral coincides with
coincides with 


A triangle that satisfies these has to have ![]() .
.
Tasks
- Let
 be the orthocenter, circumcenter, and nine-point center of
be the orthocenter, circumcenter, and nine-point center of  . If
. If  , PROVE that:
, PROVE that:
- the points
 are concyclic
are concyclic - the circumcenter of
 is
is 
- the circumcenter of
 is
is 
- the incenter of
 is
is 
- the nine-point circle of
 coincides with the incircle of
coincides with the incircle of  .
.
- the points
- In
 , let
, let  be the circumcenter and
be the circumcenter and  the circumradius. Let
the circumradius. Let  be the circumcenter of
be the circumcenter of  and let
and let  be its circumradius. If equation (1) is satisfied, PROVE that:
be its circumradius. If equation (1) is satisfied, PROVE that:

 , where
, where  is the altitude from
is the altitude from  and
and  is the diameter of the circumcircle of
is the diameter of the circumcircle of  .
.
- (Expanded list) Consider a non-right triangle
 with side-lengths
with side-lengths  , altitudes
, altitudes  , circumradius
, circumradius  , circumcenter
, circumcenter  , nine-point center
, nine-point center  , and orthocenter
, and orthocenter  . PROVE that the following twenty eight statements are equivalent:
. PROVE that the following twenty eight statements are equivalent:




















- radius
 is parallel to side
is parallel to side 
- the nine-point center lies on

- the geometric mean theorem holds
- the orthic triangle is obtuse isosceles
- the bisector of
 has length
has length  , where
, where 
- the orthocenter is a reflection of vertex
 over side
over side 
- segment
 is tangent to the circumcircle at point
is tangent to the circumcircle at point 
- segment
 is tangent to the nine-point circle at
is tangent to the nine-point circle at  , where
, where  is the foot of the altitude from vertex
is the foot of the altitude from vertex  .
.
(We’ll continue to update this list until we reach at least a certain limit).
- (Euler line) Consider a right triangle
 with circumcenter
with circumcenter  , nine-point center
, nine-point center  , and
, and  . Let
. Let  be the circumcenter of
be the circumcenter of  and let
and let  be the circumcenter of
be the circumcenter of  . Then the points
. Then the points  are co-linear, as we saw earlier and will see later. PROVE that:
are co-linear, as we saw earlier and will see later. PROVE that:
 is similar to
is similar to 
 divides
divides  in the ratio
in the ratio  (or
(or  )
)- the line segment
 is perpendicular to the Euler line
is perpendicular to the Euler line - the quadrilateral
 is a kite (don’t confuse
is a kite (don’t confuse  with a certain functional group in organic chemistry).
with a certain functional group in organic chemistry).
- (Euler line) If triangle
 satisfies equation (1), PROVE that:
satisfies equation (1), PROVE that:
 is perpendicular to the Euler line
is perpendicular to the Euler line is similar to the parent
is similar to the parent 
 is similar to the orthic triangle of
is similar to the orthic triangle of 
 divides
divides  in the ratio
in the ratio  (or
(or  ).
).