Earlier, we considered the “altitude version” of the the geometric mean theorem, which states that
(1) ![]()
as per the diagram above. There is also the “leg version” of the geometric mean theorem:
(2) ![]()
where ![]() is the hypotenuse.
is the hypotenuse.
If ![]() denotes the circumradius, then
denotes the circumradius, then ![]() in a right triangle and so the relations in (2) can be re-written:
in a right triangle and so the relations in (2) can be re-written:
(3) ![]()
Since ![]() and
and ![]() are merely the distances from the foot of the altitude, nothing makes equation (3) exclusive to right triangles. As such, we’ll now derive similar relations for non-right triangles that satisfy our modified Pythagorean identity
are merely the distances from the foot of the altitude, nothing makes equation (3) exclusive to right triangles. As such, we’ll now derive similar relations for non-right triangles that satisfy our modified Pythagorean identity
(4) ![]()

(5) ![]()
(6) ![]()
You may jump straight to the exercises after the sixth example.

Apply Pythagorean theorem to ![]() and remember that equation (4) is equivalent to
and remember that equation (4) is equivalent to ![]() . This gives:
. This gives:
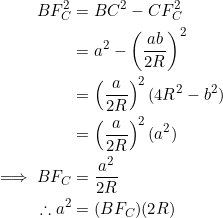
Co-linearity

As before apply Pythagorean theorem to ![]() , bearing in mind that equation (4) is equivalent to
, bearing in mind that equation (4) is equivalent to ![]() . This gives:
. This gives:
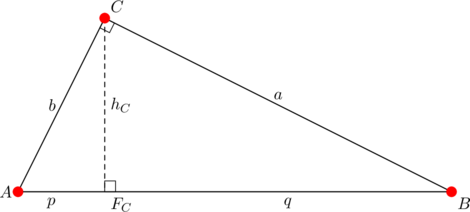
As per the diagram below

we normally have
![Rendered by QuickLaTeX.com \[BF_C=\sqrt{a^2-\left(\frac{ab}{2R}\right)^2}=\frac{a}{2R}\sqrt{4R^2-b^2}.\]](https://blog.fridaymath.com/wp-content/ql-cache/quicklatex.com-0228635022fd196305cd32dcf91cc5a3_l3.png)
If in addition ![]() , then:
, then:
![]()
which we know to be equivalent to equation (4).
Coincidence
As per the diagram below

we normally have
![Rendered by QuickLaTeX.com \[AF_C=\sqrt{b^2-\left(\frac{ab}{2R}\right)^2}=\frac{b}{2R}\sqrt{4R^2-a^2}.\]](https://blog.fridaymath.com/wp-content/ql-cache/quicklatex.com-25cbdc5e6f23428ac5f01c1d2ff42bac_l3.png)
If in addition ![]() , then:
, then:
![]()
which we know to be equivalent to equation (4).
- we feel that the usual ten examples appear too much to digest at once, especially because we really want the reader to get the best out of every post;
- we will be returning to in-class teaching, after having taken full advantage of teaching from home — and saving some time — for the past few months.
Assuming the reader actually puts mind to the things we write, probably reducing the volume will aid better understanding of the material. We may end up reducing the “volume” and increasing the “pressure”, to obey Boyle’s law.
From the diagram below

we get ![]() . Notice that equation (4) holds:
. Notice that equation (4) holds:
![]()
and so we can compute the circumradius ![]() using
using ![]() , an equation that’s equivalent to (4).
, an equation that’s equivalent to (4).
![]()
Also, ![]() . Then:
. Then:
![]()
Here, the only modification to the previous example is that ![]() this time around. Then:
this time around. Then:
![]()
From the diagram below
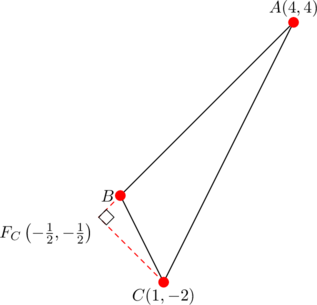
we get ![]() . Notice that equation (4) holds:
. Notice that equation (4) holds:
![]()
and so we can compute the circumradius ![]() using
using ![]() , an equation that’s equivalent to (4).
, an equation that’s equivalent to (4).
![]()
Also, ![]() and
and ![]() . Then:
. Then:
![Rendered by QuickLaTeX.com \[a^2=5~\&~(BF_C)(2R)=\left(\frac{1}{2}\sqrt{2}\right)\left(2\times \frac{5\sqrt{2}}{2}\right)=5\]](https://blog.fridaymath.com/wp-content/ql-cache/quicklatex.com-18f239936d388767a68f6614cbcfa520_l3.png)
Circumradii
Recall from the previous example that the foot of the altitude from ![]() is
is ![]() . The only modification is the calculation of
. The only modification is the calculation of ![]() , and it is
, and it is
![Rendered by QuickLaTeX.com \[AF_C=\sqrt{\left(4+\frac{1}{2}\right)^2+\left(4+\frac{1}{2}\right)^2}=\frac{9}{2}\sqrt{2}.\]](https://blog.fridaymath.com/wp-content/ql-cache/quicklatex.com-a6cb35082adc4e8c64768dec88c5625e_l3.png)
Then
![Rendered by QuickLaTeX.com \[b^2=45~\&~(AF_C)(2R)=\left(\frac{9}{2}\sqrt{2}\right)\left(2\times\frac{5\sqrt{2}}{2}\right)=45\]](https://blog.fridaymath.com/wp-content/ql-cache/quicklatex.com-746a3daa91d087b03f1a165a81d2d974_l3.png)
From the diagram below
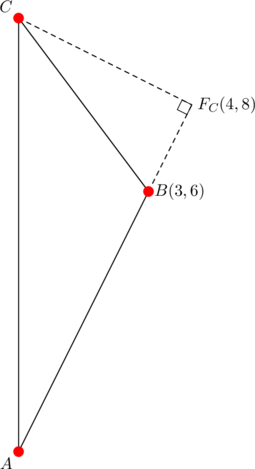
we get ![]() . Notice that equation (4) holds:
. Notice that equation (4) holds:
![]()
and so we can compute the circumradius ![]() using
using ![]() , an equation that’s equivalent to (4).
, an equation that’s equivalent to (4).
![]()
Also, ![]() , being the distance from
, being the distance from ![]() to
to ![]() . Then:
. Then:
![Rendered by QuickLaTeX.com \[a^2=25~\&~(BF_C)(2R)=(\sqrt{5})\left(2\times \frac{5\sqrt{5}}{2}\right)=25\]](https://blog.fridaymath.com/wp-content/ql-cache/quicklatex.com-79dcb63c3c6f722b8e59bb7d92013ca9_l3.png)
As in the preceding example, the foot of the altitude from vertex ![]() is
is ![]() . The distance
. The distance ![]() is then
is then ![]() . The circumradius is as before:
. The circumradius is as before: ![]() . Then:
. Then:
![Rendered by QuickLaTeX.com \[b^2=45~\&~(AF_C)(2R)=(4\sqrt{5})\left(2\times\frac{5\sqrt{5}}{2}\right)=45.\]](https://blog.fridaymath.com/wp-content/ql-cache/quicklatex.com-85ffd55a6b48275feea77bb9c0141855_l3.png)
Takeaway
In a non-right ![]() , let
, let ![]() be the side-lengths,
be the side-lengths, ![]() the circumradius, and
the circumradius, and ![]() the foot of the altitude from vertex
the foot of the altitude from vertex ![]() . Then the following statements are equivalent:
. Then the following statements are equivalent:
 satisfy equation (4)
satisfy equation (4)

 .
.
And many more.
Task
- (Late thirties) In a non-right triangle
 , let
, let  be the side-lengths,
be the side-lengths,  the altitudes,
the altitudes,  the feet of the altitudes from the respective vertices,
the feet of the altitudes from the respective vertices,  the circumradius,
the circumradius,  the circumcenter,
the circumcenter,  the nine-point center, and
the nine-point center, and  the orthocenter. PROVE that the following thirty seven statements are equivalent:
the orthocenter. PROVE that the following thirty seven statements are equivalent:




























- radius
 is parallel to side
is parallel to side 
- the nine-point center lies on

- the orthic triangle is obtuse isosceles
- the geometric mean theorem holds
- the bisector of
 has length
has length  , where
, where 
- the orthocenter is a reflection of vertex
 over side
over side 
- segment
 is tangent to the circumcircle at point
is tangent to the circumcircle at point 
 is a convex kite with diagonals
is a convex kite with diagonals  and
and 
- segment
 is tangent to the nine-point circle at
is tangent to the nine-point circle at  .
.
(In terms of sheer numbers, the conditions above have now surpassed the number of statements in the Invertible Matrix Theorem. Next stop is to top the number of statements characterizing tangential quadrilaterals. Next stop after that? To stop pestering you with the same exercises over and over.)
- (Less tasks)