
If a non-right triangle, like the one shown above, satisfies the identity
(1) ![]()
then we can recast equation (1) in a form that looks more like the usual Pythagorean identity, namely:
(2) ![]()
As ![]() , we have an approximate Pythagorean identity
, we have an approximate Pythagorean identity
(3) ![]()
Consider the following diagram:

Let ![]() be the circumradius and suppose that
be the circumradius and suppose that ![]() (if
(if ![]() , take
, take ![]() ). We’ll use some properties that are consequences of equation (1), including the one from our previous post:
). We’ll use some properties that are consequences of equation (1), including the one from our previous post:
![]()
Then:
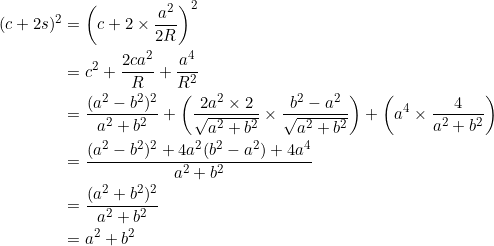
From the diagram below
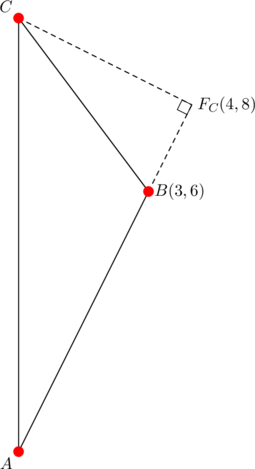
we get ![]() . Equation (1) holds:
. Equation (1) holds:
![]()
as well as equation (2), because:
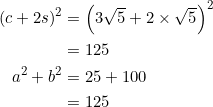
Note that ![]() and
and ![]() can switch places. From the diagram below
can switch places. From the diagram below

we get ![]() . Equation (1) holds:
. Equation (1) holds:
![]()
as well as equation (2), because:
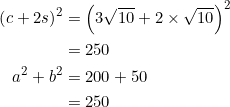
From the diagram below

we get ![]() . Notice that equation (1) holds:
. Notice that equation (1) holds:
![]()
as well as equation (2), since:
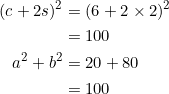
From the diagram below
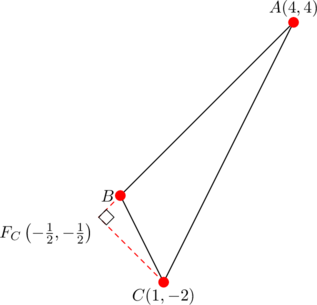
we get ![]() . Equation (1) holds:
. Equation (1) holds:
![]()
as well as equation (2), since
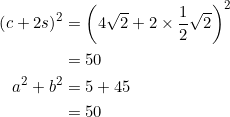
As in this post, notice that the title of today’s post can be abbreviated as API, an absolutely endearing term in computer programming.
Takeaway
In a non-right ![]() , let
, let ![]() be the side-lengths,
be the side-lengths, ![]() the circumradius,
the circumradius, ![]() the circumcenter,
the circumcenter, ![]() the orthocenter, and
the orthocenter, and ![]() the nine-point center. Then the following statements are equivalent:
the nine-point center. Then the following statements are equivalent:


 is isosceles with
is isosceles with 
 is isosceles with
is isosceles with 
 is the circumcenter of
is the circumcenter of 
 is right angled at
is right angled at  .
.
Don’t confuse ![]() with the functional group of an aldehyde.
with the functional group of an aldehyde.
Task
- (Early fourties) In a non-right triangle
 , let
, let  be the side-lengths,
be the side-lengths,  the altitudes,
the altitudes,  the feet of the altitudes from the respective vertices,
the feet of the altitudes from the respective vertices,  the circumradius,
the circumradius,  the circumcenter,
the circumcenter,  the nine-point center, and
the nine-point center, and  the orthocenter. PROVE that the following forty four statements are equivalent:
the orthocenter. PROVE that the following forty four statements are equivalent:




























 is congruent to
is congruent to 
 is isosceles with
is isosceles with 
 is isosceles with
is isosceles with 
 is right angled at
is right angled at 
 is the circumcenter of
is the circumcenter of 
- radius
 is parallel to side
is parallel to side 
- the nine-point center lies on

- the orthic triangle is isosceles with

- the geometric mean theorem holds
- the bisector of
 has length
has length  , where
, where 
- the orthocenter is a reflection of vertex
 over side
over side 
- segment
 is tangent to the circumcircle at point
is tangent to the circumcircle at point 
- the bisector
 of
of  is tangent to the nine-point circle at
is tangent to the nine-point circle at 
 is a convex kite with diagonals
is a convex kite with diagonals  and
and 
- altitude
 is tangent to the nine-point circle at
is tangent to the nine-point circle at 
- segment
 is tangent to the nine-point circle at
is tangent to the nine-point circle at  .
.
(Wow!!! The numbers increased so rapidly, from twenty one a few days ago.)
- (Extra feature) If
 satisfies equation (1), PROVE that its nine-point center
satisfies equation (1), PROVE that its nine-point center  divides
divides  in the ratio
in the ratio  .
.