On the geometric mean theorem – High School Geometry

Given a right triangle with an altitude $h_C$

as shown below:

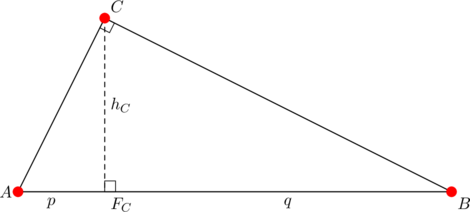
the geometric mean theorem states that

(1) $\begin{equation*} h_C=\sqrt{pq}=\sqrt{AF_C\times BF_C} \end{equation*}$

As shown here, equation (1) is equivalent to the Pythagorean identity:

(2) $\begin{equation*} c^2=a^2+b^2 \end{equation*}$

However, the equivalence holds because the altitude is internal. In the case of an external altitude, we present an analogous geometric mean theorem:

(3) $\begin{equation*}h_C=\sqrt{AF_C\times BF_C}\end{equation*}$

Here, equation (3) is equivalent to:

(4) $\begin{equation*} \begin{split} (a^2-b^2)^2&=(ac)^2+(cb)^2 \end{split} \end{equation*}$

Consider $\triangle ABC$

with vertices at $A(-6,0)$

, $B(0,0)$

, $C(2,4)$

. Let $F_C$

be the foot of the altitude from vertex $C$

, and let $h_C$

be the length of this altitude. Show that $h_C=\sqrt{AF_C\times BF_C}$

We have

$h_C=4,~AF_C=8,~BF_C=2,\boxed{4=\sqrt{2\times 8}}\implies h_C=\sqrt{AF_C\times BF_C}$

External altitudes

In examples 2 and 3 below, we prove the equivalence between equations (3) and (4).

Establish an analogous geometric mean theorem for obtuse triangles.

Apply the Pythagorean theorem to triangles $ACF_C$ and $BCF_C$ :

$\begin{equation*} \begin{split} h_C^2&=a^2-s^2\\ h_C^2&=b^2-(c+s)^2\\ \therefore a^2-s^2&=b^2-(c+s)^2\\ s&=\frac{(b^2-a^2)-c^2}{2c}\\ &=\frac{a^2}{\sqrt{a^2+b^2}}\\ AF_C&=c+s\\ &=\frac{b^2-a^2}{\sqrt{a^2+b^2}}+\frac{a^2}{\sqrt{a^2+b^2}}\\ &=\frac{b^2}{\sqrt{a^2+b^2}}\\ h_C&=\frac{ab}{\sqrt{a^2+b^2}}\\ AF_C\times BF_C&=(c+s)\times s\\ &=\frac{b^2}{\sqrt{a^2+b^2}}\times \frac{a^2}{\sqrt{a^2+b^2}}\\ \therefore h_C&=\sqrt{AF_C\times BF_C} \end{split} \end{equation*}$

Note that $\triangle ACF_C$

and $\triangle BCF_C$

are similar, so one can actually use this fact to obtain an easier proof.

PROVE that if an obtuse triangle enjoys the geometric mean theorem, then a relation of the form (4) must hold.

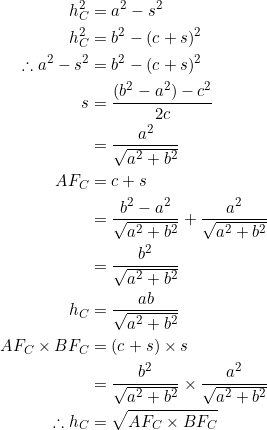
Assume that in the diagram above one has $h_C=\sqrt{AF_C\times BF_C}$ . As before, $h_C^2=a^2-s^2=b^2-(c+s)^2$ , giving

$s=\frac{b^2-a^2-c^2}{2c} \implies c+s=\frac{b^2-a^2+c^2}{2c}$

$\begin{equation*} \begin{split} h_C^2&=AF_C\times BF_C\\ \therefore a^2-\left(\frac{b^2-a^2-c^2}{2c}\right)^2&=\scriptstyle\left(\frac{b^2-a^2+c^2}{2c}\right)\left(\frac{b^2-a^2-c^2}{2c}\right)\\ 4a^2c^2-\left[(b^2-a^2)^2+c^4-2c^2(b^2-a^2)\right]&=(b^2-a^2)^2-c^4\\ \therefore c^2(a^2+b^2)&=(b^2-a^2)^2\\ \end{split} \end{equation*}$

Thus, we have a characterization of obtuse triangles that satisfy the geometric mean theorem.

Extra attributes

When a triangle satisfies equation (4), it is peculiar in its own right, but also shares some things in common with the right triangle.

If $\triangle ABC$

satisfies equation (4), PROVE that $AF_B=AF_A$

and $BF_A=BF_B$

, where $F_A,F_B$

are the feet of the altitudes from $A,B$

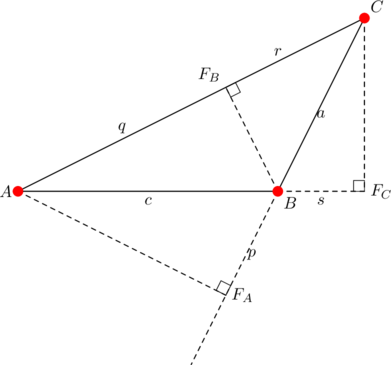
Note that (by definition) $AF_A=h_A$ and $BF_B=h_B$ , where $h_A$ and $h_B$ are the lengths of the altitudes from $A$ and $B$ . From the above diagram:

$\begin{equation*} \begin{split} AF_B^2&=AB^2-BF_B^2\\ &=c^2-h_B^2\\ &=c^2-\left(\frac{ac}{2R}\right)^2\\ &=\frac{c^2}{4R^2}(4R^2-a^2)\\ &=\frac{c^2}{4R^2}(b^2)\Longleftarrow a^2+b^2=4R^2\\ &=\left(\frac{bc}{2R}\right)^2\\ &=h_A^2\\ \therefore AF_B&=h_A=AF_A \end{split} \end{equation*}$

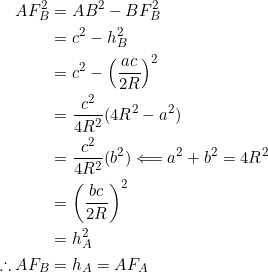
Similarly, $BF_A=BF_B$ .

Suppose that $\triangle ABC$

satisfies equation (4). Using the diagram below, PROVE that $ap=cs$

From the previous example we had $p=h_B$ and $BF_B=h_B$ , so:

$ap=ah_B=a\frac{ac}{2R} =\frac{a^2c}{2R}.$

From the diagram

$s=\sqrt{a^2-h_C^2}=\sqrt{a^2-\left(\frac{ab}{2R}\right)^2}=\frac{a^2}{2R}\implies cs=\frac{a^2c}{2R}.$

Suppose that $\triangle ABC$

satisfies equation (4). Using the diagram below, PROVE that $p(p+a)=qr$

Note that $q=h_A$ (example 4) and $r=\frac{a}{R}h_C$ , where $R$ is the circumradius.

$qr=\frac{a}{R}h_Ah_C.$

And

$p(p+a)=h_B(h_B+a)=\frac{ac}{2R}\left(\frac{ac}{2R}+a\right)=\frac{a^2c}{R}\frac{b^2}{4R^2}=\frac{a}{R}(h_Ah_C).$

(Along the line we used equation (4) and its equivalent representation $a^2+b^2=4R^2$ .)

Conclusion: $p(p+a)=qr$ or $BF_A\times CF_A=AF_B\times CF_B$ .

If $\triangle ABC$

satisfies equation (4), PROVE that $\cos^2A+\cos^2B=1$

The relation $\cos^2A+\cos^2B=1$ also holds for right triangles. Using equation (4) and the cosine formula, we obtain

$\cos A=-\frac{b}{\sqrt{a^2+b^2}},~\cos B=\frac{a}{\sqrt{a^2+b^2}}\implies \cos^2A+\cos^2B=1.$

If $\triangle ABC$

satisfies equation (4), PROVE that $A-B=90^{\circ}$

or $B-A=90^{\circ}$

This is probably the easiest way to see the relationship between right triangles and triangles satisfying equation (4).

From example 7 above we had $\cos^2A+\cos^2B=1$ . But then $\cos^2A+\sin^2A=1$ also, giving $\cos^2A+\cos^2B=\cos^2 A+\sin^2A$ .

$\cos B=\pm \sin A\implies A+B=90^{\circ}~\textrm{or}~B-A=90^{\circ}.$

Our triangle is obtuse so we choose $B-A=90^{\circ}$ .

If $\cos^2A+\cos^2B=1$

, PROVE that $\triangle ABC$

is either a right triangle or else satisfies equation (4).

Using $\cos^2A+\cos^2B=1$ , the cosine formula, and skipping a couple of steps, we have:

$\begin{equation*} \begin{split} \left(\frac{b^2+c^2-a^2}{2bc}\right)^2+\left(\frac{a^2+c^2-b^2}{2ac}\right)^2&=1\\ (a^2+b^2)c^4-2(a^4+b^4)c^2+(a^2+b^2)(a^2-b^2)&=0\\ \frac{2(a^4+b^4)\pm\sqrt{4(a^4+b^4)^2-4(a^2+b^2)^2(a^2-b^2)^2}}{2(a^2+b^2)}&=c^2\\ \frac{2(a^4+b^4)\pm 4a^2b^2}{2(a^2+b^2)}&=c^2\\ a^2+b^2&=c^2\\ \textrm{or}~\frac{(a^2-b^2)^2}{a^2+b^2}&=c^2 \end{split} \end{equation*}$

The second possibility $\frac{(a^2-b^2)^2}{a^2+b^2}=c^2$ is just equation (4) re-arranged.

Essential awareness

The preceding examples show that our newest arrival — any $\triangle ABC$ satisfying equation (4) –“rivals” the right triangle in many aspects. More on that later. For now, any triangle whose side-slopes form a geometric progression is also comparable to a right triangle. There, a modified geometric mean theorem holds (see example 10).

In $\triangle ABC$

, let the slopes of the sides $AB,BC,CA$

be $a,ar,ar^2$

. Let $h_A$

be the length of the altitude from vertex $A$

. Then

(5) $\begin{equation*}h_A=\frac{ar(r-1)}{\sqrt{|(a^2r^2+r)(a^2r^3+1)|}}\sqrt{pq}=k\sqrt{pq},~~\frac{p}{q}=\frac{a^2r^2+r}{a^2r^3+1} \end{equation*}$

where $p+q=BC$ and $k=\frac{ar(r-1)}{\sqrt{|(a^2r^2+r)(a^2r^3+1)|}}$ .

Earlier aim

Our original plan was to focus on equation (5) throughout today, but we were redirected along the way. Kindly bear with us for not completely fulfilling the promise made in example 8 of our post on December 28, 2020.

Consider triangle $ABC$

with vertices at $A(1,4)$

, $B(3,6)$

, and $C(0,0)$

. Verify that equation (5) is satisfied.

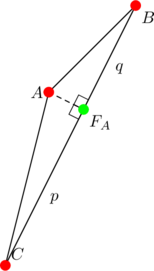
The foot of the altitude from $A$ is $F_A(9/5,18/5)$ , as shown above. By the distance formula:

$p=\frac{9}{5}\sqrt{5},~q=\frac{6}{5}\sqrt{5},~h_A=\frac{2}{5}\sqrt{5}.$

The slopes of the sides of $\triangle ABC$ form a geometric progression with $a=1$ and $r=2$ , so we can now $k$ al $k$ ulate $k$ :

$k=\frac{ar(r-1)}{\sqrt{(a^2r^2+r)(a^2r^3+1)}}=\frac{2(2-1)}{\sqrt{(4+2)(8+1)}}=\frac{\sqrt{6}}{9}$

Finally we compare both $h_A$ and $k\sqrt{pq}$ :

$h_A=\frac{2}{5}\sqrt{5},~k\sqrt{pq}=\frac{\sqrt{6}}{9}\sqrt{\frac{9}{5}\sqrt{5}\times \frac{6}{5}\sqrt{5}}=\frac{2}{5}\sqrt{5}.$

Equal. Equation (5) is satisfied.

Takeaway

For any obtuse triangle $ABC$ , the following statements are equivalent:

$(a^2-b^2)^2=(ac)^2+(cb)^2$
the orthic triangle is isosceles
the geometric mean theorem holds.

We have a longer chain of equivalence in the exercises below.

Tasks

(Long chain) For any obtuse triangle , PROVE that each of the following statements implies the others:
- $\cos A=\frac{b(b^2-a^2)}{c(a^2+b^2)}$
- $\cos B=\frac{a(a^2-b^2)}{c(a^2+b^2)}$
- $\cos C=\frac{2ab}{a^2+b^2}$
- $\cos^2 A+\cos^2 B=1$
- $\sin^2 A+\sin^2 B=1$
- $a\cos A+b\cos B=0$
- $2\cos A\cos B+\cos C=0$
- $a^2+b^2=4R^2$
- $h_C=R\cos C$
- $h_A^2+h_B^2=AB^2$
- $\frac{h_A}{a}+\frac{h_B}{b}=\frac{c}{h_C}$
- $(a^2-b^2)^2=(ac)^2+(cb)^2$
- $A-B=90^{\circ}$ or $B-A=90^{\circ}$
- the orthic triangle is isosceles
- the geometric mean theorem holds.
  (Some of the statements above are satisfied in a right triangle, but the entire chain of statements are no longer equivalent in that case.) For something different, some of the above statements are clearly redundant; notwithstanding, just admire the sheer quantity. The aim is to increase the numbers until as many statements as there are in the Invertible Matrix Theorem are reached (and “breached”).
(Linear combination) Suppose that satisfies equation (4).
- PROVE that $a\cos A-b\cos B-\sqrt{a^2+b^2}\cos C=0$ .
- Write $a\cos A-b\cos B$ in the form $k\sin(B-A)$ .
Consider with vertices at , , . Denote its orthocenter and circumcenter by and as usual.
- Verify that $a^2=45,b^2=5,c^2=32$ . Hence, deduce that $(a^2-b^2)^2=(ac)^2+(cb)^2$ (in other words, equation (4) is satisfied)
- PROVE that $O\equiv \left(\frac{7}{2},\frac{1}{2}\right)$ . Hence, deduce that radius $OC$ is parallel to side $AB$
- PROVE that $H\equiv \left(-2,1\right)$ . Deduce that the orthocenter is the reflection of vertex $C$ over side $AB$ .
PROVE that the two statements below are equivalent for a triangle :
- it is a right triangle
- its area is $h_C\times m_C$ , the product of the altitude and median from the same vertex.
Consider with side-lengths and altitudes .
- If $\angle C=90^{\circ}$ , PROVE that $\frac{a}{h_A}+\frac{b}{h_B}=\frac{c}{h_C}$ and $\frac{h_A}{a}+\frac{h_B}{b}=\frac{c}{h_C}$ .
- Deduce that $\left(\frac{c}{h_C}\right)^2-\frac{a}{b}\frac{h_B}{h_A}-\frac{b}{a}\frac{h_A}{h_B}=2$ , under the condition above.
- Suppose that the triangle satisfies equation (4) instead. PROVE that $\frac{h_A}{a}+\frac{h_B}{b}=\frac{c}{h_C}$ .
- Deduce that $\frac{h_A}{a}+\frac{h_B}{b}=\frac{h_C}{c}$ if, and only if, $\frac{b}{a}$ is the golden ratio, for any triangle satisfying equation (4).