On October 14, we promised that a slope-based derivation of the golden ratio will be aired before the end of this year; and on that premise, here we are. Actually, prior to this episode, the golden ratio has already made three cameos, but this is its full scenario.
Antisymmetric cubic
Also called anti-palindromic, due to the coefficients. Not limited to cubics though. An example is ![]() , the binomial expansion of
, the binomial expansion of ![]() . Another example is
. Another example is ![]() . And so on. You get the gist.
. And so on. You get the gist.
In any right isosceles triangle with slopes in geometric progression, PROVE that the common ratio ![]() satisfies the cubic equation
satisfies the cubic equation ![]() .
.
Let ![]() be right isosceles and let the geometric progression of slopes be
be right isosceles and let the geometric progression of slopes be ![]() for sides
for sides ![]() , respectively.
, respectively.
From this post, the slopes of the medians to these sides will be
![]()
respectively.
Now, side ![]() cannot be the hypotenuse (you know why, right?) This leaves us with either
cannot be the hypotenuse (you know why, right?) This leaves us with either ![]() or
or ![]() as the hypotenuse.
as the hypotenuse.
First suppose that ![]() is the hypotenuse. Then
is the hypotenuse. Then ![]() and so
and so
(1) ![]()
By the isosceles condition, ![]() and so the median from vertex
and so the median from vertex ![]() is perpendicular to side
is perpendicular to side ![]() . This gives:
. This gives:
(2) ![]()
Combine equations (1) and (2):
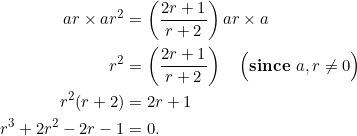
There we gold. Switching the hypotenuse won’t alter the fact that the equation holds. For suppose instead that ![]() is the hypotenuse. Then
is the hypotenuse. Then ![]() , giving
, giving
(3) ![]()
The isosceles condition forces ![]() , in which case the median from vertex
, in which case the median from vertex ![]() meets
meets ![]() at right angles:
at right angles:
(4) ![]()
As before, combining equations (3) and (4) yields ![]() .
.
In any right isosceles triangle with side-slopes in geometric progression, PROVE that the common ratio ![]() satisfies
satisfies ![]() .
.
From example 1 above, the common ratio ![]() satisfies the cubic equation
satisfies the cubic equation
![]()
which can be easily factored because of the “antisymmetric” coefficients:
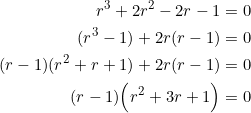
Slope considerations means we cannot have ![]() . This leaves us with the choice
. This leaves us with the choice ![]() (see here for a different proof).
(see here for a different proof).
Ancient concept
The golden ratio is a fascinating quantity, not just because it has been around since antiquity, but also because of its ubiquity. And, as shown below, it does seem to have an affinity for right isosceles triangles with slopes in geometric progressions, considering the frequency with which it turns up in their “vicinity”.
In a right isosceles triangle with slopes in geometric progression ![]() , PROVE that the the common ratio
, PROVE that the the common ratio ![]() is either
is either ![]() or
or ![]() . (In other words,
. (In other words, ![]() is either the negative of the square of the golden ratio, or the negative of the square of the reciprocal of the golden ratio.)
is either the negative of the square of the golden ratio, or the negative of the square of the reciprocal of the golden ratio.)
The golden ratio is ![]() and its reciprocal is
and its reciprocal is ![]() .
.
The common ratio ![]() of our right isosceles triangle satisfies the quadratic equation
of our right isosceles triangle satisfies the quadratic equation
![]()
Let’s split the two roots, like so:
![]()
What we want now follows immediately:
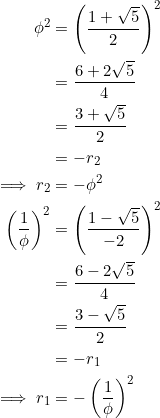
If you ever needed an example that shows that the common ratio in a right triangle (with slopes in geometric progression) is necessarily negative, this is it.
In a right isosceles triangle with slopes in geometric progression ![]() , PROVE that the the first term
, PROVE that the the first term ![]() — either the golden ratio or its negative, if the hypotenuse has slope
— either the golden ratio or its negative, if the hypotenuse has slope ![]() . Under the same conditions, PROVE also that we have
. Under the same conditions, PROVE also that we have ![]() — either the reciprocal of the golden ratio or the negative of its reciprocal.
— either the reciprocal of the golden ratio or the negative of its reciprocal.
Suppose that the hypotenuse has slope ![]() . Then the legs’ slopes are
. Then the legs’ slopes are ![]() and
and ![]() . Consequently:
. Consequently:
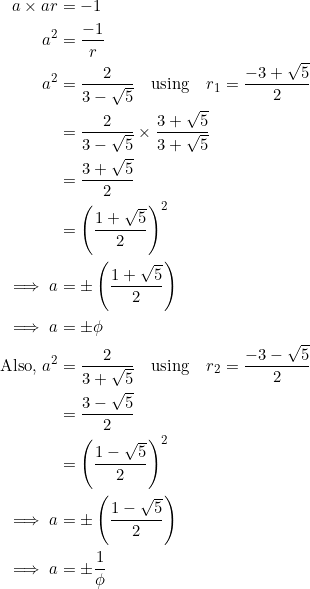
Does this example provide a golden opportunity for us to reconsider the definition of a golden triangle?
In a right isosceles triangle with slopes in geometric progression ![]() , PROVE that the the first term
, PROVE that the the first term ![]() is either
is either ![]() or
or ![]() , if the hypotenuse has slope
, if the hypotenuse has slope ![]() .
.
If the hypotenuse has slope ![]() , then the legs are
, then the legs are ![]() and
and ![]() . Consequently:
. Consequently:

Absolute character
In a right isosceles triangle with side-slopes ![]() , we always have
, we always have
(5) ![]()
when the side with slope ![]() is the hypotenuse, and we always have
is the hypotenuse, and we always have
(6) ![]()
when the hypotenuse is the side with slope ![]() . Think “antisymmetry” as being behind these equations.
. Think “antisymmetry” as being behind these equations.
Let ![]() be the slopes of the sides of a right isosceles triangle, with the hypotenuse having slope
be the slopes of the sides of a right isosceles triangle, with the hypotenuse having slope ![]() . PROVE that
. PROVE that ![]() or
or ![]() .
.
In view of example 4 above, there are four possibilities for ![]() , viz:
, viz: ![]() or
or ![]() . The “base” case will satisfy the parent quadratic
. The “base” case will satisfy the parent quadratic ![]() , while two other cases satisfy
, while two other cases satisfy ![]() — meaning the absolute values are not absolutely necessary after all. However, the way the proof proceeds is slightly different, depending on the presence or absence of absolute values.
— meaning the absolute values are not absolutely necessary after all. However, the way the proof proceeds is slightly different, depending on the presence or absence of absolute values.
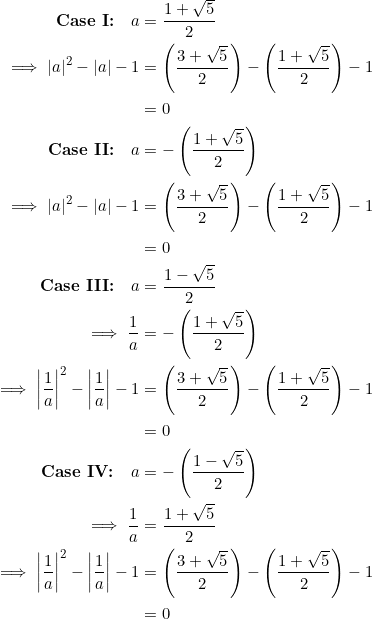
Let ![]() be the slopes of the sides of a right isosceles triangle, with the hypotenuse having slope
be the slopes of the sides of a right isosceles triangle, with the hypotenuse having slope ![]() . PROVE that
. PROVE that ![]() or
or ![]() .
.
In view of example 5, there are also four cases here: ![]() or
or ![]() .
.

Alternative construct
Sometime in the future, we’ll feature our own version of the geometric mean theorem. For now, what to recall is that in any right triangle, the altitude ![]() (from the
(from the ![]() vertex) to the hypotenuse divides the hypotenuse into parts
vertex) to the hypotenuse divides the hypotenuse into parts ![]() and
and ![]() such that
such that
![]()
Since any triangle with side-slopes in geometric progression can be viewed as a clone of the right triangle, we have the following analogue
![]()
where ![]() is the altitude to the side whose slope is
is the altitude to the side whose slope is ![]() (and the altitude divides that side into two parts
(and the altitude divides that side into two parts ![]() and
and ![]() ). Furthermore we have this relationship:
). Furthermore we have this relationship:
(7) ![]()
Remember the name: silvery ratio.
Let ![]() be the slopes of sides
be the slopes of sides ![]() in
in ![]() . PROVE that if the altitude to the side
. PROVE that if the altitude to the side ![]() divides
divides ![]() in the ratio
in the ratio ![]() , then the common ratio
, then the common ratio ![]() or
or ![]() , where
, where ![]() is the golden ratio.
is the golden ratio.
Interesting scenes. Put ![]() in equation (7) and set
in equation (7) and set ![]() :
:
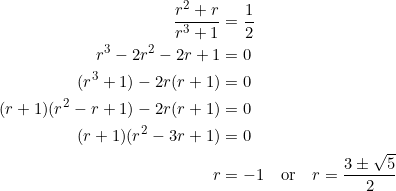
The value ![]() is unacceptable due to slope considerations. So we take
is unacceptable due to slope considerations. So we take ![]() . Then:
. Then:
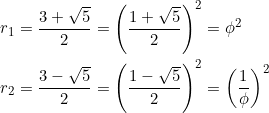
All too familiar by now.
Artificial case
What we get in our next example is not quite the golden ratio, but its made-up “multiple”.
Solve the rational equation ![]() .
.
The left member of the above equation is that sumptuous sum we formed not long after the summer. It should now be common due to how many times it’s been summoned.
Clear fractions: ![]() . Combine like terms:
. Combine like terms: ![]() . Divide through by the common factor
. Divide through by the common factor ![]() :
: ![]() . Assume two quadratic factors of the form
. Assume two quadratic factors of the form ![]() so that, after expanding the right side and comparing coefficients, we have:
so that, after expanding the right side and comparing coefficients, we have:
![]()
We’ll now solve the linear-quadratic system ![]() .
.
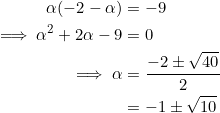
You can already see something close to that golden ratio thing.
![]()
And so
![]()
The first two zeros are got from
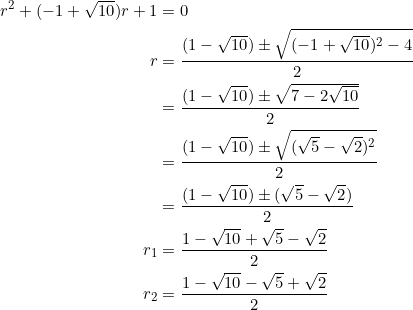
The third and fourth zeros are got from
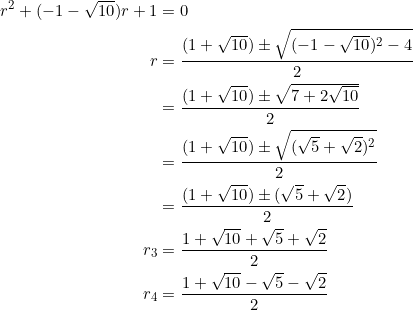
Notice that the roots may be re-written:
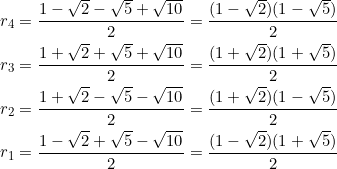
making them “multiples” of the golden ratio and its reciprocal.
Associated converse
Compare — and combine — the example below with example 2.
Suppose that ![]() has sides
has sides ![]() with slopes
with slopes ![]() . If
. If ![]() and
and ![]() (or
(or ![]() ), PROVE that
), PROVE that ![]() is a right triangle.
is a right triangle.
Suppose that ![]() and
and ![]() . Since the slope of side
. Since the slope of side ![]() is
is ![]() , the slope of the median from
, the slope of the median from ![]() to it will be
to it will be ![]() . This median is actually an altitude, due to the
. This median is actually an altitude, due to the ![]() condition. We then have:
condition. We then have:
(8) ![]()
Claim: ![]() , which will ensure that
, which will ensure that ![]() . Isolate
. Isolate ![]() from equation (8) and use a few re-arrangements of the quadratic equation
from equation (8) and use a few re-arrangements of the quadratic equation ![]() repeatedly:
repeatedly:
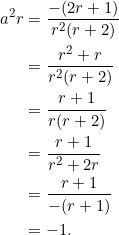
Suppose now that ![]() and
and ![]() . The median from
. The median from ![]() is then an altitude; and its slope being
is then an altitude; and its slope being ![]() means that
means that
(9) ![]()
As before, we claim that ![]() ; that is,
; that is, ![]() (this will ensure that
(this will ensure that ![]() ). From (9) isolate
). From (9) isolate ![]() :
:
![]()
Multiply both sides by ![]() and maneuver the equation
and maneuver the equation ![]() , like so:
, like so:
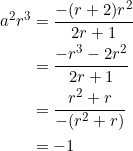
We’ve proved: in ![]() with slopes
with slopes ![]() for sides
for sides ![]() and
and ![]() (or
(or ![]() ), one has
), one has ![]() if and only if the triangle is a right triangle.
if and only if the triangle is a right triangle.
Gold.
Takeaway
For any triangle with sides ![]() having slopes in geometric progression
having slopes in geometric progression ![]() , the following statements are equivalent:
, the following statements are equivalent:

 or
or 
 or
or 
 or
or 
 or
or  or
or  or
or  , where
, where  is the golden ratio
is the golden ratio- the common ratio
 is that of a right isosceles triangle (or that of its “look-alike”)
is that of a right isosceles triangle (or that of its “look-alike”)
Tasks
- (Golden Sum) Consider
 , a sum that should now become common due to the several times it has been summoned.
, a sum that should now become common due to the several times it has been summoned.
- PROVE that the numerator factors as
 .
. - Hence, deduce that
 , where
, where  is the golden ratio.
is the golden ratio.
- PROVE that the numerator factors as
- (Golden State) Find coordinates for the vertices of a triangle with slopes in geometric progression in which:
- the area is

- one of the side-slopes is
 .
.
(Note that the two parts of this question are completely separate/independent, and several answers are possible for each one.)
- the area is
- (Golden Equations) Let
 be the golden ratio. PROVE that:
be the golden ratio. PROVE that:




(The next middle coefficient is . Be bold and go further.)
. Be bold and go further.)
- (Golden Difference) Let
 be the slopes of sides
be the slopes of sides  in
in  .
.
- If
 , PROVE that there is a point
, PROVE that there is a point  on
on  , a point
, a point  on
on  , and a point
, and a point  on
on  such that the slopes of the sides of
such that the slopes of the sides of  form an arithmetic progression with common difference
form an arithmetic progression with common difference  .
. - If
 above and
above and  is the golden ratio, PROVE that
is the golden ratio, PROVE that  is also the golden ratio.
is also the golden ratio.
(The points are all internal points when
are all internal points when  . The situation is even more interesting when
. The situation is even more interesting when  , as the points now become external.)
, as the points now become external.)
- If
- (Golden Mistake) Let
 be the slopes of the sides of a triangle. Suppose that the equations
be the slopes of the sides of a triangle. Suppose that the equations  and
and  both hold.
both hold.
- PROVE that

- Deduce that the original equations are inconsistent.
(This would have been a different way of deriving the golden ratio, if the equations were consistent).
- PROVE that
- Let
 be such that the slopes of sides
be such that the slopes of sides  are
are  , respectively. If the common ratio
, respectively. If the common ratio  satisfies
satisfies  , PROVE that:
, PROVE that:
- Let
 be such that the slopes of sides
be such that the slopes of sides  are
are  , respectively. If the common ratio
, respectively. If the common ratio  satisfies
satisfies  , PROVE that:
, PROVE that:


 (Compare with the previous question.)
(Compare with the previous question.)
- Let
 be such that the slopes of sides
be such that the slopes of sides  are
are  , respectively. If the common ratio
, respectively. If the common ratio  satisfies
satisfies  , PROVE that:
, PROVE that:
- Let
 be such that the slopes of sides
be such that the slopes of sides  are
are  , respectively. If the common ratio
, respectively. If the common ratio  satisfies
satisfies  , PROVE that:
, PROVE that:


 (Compare the “look-alikes” in 8 and 9.)
(Compare the “look-alikes” in 8 and 9.)
- If
 , PROVE that
, PROVE that  . (Notice how the squaring operation “distributes” over addition. Strange, eh?)
. (Notice how the squaring operation “distributes” over addition. Strange, eh?)