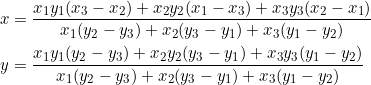New points
Marked below are four points ![]() associated with any
associated with any ![]() :
:
![]() is a diameter of the circumcircle of
is a diameter of the circumcircle of ![]() , while
, while ![]() is a diameter of the nine-point circle of
is a diameter of the nine-point circle of ![]() . Notice that the Euler line
. Notice that the Euler line ![]() of the parent
of the parent ![]() turns out to be a median in
turns out to be a median in ![]() , just as are
, just as are ![]() and
and ![]() .
.
Part of our goal for ![]() is a detailed discussion of these four points, although the discussion will not follow a linear fashion. For now, we’ll first consider
is a detailed discussion of these four points, although the discussion will not follow a linear fashion. For now, we’ll first consider ![]() — in a bid to deliver on the promise made here last year (see the comment preceding example 5 there).
— in a bid to deliver on the promise made here last year (see the comment preceding example 5 there).
Let ![]() ,
, ![]() ,
, ![]() be the vertices of the parent
be the vertices of the parent ![]() . Relative to these vertices,
. Relative to these vertices, ![]() has coordinates:
has coordinates:
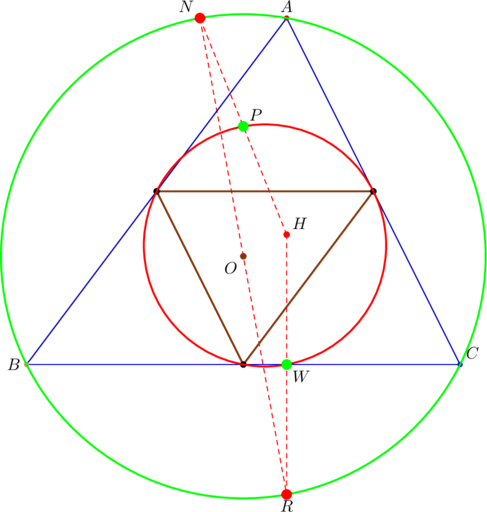
(1) 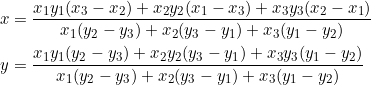
Observe that ![]() is a (horizontal and vertical) translation of the orthocenter of the parent
is a (horizontal and vertical) translation of the orthocenter of the parent ![]() . Also, the “common denominator” in (1) above
. Also, the “common denominator” in (1) above
![]()
is twice the area of ![]() ; as a result,
; as a result,
![]()
and so no ![]() orries about dividing by zero: point
orries about dividing by zero: point ![]() is
is ![]() ell defined. Al
ell defined. Al![]() ays.
ays.
Nice properties
Let’s enumerate some of the properties of point ![]() :
:
- it lies on the nine-point circle of the parent

- it is a point of concurrency of certain line segments (to be featured in the future)
- if a right triangle has legs with slopes
 , then the point
, then the point  coincides with the circumcenter of the right triangle
coincides with the circumcenter of the right triangle - if a right triangle has legs parallel to the coordinate axes (slopes
 ), then the point
), then the point  coincides with the orthocenter of the right triangle
coincides with the orthocenter of the right triangle - if the end points of any side of a triangle are joined to
 , the resulting triangle has slopes in geometric progression (so long as the parent triangle has proper slopes
, the resulting triangle has slopes in geometric progression (so long as the parent triangle has proper slopes  )
) - if any vertex of a triangle is joined to
 and the orthocenter, then the resulting triangle has slopes in geometric progression (so long as the parent triangle has proper slopes
and the orthocenter, then the resulting triangle has slopes in geometric progression (so long as the parent triangle has proper slopes  )
)
You get the gist: our favourite from the above list are the last two. At least.
Numerical problems
Our next move today is to emphasize the first and second to last properties listed above through numerous, numerical instances. As such, the examples below are repetitive; please bear with us.
Consider ![]() with vertices at
with vertices at ![]() ,
, ![]() , and
, and ![]() . PROVE that the point
. PROVE that the point ![]() lies on the nine-point circle of
lies on the nine-point circle of ![]() .
.
Among the points through which the nine-point circle passes are the midpoints of the sides of the parent triangle. In the present case, the midpoints of sides ![]() are
are ![]() , respectively. They are the points
, respectively. They are the points ![]() shown in the diagram below.
shown in the diagram below.
Behind the scenes, we’ve calculated the original triangle’s circumcenter and orthocenter; they are the points ![]() and
and ![]() , respectively.
, respectively.
Let ![]() the center of the nine-point circle. It is the midpoint of the circumcenter and orthocenter of the parent triangle, like so:
the center of the nine-point circle. It is the midpoint of the circumcenter and orthocenter of the parent triangle, like so:
![]()
Lastly, we show that ![]() . By definition we already have
. By definition we already have ![]() .
.
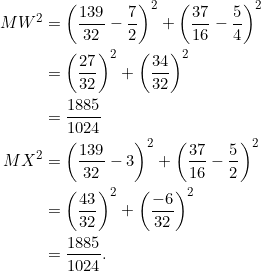
Since ![]() , we conclude that
, we conclude that ![]() is on the nine-point circle of
is on the nine-point circle of ![]() .
.
Calendar fact: In terms of dates, both 1024 and 1885 share something in common. January 14, 1024=January 14, 1885=Wednesday.
Consider ![]() with vertices at
with vertices at ![]() ,
, ![]() , and
, and ![]() . Let
. Let ![]() be the point
be the point ![]() . PROVE that the slopes of the sides of
. PROVE that the slopes of the sides of ![]() ,
, ![]() , and
, and ![]() form geometric progressions (in each case, the geometric mean is the slope of one side of the parent triangle
form geometric progressions (in each case, the geometric mean is the slope of one side of the parent triangle ![]() ).
).
As you’ll recall, the point ![]() is on nine-point cirlce of
is on nine-point cirlce of ![]() .
.
Observe that the slopes of the sides of ![]() are
are ![]() . They form an arithmetic progression, but not a geometric progression. However, our result holds regardless of any pattern of slopes in the parent triangle.
. They form an arithmetic progression, but not a geometric progression. However, our result holds regardless of any pattern of slopes in the parent triangle.
![]() ith
ith ![]() given as
given as ![]() and the original vertices
and the original vertices ![]() ,
, ![]() ,
, ![]() , we can calculate the slopes of the sides of
, we can calculate the slopes of the sides of ![]() ,
, ![]() , and
, and ![]() :
:
- for
 , the side-slopes are
, the side-slopes are  ,
,  ,
,  ; they form a geometric progression with common ratio
; they form a geometric progression with common ratio 
- for
 , the side-slopes are
, the side-slopes are  ,
,  ,
,  ; they form a geometric progression with common ratio
; they form a geometric progression with common ratio 
- for
 , the side-slopes are
, the side-slopes are  ,
,  ,
,  ; they form a geometric progression with
; they form a geometric progression with 
Consider ![]() with vertices at
with vertices at ![]() ,
, ![]() , and
, and ![]() . PROVE that the point
. PROVE that the point ![]() lies on the nine-point circle of
lies on the nine-point circle of ![]()
The midpoints of the sides of ![]() are
are ![]() ,
, ![]() , and
, and ![]() , as shown below:
, as shown below:
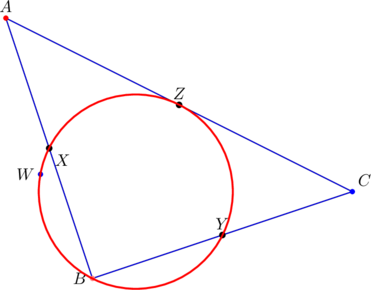
Since the parent ![]() is right-angled at
is right-angled at ![]() , its orthocenter is
, its orthocenter is ![]() and its circumcenter is
and its circumcenter is ![]() , the midpoint of the hypotenuse. Thus, the center of the nine-point circle is
, the midpoint of the hypotenuse. Thus, the center of the nine-point circle is ![]() , say.
, say.
We check that ![]() :
:
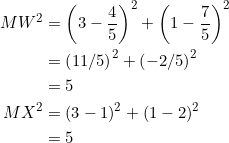
Thus, the point ![]() is on the nine-point circle of
is on the nine-point circle of ![]() .
.
Consider ![]() with vertices at
with vertices at ![]() ,
, ![]() , and
, and ![]() . Let
. Let ![]() be the point
be the point ![]() . PROVE that the slopes of the sides of
. PROVE that the slopes of the sides of ![]() ,
, ![]() , and
, and ![]() form geometric progressions.
form geometric progressions.
Here’s a diagram showing ![]() ,
, ![]() , and
, and ![]() :
:
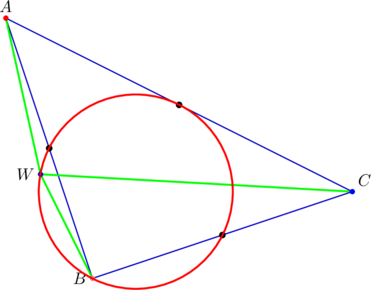
![]() ith
ith ![]() given as
given as ![]() and the original vertices
and the original vertices ![]() ,
, ![]() ,
, ![]() , we can calculate the slopes of the sides of
, we can calculate the slopes of the sides of ![]() ,
, ![]() , and
, and ![]() :
:
- for
 , the side-slopes are
, the side-slopes are  ,
,  ,
,  ; they form a geometric progression with common ratio
; they form a geometric progression with common ratio 
- for
 , the side-slopes are
, the side-slopes are  ,
,  ,
,  ; they form a geometric progression with common ratio
; they form a geometric progression with common ratio 
- for
 , the side-slopes are
, the side-slopes are  ,
,  ,
,  ; they form a geometric progression with
; they form a geometric progression with  .
.
Consider ![]() with vertices at
with vertices at ![]() ,
, ![]() , and
, and ![]() . PROVE that the point
. PROVE that the point ![]() lies on the nine-point circle of
lies on the nine-point circle of ![]()
Behind the scenes, we’ve calculated the parent triangle’s circumcenter and orthocenter; they’re the points ![]() and
and ![]() , respectively. Thus, the center of the nine-point circle is
, respectively. Thus, the center of the nine-point circle is ![]() , say.
, say.
The nine-point circle passes through the midpoints ![]() ,
, ![]() ,
, ![]() of the parent triangle.
of the parent triangle.
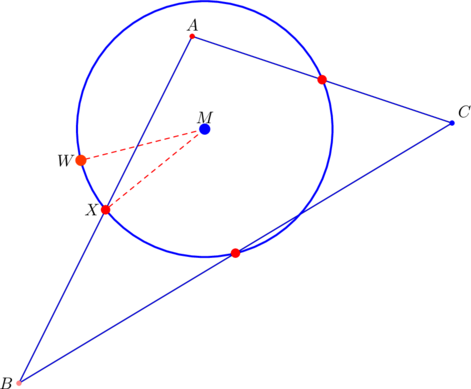
We check that ![]() :
:
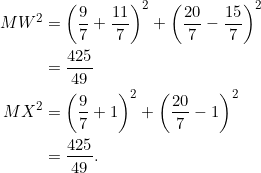
Consider ![]() with vertices at
with vertices at ![]() ,
, ![]() , and
, and ![]() . Let
. Let ![]() be the point
be the point ![]() . PROVE that the slopes of the sides of
. PROVE that the slopes of the sides of ![]() ,
, ![]() , and
, and ![]() form geometric progressions.
form geometric progressions.
- The slopes of the sides of
 are
are  they form a geometric progression with common ratio
they form a geometric progression with common ratio  .
. - The slopes of the sides of
 are
are  they form a geometric progression with common ratio
they form a geometric progression with common ratio  .
. - The slopes of the sides of
 are
are  they form a geometric progression with common ratio
they form a geometric progression with common ratio  .
.
Consider ![]() with vertices at
with vertices at ![]() ,
, ![]() , and
, and ![]() . PROVE that the point
. PROVE that the point ![]() lies on the nine-point circle of
lies on the nine-point circle of ![]() .
.
The midpoints of sides ![]() ; they are
; they are ![]() , respectively. They are the points
, respectively. They are the points ![]() shown in the diagram below.
shown in the diagram below.
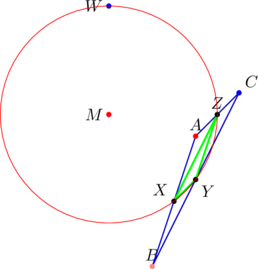
Behind the scenes, we’ve calculated the original triangle’s circumcenter and orthocenter; they are the points ![]() and
and ![]() , respectively. It follows that the center of the nine-point circle in this case is the point
, respectively. It follows that the center of the nine-point circle in this case is the point ![]() , denoted
, denoted ![]() in the diagram above.
in the diagram above.
Now we check that ![]() . Again, it suffices to check
. Again, it suffices to check ![]() :
:
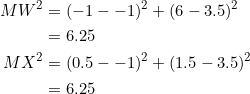
Thus, ![]() lies on the nine-point circle of
lies on the nine-point circle of ![]() .
.
Consider ![]() with vertices at
with vertices at ![]() ,
, ![]() , and
, and ![]() . Let
. Let ![]() be the point
be the point ![]() . PROVE that the slopes of the sides of
. PROVE that the slopes of the sides of ![]() ,
, ![]() , and
, and ![]() form geometric progressions.
form geometric progressions.
As you’ll recall, the point ![]() is on the nine-point circle of the parent triangle
is on the nine-point circle of the parent triangle ![]() .
.
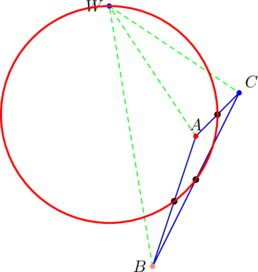
Observe that the slopes of the sides of ![]() are
are ![]() . They form an arithmetic progression, but not a geometric progression.
. They form an arithmetic progression, but not a geometric progression.
- The slopes of the sides of
 are
are  they form a geometric progression with common ratio
they form a geometric progression with common ratio  (remember the name: a peach).
(remember the name: a peach). - The slopes of the sides of
 are
are  they form a geometric progression with common ratio
they form a geometric progression with common ratio  .
. - The slopes of the sides of
 are
are  they form a geometric progression with common ratio
they form a geometric progression with common ratio  .
.
Consider ![]() with vertices at
with vertices at ![]() ,
, ![]() , and
, and ![]() . Find coordinates for a point
. Find coordinates for a point ![]() for which the slopes of the sides of
for which the slopes of the sides of ![]() ,
, ![]() , and
, and ![]() form three separate geometric progressions.
form three separate geometric progressions.
Use equation (1) with ![]() ,
, ![]() , and
, and ![]() :
:
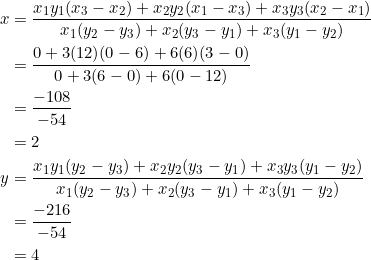
The desired point is ![]() .
.
![]() ith the point
ith the point ![]() and the original coordinates
and the original coordinates ![]() ,
, ![]() ,
, ![]() , the slopes of the sides of each of
, the slopes of the sides of each of ![]() ,
, ![]() , and
, and ![]() can be calculated:
can be calculated:
- the slopes of the sides of
 are
are  ; they form a geometric progression with common ratio
; they form a geometric progression with common ratio 
- the slopes of the sides of
 are
are  ; they form a geometric progression with common ratio
; they form a geometric progression with common ratio 
- the slopes of the sides of
 are
are  ; they form a geometric progression with common ratio
; they form a geometric progression with common ratio  .
.
There’s an additional point ![]() orth noting here. If one calculates the slopes from
orth noting here. If one calculates the slopes from ![]() to each of the vertices
to each of the vertices ![]() ,
, ![]() ,
, ![]() , one obtains
, one obtains
![]()
a geometric progression with common ratio ![]() . This only happens in some specific situations (see the exercises).
. This only happens in some specific situations (see the exercises).
Given ![]() with vertices at
with vertices at ![]() ,
, ![]() ,
, ![]() , verify that the point
, verify that the point ![]() found in the previous example lies on the nine point circle of
found in the previous example lies on the nine point circle of ![]() .
.
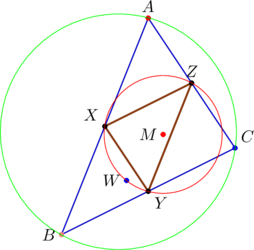
The midpoints of the sides of ![]() are
are ![]() ,
, ![]() ,
, ![]() ; they’re shown (in the big circle) below as red bullet points:
; they’re shown (in the big circle) below as red bullet points:
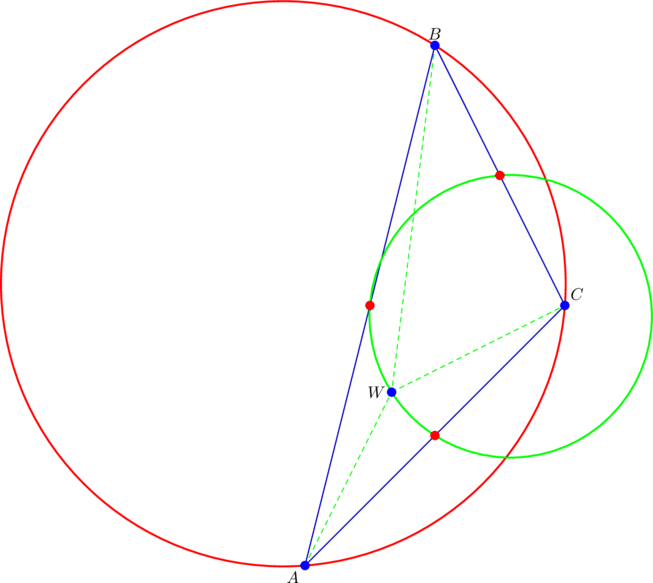
Behind the scenes, we’ve calculated the circumcenter and the orthocenter of ![]() ; they are the points
; they are the points ![]() and
and ![]() , respectively. Thus, the center of the nine-point circle is
, respectively. Thus, the center of the nine-point circle is ![]() , say.
, say.
We now check that ![]() :
:
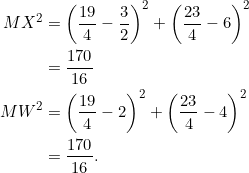
Boom.
Takeaway
Triangles with slopes in geometric progressions are very nice objects, at least because of the “algebra” that their theory brings along. However, even if the slopes of the sides of a triangle do not form a geometric progression (sighs), there’s a ![]() ay around it:
ay around it:
- if the parent triangle has a side parallel to any of the axes, relax — already done last March.
- if the parent triangle
 has no side parallel to the coordinate axes, call
has no side parallel to the coordinate axes, call  with coordinates
with coordinates
(2)

and obtain triangles
 ,
,  ,
,  whose side-slopes form three separate geometric progressions. (Alternatively, one can also use
whose side-slopes form three separate geometric progressions. (Alternatively, one can also use  and the orthocenter
and the orthocenter  . Then the slopes of the sides of triangles
. Then the slopes of the sides of triangles  ,
,  ,
,  form three separate geometric progressions.)
form three separate geometric progressions.)
Tasks
Throughout, any mention of ![]() refers to the point with coordinates given by equation (1) or (2). Unless otherwise specified, assume where necessary that an arbitrary triangle
refers to the point with coordinates given by equation (1) or (2). Unless otherwise specified, assume where necessary that an arbitrary triangle ![]() has vertices at
has vertices at ![]() ,
, ![]() , and
, and ![]() .
.
- (Separate character) Verify that the point
 is not any of the nine traditional points through which the nine-point circle passes. Under normal circumstances.
is not any of the nine traditional points through which the nine-point circle passes. Under normal circumstances. - (Special case) Let
 be such that
be such that  . If the slopes of the legs
. If the slopes of the legs  and
and  are
are  , PROVE that
, PROVE that  coincides with the mid-point of
coincides with the mid-point of  (that is, the circumcenter of
(that is, the circumcenter of  . Also see exercise 8 below).
. Also see exercise 8 below). - (Special case) If
 , PROVE that
, PROVE that  is precisely the foot of the altitude from vertex
is precisely the foot of the altitude from vertex  .
. - (Shortcut) In
 , let
, let  be the slopes of sides
be the slopes of sides  . PROVE that:
. PROVE that:
 has coordinates
has coordinates 
- the slopes from
 to the vertices form a geometric progression
to the vertices form a geometric progression 
(The best setting for is
is  hen the slopes of the sides of the parent triangle form a geometric progression.)
hen the slopes of the sides of the parent triangle form a geometric progression.)
- (Shortcut) In
 , let
, let  be the slopes of sides
be the slopes of sides  , where
, where  . PROVE that:
. PROVE that:
 has coordinates
has coordinates 
- the slopes from
 to the vertices are
to the vertices are 
- the slopes from
 to the vertices form a geometric progression if
to the vertices form a geometric progression if  or
or  or
or 
(In each case, the common ratio is always positive — in fact, a “square”.) - the slopes from
 to the vertices form an arithmetic progression if
to the vertices form an arithmetic progression if  .
.
(Incidentally, the common difference of the resulting arithmetic progression is equal to , depending on how it’s arranged.)
, depending on how it’s arranged.)
- (Six colleagues) Let
 be the orthocenter of
be the orthocenter of  and let
and let  be as given in equation (1). PROVE that the six statements below are equivalent:
be as given in equation (1). PROVE that the six statements below are equivalent:

 coincides with one of the vertices of
coincides with one of the vertices of 
 has two sides parallel to the coordinate axes
has two sides parallel to the coordinate axes- the slopes of the three medians form a geometric progression with common ratio

- the slopes of the three medians form an arithmetic progression with common difference
 (
( first term)
first term) - one side is parallel to the
 -axis and another side and the median to it have opposite slopes (e.g.
-axis and another side and the median to it have opposite slopes (e.g.  and
and  ).
).
- (HOW come?) In
 , let the orthocenter and circumcenter be
, let the orthocenter and circumcenter be  and
and  , respectively, and let
, respectively, and let  be as given in (1). If the slopes of sides
be as given in (1). If the slopes of sides  are
are  in that order, PROVE that:
in that order, PROVE that:
- the circumcenter shares the same
 -coordinate as vertex
-coordinate as vertex 
- the slopes of the sides of
 form an arithmetic progression
form an arithmetic progression
(One of the reasons we chose as a label for one of our four points
as a label for one of our four points  — rather than
— rather than  maybe — was because we had this triangle
maybe — was because we had this triangle  in view.)
in view.)
- the circumcenter shares the same
- Are the following statements equivalent?
 is the midpoint of
is the midpoint of  ; that is,
; that is, 
- either
 is isosceles with side
is isosceles with side  parallel to the
parallel to the  -axis and
-axis and  , or two sides of
, or two sides of  have opposite slopes
have opposite slopes - the area of
 is
is  or
or  .
.
(This exercise shows that in some situations, behaves like the circumcenter of a right triangle which occurs at the midpoint of the hypotenuse.)
behaves like the circumcenter of a right triangle which occurs at the midpoint of the hypotenuse.)
- Consider a right triangle in which none of the sides is parallel to the coordinate axes. PROVE that the slope from
 to the
to the  vertex is the reciprocal of the slope of the hypotenuse.
vertex is the reciprocal of the slope of the hypotenuse. - PROVE that
 is a both a horizontal and a vertical translation of the orthocenter
is a both a horizontal and a vertical translation of the orthocenter  of the parent
of the parent  .
.