Basically, geometric slopes involve three numbers ![]() that are in geometric progression — like
that are in geometric progression — like ![]() — but at the same time are slopes of the sides of a triangle. Note that this is not a standard terminology; we’re using it here to keep the title short.
— but at the same time are slopes of the sides of a triangle. Note that this is not a standard terminology; we’re using it here to keep the title short.
We present two “propositions” that describe precisely when the slopes of the sides of a triangle form a geometric progression.
Notation and characterization
In ![]() , let’s denote the slopes of the three medians from vertices
, let’s denote the slopes of the three medians from vertices ![]() by
by ![]() , respectively. Similarly, the slopes of sides
, respectively. Similarly, the slopes of sides ![]() will be denoted by
will be denoted by ![]() .
.
If ![]() , PROVE that
, PROVE that ![]() , where
, where ![]() has vertices at
has vertices at ![]() .
.
![]() is the slope of the line segment joining
is the slope of the line segment joining ![]() to the midpoint of
to the midpoint of ![]() ;
; ![]() is the slope of side
is the slope of side ![]() . So we have:
. So we have:
![]()
Now, if ![]() , write
, write ![]() . Clear fractions:
. Clear fractions:
![]()
Expand and combine like terms:
![]()
Obtain ![]() , from which
, from which ![]() can be isolated as:
can be isolated as:
![]()
Example 2 (First proposition)
For ![]() with vertices at
with vertices at ![]() and non-zero side slopes, PROVE that the slopes of sides
and non-zero side slopes, PROVE that the slopes of sides ![]() form a geometric progression if, and only if,
form a geometric progression if, and only if, ![]() .
.
In other words, once one of the medians has a slope that is the negative of the slope of the side that contains its “foot”, then the slopes of the sides of the triangle form a geometric progression.
The non-zero requirement for the slopes of the sides is crucial. See Example 3 below. Also, click here for a pdf version of some of the equations in this post.
Suppose that ![]() ; we’ll show that the slopes of sides
; we’ll show that the slopes of sides ![]() (namely
(namely ![]() ) form a geometric progression. It suffices to show that
) form a geometric progression. It suffices to show that ![]() .
.
Since ![]() , we can use
, we can use ![]() from Example 1 and obtain
from Example 1 and obtain ![]() :
:
![Rendered by QuickLaTeX.com \begin{equation*} \boldmath\begin{split} &=\scriptstyle\frac{(y_1-y_2)(y_3-y_1)}{\Big[\frac{x_2(y_1-y_2)+x_3(y_3-y_1)}{y_3-y_2}-x_2\Big]\Big[x_3-\Big(\frac{x_2(y_1-y_2)+x_3(y_3-y_1)}{y_3-y_2}\Big)\Big]}\\ &=\scriptscriptstyle\frac{(y_1-y_2)(y_3-y_1)(y_3-y_2)^2}{[x_2(y_1-y_2)+x_3(y_3-y_1)-x_2(y_3-y_2)][x_3(y_3-y_2)-x_2(y_1-y_2)-x_3(y_3-y_2)]}\\ &=\scriptstyle\frac{(y_1-y_2)(y_3-y_1)(y_3-y_2)^2}{[x_2(y_1-y_2-y_3+y_2)+x_3(y_3-y_1)][x_3(y_3-y_2-y_3+y_1)-x_2(y_1-y_2)]}\\ &=\frac{(y_1-y_2)(y_3-y_1)(y_3-y_2)^2}{(x_3-x_2)(y_3-y_1)(x_3-x_2)(y_1-y_2)}\\ &=\Big(\frac{y_3-y_2}{x_3-x_2}\Big)^2. \end{split} \end{equation*}](https://blog.fridaymath.com/wp-content/ql-cache/quicklatex.com-20b83f5bc95c058fb47d32caecb96070_l3.png)
![]() , and so the slopes
, and so the slopes ![]() form a geometric progression. The converse was proved in Example 8 of our post on January 28, 2020.
form a geometric progression. The converse was proved in Example 8 of our post on January 28, 2020.
Consider the right triangle ![]() with vertices at
with vertices at ![]() . PROVE that the slope of the median from vertex
. PROVE that the slope of the median from vertex ![]() is the negative of the slope of the hypotenuse
is the negative of the slope of the hypotenuse ![]() .
.
Using the given coordinates and the mid-point formula, the mid-point of the hypotenuse ![]() is
is
![]()
and so the slope of the median from vertex ![]() is
is
![]()
Now, the slope of the hypotenuse ![]() is
is
![]()
which is the negative of the slope of the median from vertex ![]() .
.
Example 4 (Second proposition)
In ![]() , PROVE that
, PROVE that ![]() if, and only if,
if, and only if, ![]() , where
, where ![]() is the length of the median from vertex
is the length of the median from vertex ![]() and the triangle’s vertices are located at
and the triangle’s vertices are located at ![]() .
.
Consequently, we obtain a second characterization of slopes in geometric progression.
First suppose that ![]() . Since
. Since
![]()
![]() .
.
Now, the length ![]() of the median from vertex
of the median from vertex ![]() is the distance from
is the distance from ![]() to the midpoint of
to the midpoint of ![]() :
:
![Rendered by QuickLaTeX.com \begin{equation*} \begin{split} m_{a}^2&=\Big(\frac{x_2+x_3}{2}-x_1\Big)^2+\Big(\frac{y_2+y_3}{2}-y_1\Big)^2\\ &=\Big(\frac{x_2+x_3-2x_1}{2}\Big)^2+\Big(\frac{y_2+y_3-2y_1}{2}\Big)^2\\ &=\frac{1}{4}\Big((x_2+x_3-2x_1)^2+(y_2+y_3-2y_1)^2\Big)\\ &=\frac{1}{4}\Big[(x_2+x_3-2x_1)^2+\Big(-(\frac{y_3-y_2}{x_3-x_2})(x_2+x_3-2x_1)\Big)^2\Big]\\ &=\frac{1}{4}\frac{(x_2+x_3-2x_1)^2}{(x_3-x_2)^2}\Big((x_3-x_2)^2+(y_3-y_2)^2\Big)\\ \therefore m_{a}&=\frac{x_2+x_3-2x_1}{2(x_3-x_2)}\sqrt{(x_3-x_2)^2+(y_3-y_2)^2} \end{split} \end{equation}](https://blog.fridaymath.com/wp-content/ql-cache/quicklatex.com-bab75d3edce50fd16f9de43984768bfe_l3.png)
A little care should be taken pertaining the sign of ![]() , so its absolute value should be used instead.
, so its absolute value should be used instead.
Conversely, suppose that ![]() . Usually,
. Usually, ![]() , in view of the given coordinates. Together with the assumption of the converse, this amounts to:
, in view of the given coordinates. Together with the assumption of the converse, this amounts to:
![Rendered by QuickLaTeX.com \begin{equation*} \begin{split} \Big(\frac{x_2+x_3-2x_1}{2}\Big)^2+\Big(\frac{y_2+y_3-2y_1}{2}\Big)^2&=\Big(\frac{x_2+x_3-2x_1}{2(x_3-x_2)}\sqrt{(x_3-x_2)^2+(y_3-y_2)^2}\Big)^2\\ \Big(\frac{y_2+y_3-2y_1}{2}\Big)^2&=\Big(\frac{x_2+x_3-2x_1}{2(x_3-x_2)}\Big)^2[(x_3-x_2)^2+(y_3-y_2)^2]-\Big(\frac{x_2+x_3-2x_1}{2}\Big)^2\\ \Big(\frac{y_2+y_3-2y_1}{2}\Big)^2&=(x_2+x_3-2x_1)^2\Big(\frac{(x_3-x_2)^2+(y_3-y_2)^2}{4(x_3-x_2)^2}-\frac{1}{4}\Big)\\ \therefore \frac{(y_2+y_3-2y_1)^2}{4}&=\frac{1}{4}(x_2+x_3-2x_1)^2\Big(\frac{y_3-y_2}{x_3-x_2}\Big)^2\\ \Big(\frac{y_2+y_3-2y_1}{x_2+x_3-2x_1}\Big)^2&=\Big(\frac{y_3-y_2}{x_3-x_2}\Big)^2 \end{split} \end{equation}](https://blog.fridaymath.com/wp-content/ql-cache/quicklatex.com-b82bd39114ec948d63dbfcef3a03979e_l3.png)
Extracting square roots, we get ![]() . Since the slope of a median cannot be equal to the slope of the side it meets, we must then take the negative square root, and so
. Since the slope of a median cannot be equal to the slope of the side it meets, we must then take the negative square root, and so ![]() . In terms of our notation, this translates to
. In terms of our notation, this translates to ![]() , or
, or ![]() .
.
![]() (that is, the slope of the median from vertex
(that is, the slope of the median from vertex ![]() is the negative of the slope of side
is the negative of the slope of side ![]() );
);
the (non-zero) slopes of sides ![]() form a geometric progression;
form a geometric progression;
the length of the median from vertex ![]() is
is ![]() .
.
Applying the first proposition
Our first application goes to the right triangle considered in Example 3; it will be the basis of a future post — where we aim to unveil a hidden characteristic in every triangle.
PROVE that the right triangle ![]() with vertices at
with vertices at ![]() contains a “sub-triangle” whose side slopes form a geometric progression with a common ratio of
contains a “sub-triangle” whose side slopes form a geometric progression with a common ratio of ![]() .
.
In view of Example 3, we know that the median from vertex ![]() has a slope that’s the negative of the slope of the hypotenuse
has a slope that’s the negative of the slope of the hypotenuse ![]() . Consider the midpoint of median from
. Consider the midpoint of median from ![]() to
to ![]() , located at
, located at ![]() , say.
, say.
The triangle with vertices ![]() is the desired “sub-triangle”. Indeed, the slopes of its sides are:
is the desired “sub-triangle”. Indeed, the slopes of its sides are:
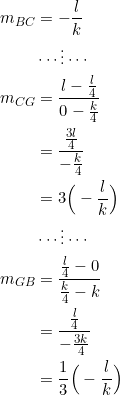
This verifies that the slopes of the “sub-triangle” ![]() form a geometric progression with a common ratio of
form a geometric progression with a common ratio of ![]() .
.
PROVE that if the slopes of the sides of a triangle form a geometric progression (with common ratio ![]() ), then so do the slopes of the three medians, provided
), then so do the slopes of the three medians, provided ![]() (or
(or ![]() ).
).
In Example 7 and Example 8 below, we explain what underlies the restriction ![]() .
.
If ![]() has sides
has sides ![]() with slopes
with slopes ![]() in geometric progression, we’ll prove that the median slopes
in geometric progression, we’ll prove that the median slopes ![]() form a new geometric progression.
form a new geometric progression.
Let the coordinates of ![]() be
be ![]() . We have
. We have
![]()
and
![]()
From our first proposition, ![]() being in geometric progression means that
being in geometric progression means that ![]() , and so
, and so ![]() . That is,
. That is, ![]() . From Example 1,
. From Example 1, ![]() .
.
![Rendered by QuickLaTeX.com \begin{equation*} \begin{split} m_{B}\times m_{C}&=\Big(\frac{y_1+y_3-2y_2}{x_1+x_3-2x_2}\Big)\Big(\frac{y_1+y_2-2y_3}{x_1+x_2-2x_3}\Big)\\ &=\frac{y_1+y_2-2y_3}{\Big[\frac{x_3(y_3-y_1)+x_2(y_1-y_2)}{y_3-y_2}+x_2-2x_3\Big]}\times\frac{y_1+y_3-2y_2}{\Big[\frac{x_3(y_3-y_1)+x_2(y_1-y_2)}{y_3-y_2}+x_3-2x_2\Big]}\\ &=\frac{y_1+y_2-2y_3}{\frac{x_3(y_3-y_1)+x_2(y_1-y_2)+x_2(y_3-y_2)-2x_3(y_3-y_2)}{y_3-y_2}}\times\frac{y_1+y_3-2y_2}{\frac{x_3(y_3-y_1)+x_2(y_1-y_2)+x_3(y_3-y_2)-2x_2(y_3-y_2)}{y_3-y_2}}\\ &=\scriptscriptstyle\frac{(y_1+y_2-2y_3)(y_3-y_2)}{\Big[x_3(y_3-y_1-2y_3+2y_2)+x_2(y_1-y_2+y_3-y_2)\Big]}\times\frac{(y_1+y_3-2y_2)(y_3-y_2)}{\Big[x_3(y_3-y_1+y_3-y_2)+x_2(y_1-y_2-2y_3+2y_2)\Big]}\\ &=\scriptscriptstyle\frac{(y_1+y_2-2y_3)(y_3-y_2)}{[x_3(-y_1-y_3+2y_2)+x_2(y_1+y_3-2y_2)]}\times\frac{(y_1+y_3-2y_2)(y_3-y_2)}{[x_3(-y_1-y_2+2y_3)+x_2(y_1+y_2-2y_3)]}\\ &=\frac{(y_1+y_2-2y_3)(y_3-y_2)}{(x_2-x_3)(y_1+y_3-2y_2)}\times\frac{(y_1+y_3-2y_2)(y_3-y_2)}{(x_2-x_3)(y_1+y_2-2y_3)}\\ &=\Big(\frac{y_3-y_2}{x_3-x_2}\Big)^2\\ &=m_{A}^2 \end{split} \end{equation*}](https://blog.fridaymath.com/wp-content/ql-cache/quicklatex.com-018a1b0039a8f352d12098f79b01a724_l3.png)
So, the median slopes ![]() form a geometric progression, with
form a geometric progression, with ![]() as the geometric mean.
as the geometric mean.
Suppose that the slopes of the sides of a triangle form a geometric progression with a common ratio of ![]() . PROVE that the triangle contains a horizontal median.
. PROVE that the triangle contains a horizontal median.
We’ve given a proof of this before by explicitly determining the coordinates of the vertices in terms of the common ratio ![]() ; here we present a direct approach that avoids row reduction (linear algebra).
; here we present a direct approach that avoids row reduction (linear algebra).
Assume the geometric progression of the slopes is ![]() , where
, where ![]() are the triangle’s vertices. Since the common ratio is
are the triangle’s vertices. Since the common ratio is ![]() , we have:
, we have:
![]()
Isolate ![]() from the first equation:
from the first equation:
![]()
Also, from the second equation, isolating ![]() gives
gives
![]()
Equate the two expressions obtained for ![]() :
:
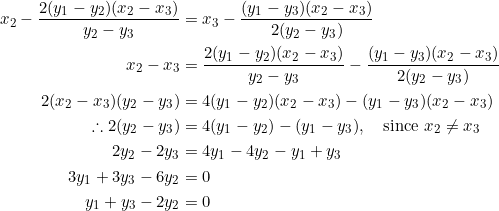
Thus, the slope of the median from vertex ![]() is zero, that is,
is zero, that is, ![]() , giving a horizontal median.
, giving a horizontal median.
Suppose that the slopes of the sides of a triangle form a geometric progression with a common ratio of ![]() . PROVE that the triangle contains a vertical median.
. PROVE that the triangle contains a vertical median.
As in Example 7, the fact the geometric progression has a common ratio of ![]() means we can write:
means we can write:
![]()
We obtain ![]() , from which
, from which
![]()
Also, from ![]() , isolating
, isolating ![]() gives
gives
![]()
Equate the two expressions obtained for ![]() :
:
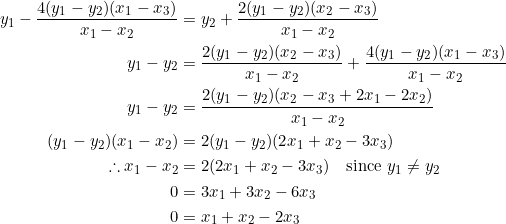
Therefore, the slope of the median from vertex ![]() , given by
, given by ![]() , is undefined, so this median is vertical.
, is undefined, so this median is vertical.
Suppose that ![]() is isosceles and that the slope of the median from the “apex”
is isosceles and that the slope of the median from the “apex” ![]() is
is ![]() . PROVE that the slopes of its sides form a geometric progression.
. PROVE that the slopes of its sides form a geometric progression.
This is based on the fact that the slope of the median from the “apex” of an isosceles triangle is the negative reciprocal of the slope of the base. In particular, if ![]() , then
, then ![]() , giving
, giving ![]() . By our first proposition, this means the slopes of sides
. By our first proposition, this means the slopes of sides ![]() form a geometric progression. Similarly, if
form a geometric progression. Similarly, if ![]() , then
, then ![]() , also giving
, also giving ![]() , and we again obtain a geometric progression for the slopes of sides
, and we again obtain a geometric progression for the slopes of sides ![]() .
.
A numerical problem
![]() has vertices at
has vertices at ![]() . Determine suitable values of
. Determine suitable values of ![]() and
and ![]() for which the slopes of sides
for which the slopes of sides ![]() form a geometric progression.
form a geometric progression.
Using our first proposition, we can tackle this problem by somehow “forcing” a median from side ![]() to have a slope that’s the negative of side
to have a slope that’s the negative of side ![]() ‘s slope. (Note that we can also use Exercise 1 below, which may be easier.)
‘s slope. (Note that we can also use Exercise 1 below, which may be easier.)
Let’s find the equation of this “forced” median. The midpoint of ![]() is
is ![]() , and its slope is
, and its slope is ![]() . So we want a median through
. So we want a median through ![]() with slope
with slope ![]() . Its equation is:
. Its equation is:
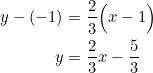
Thus, any point on the line ![]() — except the trio
— except the trio ![]() — will do for the coordinates of vertex
— will do for the coordinates of vertex ![]() . Why exclude these three? First, the point
. Why exclude these three? First, the point ![]() is the midpoint of
is the midpoint of ![]() , so we can’t form a triangle with it. Next, the point
, so we can’t form a triangle with it. Next, the point ![]() shares the same
shares the same ![]() -coordinate with vertex
-coordinate with vertex ![]() , which will make the slope of
, which will make the slope of ![]() zero if
zero if ![]() is chosen as the point
is chosen as the point ![]() . Similarly, we can’t take
. Similarly, we can’t take ![]() for
for ![]() because then
because then ![]() will have the same
will have the same ![]() -coordinate with vertex
-coordinate with vertex ![]() , resulting in an undefined slope.
, resulting in an undefined slope.
With the exclusions out of the way, we can take any other point, say ![]() , as
, as ![]() . Then
. Then ![]() has vertices at
has vertices at ![]() , and the slopes of sides
, and the slopes of sides ![]() become
become
![]()
respectively. They form a geometric progression with a common ratio of ![]() (or
(or ![]() if we reverse the numbers).
if we reverse the numbers).
A few other points on the line ![]() that can be chosen in place of
that can be chosen in place of ![]() — and the corresponding geometric progressions for the slopes of the sides — are listed below:
— and the corresponding geometric progressions for the slopes of the sides — are listed below:
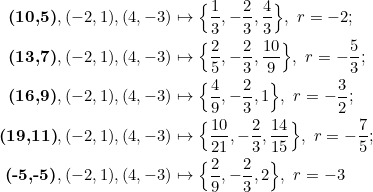
Observe that the choice ![]() yields the same set of geometric progression as our initial choice
yields the same set of geometric progression as our initial choice ![]() .
.
As in, this whole thing is COOL!
Takeaway
In the domain of triangles, the GOAT (Greatest Of All Triangles) is the triangle whose slopes form a geometric progression. No jokes.
That told, our first proposition is the basis for our future application. In particular, what we did for the right triangle in Example 5 will be done for any triangle. As in, A-N-Y!
Tasks
- (Generating formula) Let
 be the coordinates of the vertices of
be the coordinates of the vertices of  . Require that
. Require that  and that
and that  . PROVE that the slopes of sides
. PROVE that the slopes of sides  form a geometric progression if, and only if,
form a geometric progression if, and only if, 
 Thus, in order to obtain coordinates for the vertices of a triangle whose slopes form a geometric progression, begin by selecting “any” five numbers — ensuring that no two
Thus, in order to obtain coordinates for the vertices of a triangle whose slopes form a geometric progression, begin by selecting “any” five numbers — ensuring that no two  s are equal and no two
s are equal and no two  s are equal — then use the above relation to determine the value of the remaining coordinate.
s are equal — then use the above relation to determine the value of the remaining coordinate.
- (Special ratio) Let
 be the coordinates of the vertices of
be the coordinates of the vertices of  . PROVE that:
. PROVE that:
 if, and only if,
if, and only if,  (that is, the medians through
(that is, the medians through  and
and  are perpendicular)
are perpendicular)- if the slopes
 form a geometric progression, then
form a geometric progression, then  if, and only if,
if, and only if,  (that is, the median through
(that is, the median through  is vertical)
is vertical) - if the slopes
 form a geometric progression and
form a geometric progression and  , then the median through
, then the median through  is horizontal
is horizontal - if the slopes
 form a geometric progression and
form a geometric progression and  , then the common ratio of the geometric progression is
, then the common ratio of the geometric progression is 
(If the slopes of the sides of a triangle form a geometric progression, no other value for the common ratio yields the relation ; only
; only  does.)
does.)
- (Half right) Let
 be a triangle in which the slopes
be a triangle in which the slopes  form a geometric progression. PROVE that the acute angle between the median from
form a geometric progression. PROVE that the acute angle between the median from  and side
and side  is
is  if, and only if,
if, and only if,  or
or  .
. - (Pseudo perpendicularity) Suppose that the slopes
 of the sides
of the sides  of
of  form a geometric progression with common ratio
form a geometric progression with common ratio  . Let the lengths of sides
. Let the lengths of sides  be
be  , respectively. PROVE that the following pseudo-pythagorean property holds:
, respectively. PROVE that the following pseudo-pythagorean property holds:  .
.
(If we let , then we obtain a full pythagorean relationship. However,
, then we obtain a full pythagorean relationship. However,  is unacceptable for a geometric progression. Note that this doesn’t imply the impossibility of having right triangles with slopes in geometric progression; there are actually many of them — with an appropriately chosen first term and a negative common ratio. Now, if we let
is unacceptable for a geometric progression. Note that this doesn’t imply the impossibility of having right triangles with slopes in geometric progression; there are actually many of them — with an appropriately chosen first term and a negative common ratio. Now, if we let  , we get
, we get  , a peach.)
, a peach.) - Suppose that the slopes of a right triangle form a geometric progression. PROVE that the slope of the hypotenuse cannot be the geometric mean of the progression.
(For a change, attempt this exercise without recourse to perpendicular slopes. Use our second proposition (Example 4) and the fact that the length of the median to the hypotenuse is half of the length of the hypotenuse.) - Let
 be the coordinates of the vertices of an equilateral
be the coordinates of the vertices of an equilateral  . If the slopes of sides
. If the slopes of sides  form a geometric progression, prove that
form a geometric progression, prove that  , or
, or 
(Note the order of the slopes.)  has vertices at
has vertices at  . Find three different pairs
. Find three different pairs  for which the slopes of the sides form a geometric progression with a common ratio of
for which the slopes of the sides form a geometric progression with a common ratio of  .
.- (Three possibilities) Let
 be the coordinates of the vertices of a triangle. If the slopes of the sides form a geometric progression, PROVE that at least one of these three is true:
be the coordinates of the vertices of a triangle. If the slopes of the sides form a geometric progression, PROVE that at least one of these three is true:
 ;
; ;
; .
.
(Use the generating formula.)
- PROVE that every right triangle
 with legs
with legs  and
and  on — or parallel to — the coordinate axes contains a “sub-triangle”
on — or parallel to — the coordinate axes contains a “sub-triangle”  that has the following property: the length of the median from vertex
that has the following property: the length of the median from vertex  is one-fourth the length of the hypotenuse
is one-fourth the length of the hypotenuse  ; that is,
; that is,  .
.
(For instance, consider the “sub-triangle” we constructed in Example 5.) - Find suitable choice of coordinates for the vertices of
 that has the property that
that has the property that  , where
, where  is the length of the median from vertex
is the length of the median from vertex  and
and  is the length of side
is the length of side  .
.
(Consider the case where the slopes of sides form a geometric progression with a common ratio of
form a geometric progression with a common ratio of  .)
.)