Triangles whose side slopes form a geometric progression are very nice objects, and a very special subset of such triangles is our subject for today.
Coordinates for equilateral triangles
Just recently, we paid a visit to the place where equilateral triangles live in the Cartesian plane; consequently, we begin by giving you their full “address”, so you can also locate them without stress, without pain.
Example 1
Let ![]() be a triangle. PROVE that the following are equivalent:
be a triangle. PROVE that the following are equivalent:
 is equilateral with length
is equilateral with length  ;
;- its vertices are located at
 ,
,  ,
, 
![]() is some parameter that can be thought of as the angle that the “base” of the triangle makes with the positive
is some parameter that can be thought of as the angle that the “base” of the triangle makes with the positive ![]() -axis.
-axis.
So a complete description of the coordinates of the vertices of an equilateral triangle requires three things: a starting point ![]() , a fixed length
, a fixed length ![]() , and the “base” inclination
, and the “base” inclination ![]() . In the traditional case, these correspond to
. In the traditional case, these correspond to ![]() and
and ![]() , respectively.
, respectively.
Let’s first prove that any triangle having the given coordinates is equilateral. We’ll use the trig identity ![]() and the distance formula:
and the distance formula:
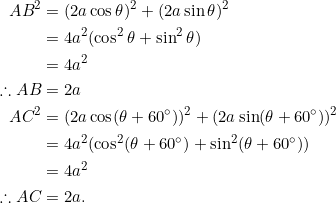
It now remains side ![]() ; we’ll compute its length in two steps, starting with the “run” (difference of the
; we’ll compute its length in two steps, starting with the “run” (difference of the ![]() -coordinates):
-coordinates):
(1) 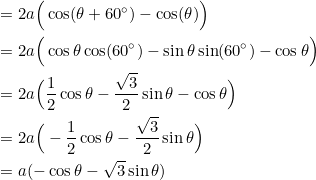
Next, we calculate the “rise” of side ![]() (difference of the
(difference of the ![]() -coordinates):
-coordinates):
(2) 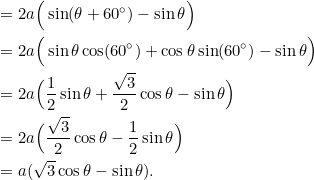
We can now calculate the length of side ![]() , using the last lines in (1) and (2):
, using the last lines in (1) and (2):
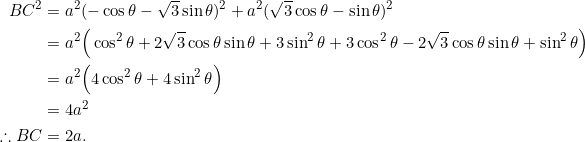
Since ![]() , the given coordinates yield an equilateral triangle of length
, the given coordinates yield an equilateral triangle of length ![]() . Conversely, to see that every equilateral triangle can be described this way, CLICK HERE.
. Conversely, to see that every equilateral triangle can be described this way, CLICK HERE.
Example 2
Find coordinates for the vertices of an equilateral triangle ![]() of length
of length ![]() where one side is parallel to the
where one side is parallel to the ![]() -axis, and one vertex is at the origin
-axis, and one vertex is at the origin ![]() .
.
This is the traditional case in which ![]() . Since we’re also given
. Since we’re also given ![]() , the two other vertices are
, the two other vertices are
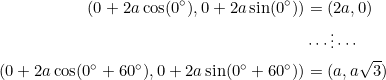
The vertices are ![]() .
.
Notice that the slopes of sides ![]() are
are ![]() , respectively. They form an arithmetic progression with a common difference of
, respectively. They form an arithmetic progression with a common difference of ![]() (or a common difference of
(or a common difference of ![]() , if we reverse the numbers). So this particular equilateral triangle comes equipped, naturally, with slopes in arithmetic progression.
, if we reverse the numbers). So this particular equilateral triangle comes equipped, naturally, with slopes in arithmetic progression.
In an equilateral triangle, SUM OF PRODUCT OF SLOPES, taken two slopes at a time=-3: CLICK HERE for a sample.
We’ll prove this in Example 7, but for now notice that ![]() .
.
Example 3
Find coordinates for the vertices of an equilateral triangle ![]() of length
of length ![]() in which one vertex is at
in which one vertex is at ![]() , and side
, and side ![]() makes an angle of
makes an angle of ![]() with the positive
with the positive ![]() -axis.
-axis.
Using ![]() and
and ![]() in Example 1, we obtain the two other vertices’ coordinates:
in Example 1, we obtain the two other vertices’ coordinates:
![Rendered by QuickLaTeX.com \begin{equation*} \begin{split} \Big(0+4a\cos(45^{\circ}),0+4a\sin(45^{\circ})\Big)&=(2a\sqrt{2},2a\sqrt{2})\\ &\cdots\vdots\cdots\\ \Big(0+4a[\cos(45^{\circ}+60^{\circ})],0+4a[\sin(45^{\circ}+60^{\circ})]\Big)&=(x,y)\\ x&=a\sqrt{2}(1-\sqrt{3})\\ y&=a\sqrt{2}(1+\sqrt{3}). \end{split} \end{equation}](https://blog.fridaymath.com/wp-content/ql-cache/quicklatex.com-54031d9b3f70f552d8e2833799641696_l3.png)
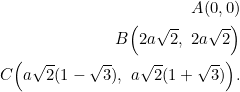
We can use these vertices to calculate the slopes of the sides:

Since ![]() , these slopes form a geometric progression with a common ratio of
, these slopes form a geometric progression with a common ratio of ![]() , depending on how we arrange the numbers. So, this particular equilateral triangle comes equipped, naturally, with slopes in geometric progression.
, depending on how we arrange the numbers. So, this particular equilateral triangle comes equipped, naturally, with slopes in geometric progression.
It follows that by changing the inclination angle of the base, the sequences formed by the slopes also change. Therefore, the traditional case (having one vertex at ![]() and one side parallel to the
and one side parallel to the ![]() -axis) is inadequate for what we want to investigate, which then necessitates the alternate — and “ultimate” — coordinates, given in Example 1.
-axis) is inadequate for what we want to investigate, which then necessitates the alternate — and “ultimate” — coordinates, given in Example 1.
Slopes of equilateral triangles
If we’re given a set of three numbers for the slopes of the sides of a triangle, we can easily tell if the triangle is equilateral.
Example 4
PROVE that any triangle whose sides have slopes ![]() is equilateral.
is equilateral.
Imagine a ![]() in which sides
in which sides ![]() have slopes
have slopes ![]() as shown below:
as shown below:
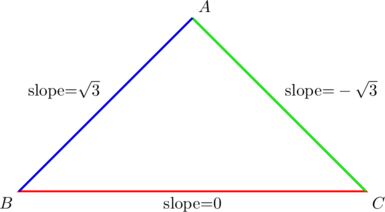
Using the fact that the acute angle ![]() between two lines with slopes
between two lines with slopes ![]() and
and ![]() can be given by
can be given by ![]() , we have:
, we have:
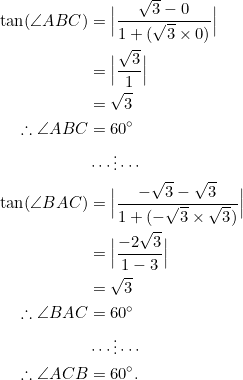
Since each interior angle of ![]() measures
measures ![]() , we conclude that this triangle is equilateral. (Compare Example 4 with Example 2.)
, we conclude that this triangle is equilateral. (Compare Example 4 with Example 2.)
Example 5
PROVE that any triangle whose sides have slopes ![]() is equilateral.
is equilateral.
As in the previous example, suppose that a certain ![]() has sides
has sides ![]() with slopes
with slopes ![]() as shown:
as shown:
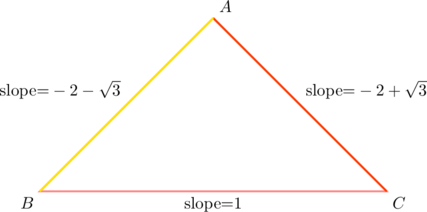
Then:
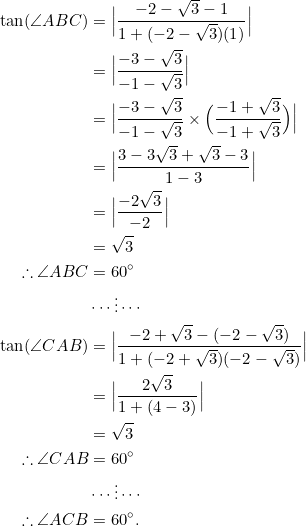
Compare Example 5 with Example 3.
Characterizing slopes of equilateral triangles
Due to the result below, we can always assume that the slopes of the sides of any equilateral triangle are of the form ![]() .
.
Example 6
Let ![]() be a triangle. PROVE that the following are equivalent:
be a triangle. PROVE that the following are equivalent:
 is equilateral;
is equilateral;- the slopes of its sides are
 .
.
What happens when the denominators are zero, namely when ![]() ? Easy. The orientation of the resulting equilateral triangle reduces to the “basic” case where one side is parallel to the
? Easy. The orientation of the resulting equilateral triangle reduces to the “basic” case where one side is parallel to the ![]() -axis. So there’s no issue with this — simply exclude it.
-axis. So there’s no issue with this — simply exclude it.
Now to the proof. First suppose that ![]() is equilateral with length
is equilateral with length ![]() . From Example 1 we know that its coordinates can be located at
. From Example 1 we know that its coordinates can be located at
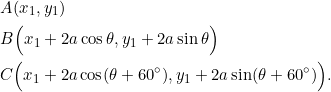
Using these coordinates, we can easily calculate the slopes of the sides:
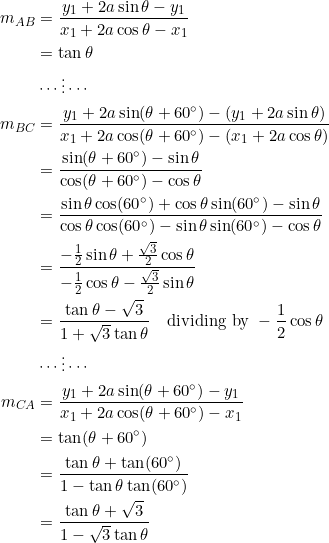
Conversely, suppose that the sides ![]() of
of ![]() have slopes of the form
have slopes of the form ![]() . Then, following similar calculations as in Example 4 and Example 5, we have, for example, that
. Then, following similar calculations as in Example 4 and Example 5, we have, for example, that ![]() :
:
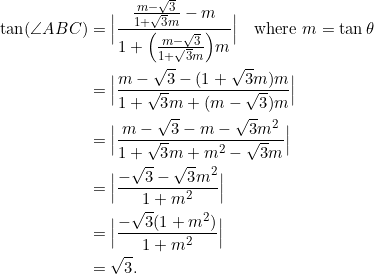
Example 7
In any equilateral triangle, PROVE that the sum of products of slopes, taken two slopes at a time, is always ![]() .
.
In view of Example 6, we can let the slopes of the sides be ![]() , and
, and ![]() . Then, taking two slopes at a time:
. Then, taking two slopes at a time:

Don’t forget to exclude ![]() .
.
Example 8
Let ![]() represent the slopes of an equilateral triangle. PROVE that
represent the slopes of an equilateral triangle. PROVE that ![]() . In other words, we have: sum of slopes is
. In other words, we have: sum of slopes is ![]() times product of slopes .
times product of slopes .
We characterized the slopes of equilateral triangles in Example 6, so let’s utilize that characterization. The slopes will be ![]() , and
, and ![]() .
.
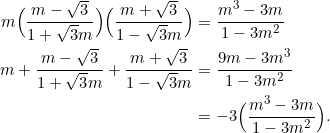
Example 9
PROVE that the slopes of the sides of an equilateral triangle cannot ALL be positive .
Let the slopes be ![]() . From Example 8 above, we have that
. From Example 8 above, we have that ![]() . So, the slopes cannot all be positive — otherwise both the sum
. So, the slopes cannot all be positive — otherwise both the sum ![]() and the product
and the product ![]() will be positive, making it impossible to have
will be positive, making it impossible to have ![]() .
.
Example 10
Let ![]() . PROVE that the slopes
. PROVE that the slopes ![]() form a geometric progression.
form a geometric progression.
Let’s use the fact that three numbers ![]() form a geometric progression precisely when
form a geometric progression precisely when ![]() . Then:
. Then:
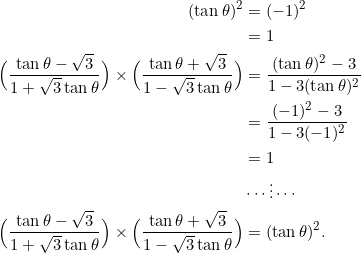
Takeaway
We’ve seen that equilateral triangles are naturally equipped with slopes in arithmetic and geometric progressions — depending on the “base inclination”. Interestingly, it turns out that every triangle contains a “sub-triangle” whose slopes form a geometric progression or an arithmetic progression. We’ll show you how this works in some subsequent posts.
Tasks
- PROVE that the slopes of the sides of an equilateral triangle cannot all be negative.
- Let
 be the slopes of the sides of a triangle. PROVE that the following conditions are equivalent:
be the slopes of the sides of a triangle. PROVE that the following conditions are equivalent:
- the triangle is equilateral;
- both
 and
and  hold.
hold.
- In an equilateral
 , assume that the slopes of the sides
, assume that the slopes of the sides  are
are  (all non-zero), and that the slopes of the medians from
(all non-zero), and that the slopes of the medians from  are
are  , respectively. PROVE that:
, respectively. PROVE that:
 ;
;- if
 form a geometric progression, then so do the median slopes
form a geometric progression, then so do the median slopes  .
.
- (Unique quadratic) Suppose that the slopes of the sides of an equilateral triangle form a geometric sequence with common ratio
 . Then, in view of the previous exercise, the slopes of the three medians also form a geometric sequence; let its common ratio be
. Then, in view of the previous exercise, the slopes of the three medians also form a geometric sequence; let its common ratio be  . PROVE that:
. PROVE that:


- Hence, deduce that both
 and
and  satisfy the quadratic equation
satisfy the quadratic equation  . (The two solutions of this quadratic equation are the only admissible values for the common ratio, should the slopes of the sides — and medians — of an equilateral triangle form geometric progressions.)
. (The two solutions of this quadratic equation are the only admissible values for the common ratio, should the slopes of the sides — and medians — of an equilateral triangle form geometric progressions.)
- (Three nil) For an equilateral triangle
 with side slopes
with side slopes  in geometric progression and median slopes
in geometric progression and median slopes  (also in geometric progression, in view of a previous exercise), PROVE that:
(also in geometric progression, in view of a previous exercise), PROVE that:
 ;
; ;
; .
.
- (“Cancellation” property) If the slopes of the sides of an equilateral triangle
 form a geometric progression and
form a geometric progression and  , PROVE that
, PROVE that  also (thus appearing to “cancel” out
also (thus appearing to “cancel” out  ).
).
(We might be able to do some group theory here. )
) - PROVE that the slopes of the sides of an equilateral triangle form an arithmetic progression if, and only if, one of the slopes is
 .
. - (“Cancellation” property) If the slopes of the sides of an equilateral triangle
 form an arithmetic progression and
form an arithmetic progression and  , PROVE that
, PROVE that  also (thus appearing to “cancel” out
also (thus appearing to “cancel” out  ).
). - Under what condition(s) can the sum of the slopes of an equilateral triangle be equal to the product of the slopes?
- (Unique sum) Let
 be the slopes of the sides of an equilateral triangle. PROVE that
be the slopes of the sides of an equilateral triangle. PROVE that  form a geometric progression if, and only if,
form a geometric progression if, and only if, 