Easy condition for perpendicular medians

With us in the crew today are two perpendicular medians, who have something new to say. It’s possible you already knew what they’ll say, but let’s continue all the same. Or, you can jump straight to Example 8.

Join us to welcome perpendicular medians, chief host of today’s post!!!

Median lengths in terms of side lengths

Let $\triangle ABC$ be a triangle whose side lengths are $a,b,c$ . Throughout we’ll adopt the usual convention of denoting the lengths of the medians from vertices $A,B,C$ by $m_{a},m_{b},m_{c}$ , respectively.

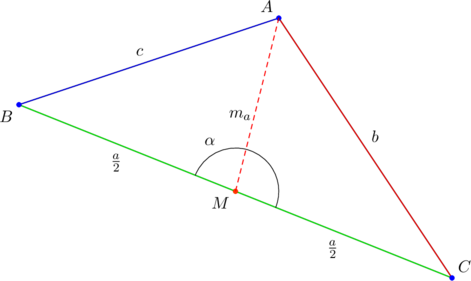
In the above diagram, the median $AM$ has length $m_{a}$ . Also, $\angle AMB=\alpha$ , and so $\angle AMC=180^{\circ}-\alpha.$ Notice the side lengths of the triangle as indicated.

Example 1

PROVE that $m^2_{a}=\frac{2b^2+2c^2-a^2}{4},~m^2_{b}=\frac{2a^2+2c^2-b^2}{4},$ and $m^2_{c}=\frac{2a^2+2b^2-c^2}{4}.$

We only prove the first one, as the other two follow similarly (or by “symmetry”). Let’s use the cosine law to this end.

Applied to $\triangle ABM$ , the cosine law gives, for side $AB$ :

$\begin{equation*} \begin{split} AB^2&=AM^2+MB^2-2\times AM\times MB\times \cos(\angle AMB)\\ c^2&=m_{a}^2+\Big(\frac{a}{2}\Big)^2-2\times m_{a}\times \Big(\frac{a}{2}\Big)\times\cos(\alpha)\\ c^2&=m_{a}^2+\frac{a^2}{4}-am_{a}\cos(\alpha) \end{split} \end{equation}$

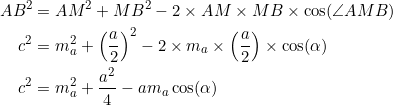
Similarly, the cosine law applied to $\triangle AMC$ gives, for side $AC$ :

$\begin{equation*} \begin{split} AC^2&=AM^2+MC^2-2\times AM\times MC\times\cos(\angle AMC)\\ b^2&=m_{a}^2+\Big(\frac{a}{2}\Big)^2-2\times m_{a}\times\Big(\frac{a}{2}\Big)\times\cos(180^{\circ}-\alpha)\\ b^2&=m_{a}^2+\frac{a^2}{4}-am_{a}\cos(180^{\circ}-\alpha)\\ b^2&=m_{a}^2+\frac{a^2}{4}+am_{a}\cos(\alpha)\\ \end{split} \end{equation}$

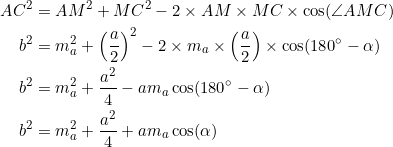
In the last step we used the trigonometric identity $\cos(180^{\circ}-\alpha)=-\cos(\alpha)$ . So we’ve got two equations:

(1) $\begin{equation*} c^2&=m_{a}^2+\frac{a^2}{4}-am_{a}\cos(\alpha). \end{equation*}$

(2) $\begin{equation*} b^2&=m_{a}^2+\frac{a^2}{4}+am_{a}\cos(\alpha). \end{equation*}$

Adding (1) and (2), the term involving $am_{a}\cos(\alpha)$ gets eliminated, leaving behind

$b^2+c^2=2m_{a}^2+\frac{2a^2}{4},$

which can be re-arranged to give $m^2_{a}=\frac{2b^2+2c^2-a^2}{4},$ as desired.

Example 2

PROVE that $m^2_{a}+m^2_{b}+m^2_{c}=\frac{3}{4}(a^2+b^2+c^2).$

We simply use the expressions from Example 1: $m^2_{a}+m^2_{b}+m^2_{c}$

$\begin{equation*} \begin{split} &=\Big(\frac{2b^2+2c^2-a^2}{4}\Big)+\Big(\frac{2a^2+2c^2-b^2}{4}\Big)+\Big(\frac{2a^2+2b^2-c^2}{4}\Big)\\ &=\frac{3}{4}\Big(a^2+b^2+c^2\Big). \end{split} \end{equation}$

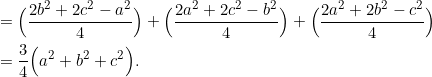
For our purposes, the above relationship is very vital.

Example 3

PROVE that $m_{a}^2-m_{b}^2=\frac{3}{4}(b^2-a^2).$

Again, we use the expressions from Example 1:

$\begin{equation*} \begin{split} m_{a}^2-m_{b}^2&=\Big(\frac{2b^2+2c^2-a^2}{4}\Big)-\Big(\frac{2a^2+2c^2-b^2}{4}\Big)\\ &=\frac{3}{4}\Big(b^2-a^2\Big). \end{split} \end{equation}$

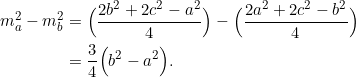
Example 4

PROVE that in any triangle, the longer sides have shorter medians.

We use the result of Example 3 above. Suppose that in $\triangle ABC$ we have $b>a$ . Since

$m_{a}^2-m_{b}^2=\frac{3}{4}(b^2-a^2),$

the right side is positive. The left side must be positive as well, so $m_{a}^2>m_{b}^2$ . Since median lengths are positive quantities, we can extract square roots to obtain $m_{a}>m_{b}$ .

If then there’s an ordering $c>b>a$ , it will follow that $m_{a}>m_{b}>m_{c}$ , using the transitivity property of inequalities.

Example 5

Find coordinates for the vertices of a $\triangle ABC$ that has the following property: $m_{a}=a.$

If all we needed were the side lengths, then we could use the equation $m_{a}=a$ and the fact that $m^2_{a}=\frac{2b^2+2c^2-a^2}{4}$ to obtain the relation $5a^2=2b^2+2c^2$ and thereby find suitable side lengths.

We’ll instead appeal to triangles whose slopes are in geometric progression, as these provide us with a ready-made solution. Consider $\triangle ABC$ below, with vertices at $A(1,9),~B(0,0),~C(-2,6)$ :

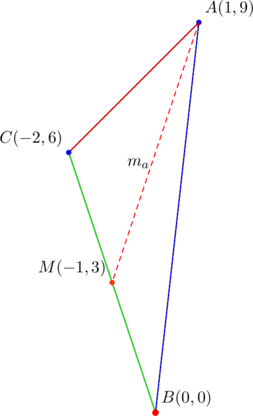
Using the given coordinates, we find, by the distance formula, that:

$\begin{equation*} \begin{split} AM^2&=(1--1)^2+(9-3)^2\\ &=40\\ AM&=\sqrt{40}\\ &=2\sqrt{10}\\ \therefore m_{a}&=2\sqrt{10}\quad\textrm{(\textbf{in view of the diagram})}\\ BC^2&=(-2-0)^2+(6-0)^2\\ &=40\\ BC&=\sqrt{40}\\ &=2\sqrt{10}\\ \therefore a&=2\sqrt{10}\quad\textrm{(\textbf{since BC=a, by usual notation})}. \end{split} \end{equation}$

So we obtain for the above triangle,whose vertices are $A(1,9),~B(0,0),~C(-2,6)$ , that $m_{a}=a$ .

Notice that the slopes of the sides of $\triangle ABC$ given above are $1,-3,9$ ; so they form a geometric progression with a common ratio of $-3$ . There’s something quite interesting that’s hidden there: in any triangle whose sides slopes form a geometric progression with a common ratio of $-3$ , there is a vertex $A$ such that $m_{a}=a$ .

Conditions for perpendicular medians

Example 6

PROVE that medians from vertex $A$ and vertex $B$ are perpendicular if, and only if, $a^2+b^2=5c^2$ .

First suppose that the median $AM$ through vertex $A$ and the median $BN$ through vertex $B$ are perpendicular. Consider the diagram below, where $G$ is the centroid of $\triangle ABC$ :

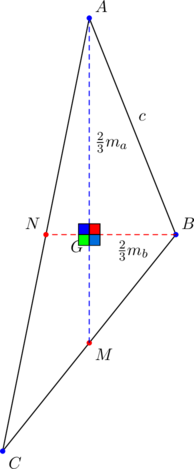
Since the centroid divides the median in the ratio $2:1$ , we have, in $\triangle AGB$ , that $AG=\frac{2}{3}m_{a}$ and $GB=\frac{2}{3}m_{b}$ . By assumption, $\triangle AGB$ is a right triangle, so the Pythagorean theorem applied to it gives:

$\begin{equation*} \begin{split} AB^2&=AG^2+GB^2\\ c^2&=\Big(\frac{2}{3}m_{a}\Big)^2+\Big(\frac{2}{3}m_{b}\Big)^2\\ c^2&=\frac{4}{9}(m_{a}^2+m_{b}^2)\\ c^2&=\frac{4}{9}\Big(\frac{2b^2+2c^2-a^2}{4}+\frac{2a^2+2c^2-b^2}{4}\Big)\\ c^2&=\frac{4}{9}\Big(\frac{a^2+b^2+4c^2}{4}\Big)\\ 9c^2&=a^2+b^2+4c^2\\ 5c^2&=a^2+b^2. \end{split} \end{equation}$

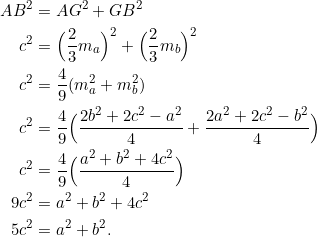
Conversely, if we suppose that the relation $a^2+b^2=5c^2$ holds, then we need to show that $\angle AGB=90^{\circ}$ . We’ll use the cosine rule to this end.

$\begin{equation*} \begin{split} \cos(\angle AGB)&=\frac{AG^2+GB^2-AB^2}{2\times AG\times GB}\\ &=\frac{\Big(\frac{2}{3}m_{a}\Big)^2+\Big(\frac{2}{3}m_{b}\Big)^2-c^2}{2\times \frac{2}{3}m_{a}\times\frac{2}{3}m_{b} }\\ &=\frac{\frac{4}{9}(m_{a}^2+m_{b}^2)-c^2}{\frac{8}{9}m_{a}m_{b}}\\ &=\frac{\frac{4}{9}\Big(\frac{2b^2+2c^2-a^2}{4}+\frac{2a^2+2c^2-b^2}{4}\Big)-c^2}{\frac{8}{9}m_{a}m_{b}}\\ &=\frac{\frac{4}{9}\Big(\frac{a^2+b^2+4c^2}{4}\Big)-c^2}{\frac{8}{9}m_{a}m_{b}}\\ &=\frac{\frac{4}{9}\Big(\frac{5c^2+4c^2}{4}\Big)-c^2}{\frac{8}{9}m_{a}m_{b}}\\ &=0\\ \angle AGB&=90^{\circ}. \end{split} \end{equation}$

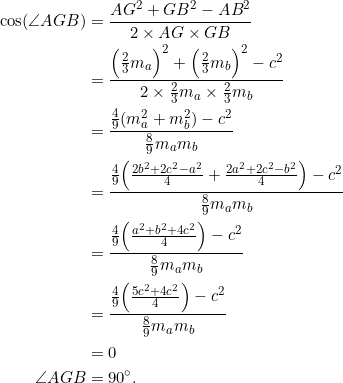
This shows that the medians are perpendicular.

Example 7

PROVE that $a^2+b^2=5c^2$ if, and only if, $m^2_{a}+m^2_{b}=m^2_{c}$ .

We first prove: $a^2+b^2=5c^2\implies m^2_{a}+m^2_{b}=m^2_{c}$ .

$\begin{equation*} \begin{split} m^2_{a}+m^2_{b}&=\Big(\frac{2b^2+2c^2-a^2}{4}\Big)+\Big(\frac{2a^2+2c^2-b^2}{4}\Big)\\ &=\frac{a^2+b^2+4c^2}{4}\\ &=\frac{5c^2+4c^2}{4}\\ &=\frac{9c^2}{4}\\ m_{c}^2&=\frac{2a^2+2b^2-c^2}{4}\\ &=\frac{2(a^2+b^2)-c^2}{4}\\ &=\frac{2(5c^2)-c^2}{4}\\ &=\frac{9c^2}{4}\\ &=m^2_{a}+m^2_{b}. \end{split} \end{equation}$

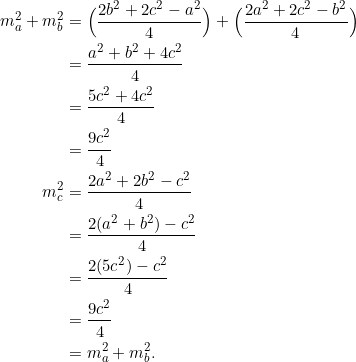
Next, let’s prove $m^2_{a}+m^2_{b}=m^2_{c}\implies a^2+b^2=5c^2$ .

$\begin{equation*} \begin{split} \frac{2b^2+2c^2-a^2}{4}+\frac{2a^2+2c^2-b^2}{4}&=\frac{2a^2+2b^2-c^2}{4}\\ a^2+b^2+4c^2&=2a^2+2b^2-c^2\\ 5c^2&=a^2+b^2. \end{split} \end{equation}$

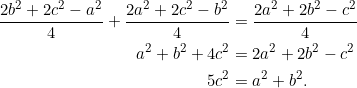
If all math proofs were this simple!

An easier, equivalent condition

What we’ve featured in our next example is somewhat absent in literature because it’s so miniature. Put differently, it is not found because it is not profound. But it still counts!

Example 8

PROVE that $a^2+b^2=5c^2$ if, and only if, $m_{c}=\frac{3}{2}c$ .

As you can see, this is extremely easy. To obtain the implication $a^2+b^2=5c^2\implies m_{c}=\frac{3}{2}c$ , begin with the expression for $m_{c}^2$ :

$\begin{equation*} \begin{split} m_{c}^2&=\frac{2a^2+2b^2-c^2}{4}\\ &=\frac{2(a^2+b^2)-c^2}{4}\\ &=\frac{2(5c^2)-c^2}{4}\\ &=\frac{9c^2}{4}\\ \therefore m_{c}&=\frac{3}{2}c. \end{split} \end{equation}$

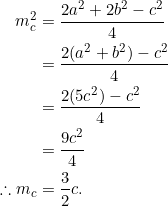
Conversely, if $m_{c}=\frac{3}{2}c$ , then $m_{c}^2=\frac{9}{4}c^2$ . So using the expression for $m_{c}^2$ again, we have:

$\begin{equation*} \begin{split} \frac{2a^2+2b^2-c^2}{4}&=\frac{9}{4}c^2\\ 2a^2+2b^2-c^2&=9c^2\\ 2a^2+2b^2&=10c^2\\ a^2+b^2&=5c^2. \end{split} \end{equation}$

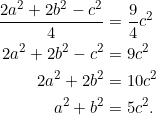
Example 9

For any $\triangle ABC$ with the usual notation, PROVE that each of the following statements implies the others:

median through vertex $A$ and median through vertex $B$ are perpendicular;
$a^2+b^2=5c^2$ ;
$m^2_{a}+m^2_{b}=m^2_{c}$ ;
$m_c=\frac{3}{2}c.$

Actually, this has been done in Example 6, Example 7, and Example 8; we just collect and connect them together here.

Notice that $(1)\iff(2)$ by virtue of Example 6. Also, $(2)\iff(3)$ is due to Example 7. Then, Example 8 verifies that $(2)\iff(4)$ .

(As a result, we obtain $(1)\iff(3)$ , $(1)\iff(4)$ , and $(3)\iff(4)$ . Each statement therefore implies the others.)

Example 10

Find coordinates for the vertices of a triangle that contains two perpendicular medians.

The easiest way to do this is to start with any three “consecutive” numbers, let’s say $1,2,3$ . Then, form three pairs as follows: $(1,2),(2,1),(3,3)$ . That’s it!!! Though with a little caveat: the order is important. You won’t get a triangle with something like $(1,1),(2,2),(3,3)$ .

To get a “bigger” triangle, we can space out the numbers, like so: $1,4,7$ , then use the three pairs $(1,4),(4,1),(7,7)$ as our triangle’s vertices, as shown below:

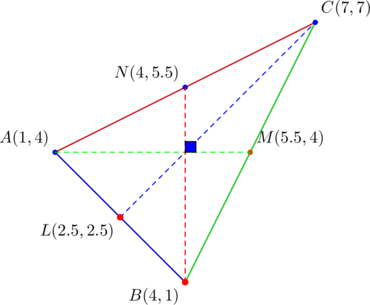
Notice the horizontal median $AM$ and the vertical median $BN$ . So these medians are perpendicular. With the given coordinates and the usual notation, let’s write out the three other equivalent conditions:

$\begin{equation*} \begin{split} a^2&=(7-4)^2+(7-1)^2\\ \therefore a^2&=45\\ b^2&=(7-1)^2+(7-4)^2\\ \therefore b^2&=45\\ c^2&=(1-4)^2+(4-1)^2\\ \therefore c^2&=18\\ &\cdots\vdots\cdots\\ a^2+b^2&=45+45\\ \therefore a^2+b^2&=90\\ 5c^2&=5\times 18=90\\ \therefore 5c^2&=a^2+b^2\\ &\cdots\vdots\cdots\\ m_{a}^2&=(1-5.5)^2+(4-4)^2\\ \therefore m_{a}^2&=20.25\\ m_{b}^2&=(4-4)^2+(1-5.5)^2\\ \therefore m_{b}^2&=20.25\\ m_{c}^2&=(7-2.5)^2+(7-2.5)^2\\ \therefore m_{}^2&=40.50\\ &\cdots\vdots\cdots\\ m_{a}^2+m_{b}^2&=20.25+20.25\\ &=40.50\\ \therefore m_{a}^2+m_{b}^2&=m_{c}^2\\ &\cdots\vdots\cdots\\ \textrm{Using}~m_{c}^2&=40.50\\ \textrm{We obtain}~m_{c}&=\sqrt{40.50}\\ &=4.5\sqrt{2}\\ \textrm{Using}~c^2&=18\\ \textrm{We obtain}~c&=\sqrt{18}\\ &=3\sqrt{2}\\ \therefore m_{c}&=\frac{3}{2}c. \end{split} \end{equation}$

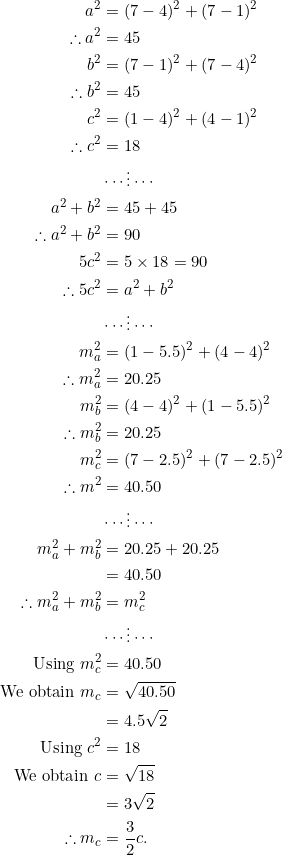
In providing examples of perpendicular medians using coordinates, it is always convenient to use the special case in which one median is vertical and the other horizontal. But there are other cases in which the (two perpendicular) medians are neither vertical nor horizontal — for example, the triangle with vertices at $A(-2,\frac{1}{3}),B(-3,-4),C(4,-\frac{1}{3})$ is such. It may happen that we devote another post to those.

Takeaway

Of all the three other equivalent conditions for perpendicular medians, it is clear that $m_c=\frac{3}{2}c$ is the simplest in “appearance”, but maybe not in application — particularly because it uses the length of one of the medians, so one cannot tell immediately based on the side lengths.

If all the side lengths $a,b,c$ are provided, always use $a^2+b^2=5c^2$ in checking for perpendicular medians (assuming you’re concerned with the medians through vertices $A$ and $B$ ), but be aware of its equivalent formulations.

Lastly, to every triangle is a median triangle, whose side lengths are the lengths of the medians of the original triangle. Thus, the median triangle is a right triangle if, and only if, the original triangle contains two perpendicular medians.

Tasks

Suppose that $\triangle ABC$ is such that $m_{a}=\frac{\sqrt{3}}{2}a$ and $m_{b}=\frac{\sqrt{3}}{2}b$ . PROVE that the triangle is equilateral.
$\Big($ As shown in the next exercise, having $m_{a}=\frac{\sqrt{3}}{2}a$ alone is not enough to make a triangle equilateral. Also, observe that both $m_{a}=\frac{\sqrt{3}}{2}a$ and $m_{b}=\frac{\sqrt{3}}{2}b$ together imply that $m_{c}=\frac{\sqrt{3}}{2}c$ , so requiring all three conditions is asking for too much. $\Big)$
(This exercise shows that it is possible to have a median whose length is of the form $m_{a}=\frac{\sqrt{3}}{2}a$ , even when the triangle is not equilateral.) To this end, let , , and be the vertices of . PROVE that:
- $m_{a}^2=\frac{3}{4}a^2$
- $m_{b}^2=\frac{21}{4}b^2$
- $m_{c}^2=\frac{3}{4}b^2$
- $m_{c}^2=\frac{3}{28}c^2$
- $b^2+c^2=2a^2$
- $m_{b}^2+m_{c}^2=2m_{a}^2$
- the slopes of sides $AC,CB,BA$ form a geometric progression whose common ratio is $-2-\sqrt{3}.$
(Nice Nine)For any triangle with the usual notation, PROVE that the following NINE statements are equivalent:
- $m^2_{a}=\frac{3}{4}a^2;$
- $m^2_{b}=\frac{3}{4}c^2;$
- $m^2_{c}=\frac{3}{4}b^2;$
- $b^2+c^2=2a^2$ ;
- $m_{b}^2+m_{c}^2=2m_{a}^2$ ;
- $m^2_{a}+m^2_{b}=\frac{3}{4}(a^2+c^2)$ ;
- $m^2_{a}+m^2_{c}=\frac{3}{4}(a^2+b^2)$ ;
- $m^2_{b}+m^2_{c}=\frac{3}{2}a^2$ ;
- $m^2_{a}+m^2_{c}+m^2_{c}=\frac{9}{4}a^2$ .
Suppose that the side lengths $a,b,c$ of a $\triangle ABC$ are related via $c^2=k(a^2+b^2)$ . PROVE that $0< k < 2$ .
$\Big($ More generally, we can find constants $k_{1},k_{2},k_{3}$ such that $c^2=k_{1}(a^2+b^2),~b^2=k_{2}(a^2+c^2),~a^2=k_{3}(b^2+c^2)$ , and $0< k_{1}< 2,~0< k_{2}< 2, ~0< k_{3}< 2$ . $\Big)$
PROVE that there is no $\triangle ABC$ in which the side lengths $a,b,c$ satisfy $c^2=2(a^2+b^2)$ .
$\Big($ Just to buttress the point that the strict inequality in the preceding exercise is crucial. Simply calculate the length $m_{c}$ of the median from vertex $C$ to see why the claim is valid. $\Big)$
Let be such that the side lengths are related via . PROVE that:
- $\triangle ABC$ is either scalene or else equilateral;
- $m_{c}>m_{a}>m_{b}$ or $m_{b}>m_{a}>m_{c}$ (both for the scalene case);
- $\frac{1}{2}<\cos A<1$ (and so $0^{\circ}< A<60^{\circ}$ , for the scalene case).
Let $k$ be a positive constant. PROVE that $m_{c}=kc$ if, and only if, $(4k^2+1)c^2=2a^2+2b^2$ .
$\Big($ In particular, if $k=\frac{1}{2}$ , we obtain $m_{c}=\frac{1}{2}c\iff c^2=a^2+b^2$ , which expresses the popular fact that the length of the median to the hypotenuse of a right triangle is half the length of the hypotenuse. And, only right triangles have this property. $\Big)$
Suppose that $m_{c}=kc$ for some constant $k$ . What are the admissible values of $k$ ?
PROVE that $m_{a}^2+2m_{b}^2+3m_{c}^2=\frac{3}{4}\Big(3a^2+2b^2+c^2\Big)$ and that $m_a}^2+2m_{b}^2-3m_{c}^2=\frac{3}{4}\Big(3c^2-2b^2-a^2\Big)$ .
PROVE that the three medians in a right triangle satisfy $m_{a}^2+m_{b}^2=5m_{c}^2$ , where $c$ is the length of the hypotenuse.
PROVE that $m_{a}\geq \frac{(b+c)\sin B\sin C}{\sin B+\sin C}$ .
PROVE that $m_{a}=\frac{\sqrt{a^2+2bc}}{2}$ if, and only if, $\angle A=60^{\circ}$ .
PROVE that an equilateral triangle can never contain two perpendicular medians.
(Not everything goes the way of equilateral triangles after all.)
PROVE that the medians to the “two legs” in a right triangle can never be perpendicular.