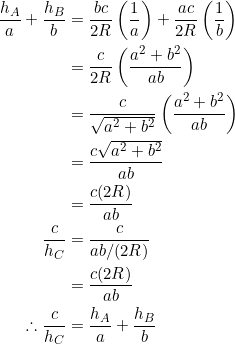(1) ![]()
Unsurprisingly, such triangles mirror many of the properties of right triangles, with minor differences. So, for the time being, we’re giving them the pseudonym pseudo right triangles.
In our calculations we’ll frequently utilize the fact that equation (1) is equivalent to
(2) ![]()
where ![]() is the circumradius of the parent triangle
is the circumradius of the parent triangle ![]() .
.
Identities
A random selection of simple properties, in addition to the ones we already explored before and maybe in preparation for subsequent discussions.
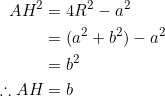
Once one has ![]() , one also has
, one also has ![]() automatically. They imply each other. Symbolically,
automatically. They imply each other. Symbolically, ![]() .
.
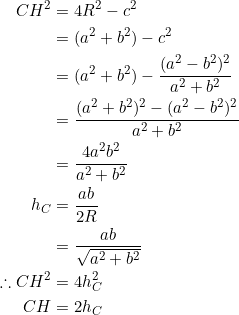
For a right triangle this would be ![]() , if
, if ![]() . In general, where a right triangle has a “degenerate” property, a triangle satisfying equation (1) doesn’t seem to. A case in point is the orthic triangle.
. In general, where a right triangle has a “degenerate” property, a triangle satisfying equation (1) doesn’t seem to. A case in point is the orthic triangle.
This follows from example 2 above, because we had ![]() , together with the fact that
, together with the fact that ![]() is the length of the altitude from
is the length of the altitude from ![]() . In other words, the distance from
. In other words, the distance from ![]() to the foot of the altitude from
to the foot of the altitude from ![]() is equal to the distance from the foot of this altitude to the orthocenter.
is equal to the distance from the foot of this altitude to the orthocenter.
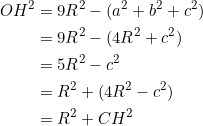
So we can form a right triangle with hypotenuse equal to the Euler segment ![]() having
having ![]() and
and ![]() as legs.
as legs.
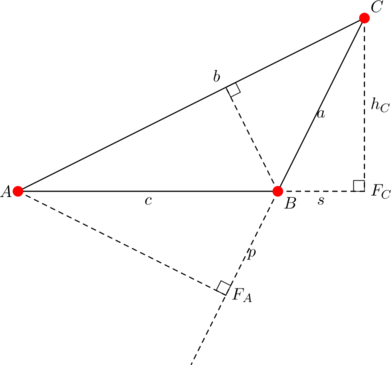
Using the fact that ![]() and the Pythagorean theorem
and the Pythagorean theorem
![]()
gives ![]() , as desired. Next, multiply both sides by
, as desired. Next, multiply both sides by ![]() and use the fact that
and use the fact that ![]() from our previous post:
from our previous post:
![]()
Inequalities
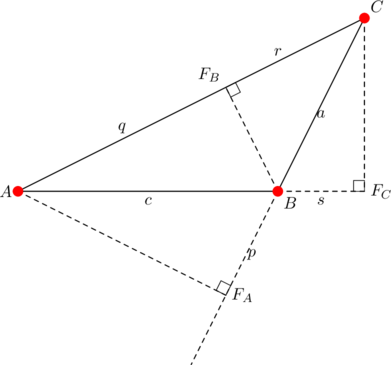
In our previous post we had ![]() . Re-arrange as
. Re-arrange as ![]() . Then
. Then
![]()
We also had ![]() in our last post, so
in our last post, so ![]() too.
too.
Inverses
Two “upside-down” Pythagorean identities.
Equation (1) says that ![]() . Now, if
. Now, if ![]() is the golden ratio, then
is the golden ratio, then ![]() .
.
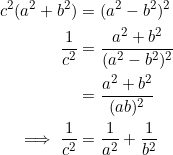
(Also happens in a Kepler triangle ![]() .)
.)

In example 5 we had ![]() , so (assuming
, so (assuming ![]() ) we have
) we have
![]()
Re-arrange:
![]()
This would also imply ![]() . And so
. And so ![]() is the geometric mean of
is the geometric mean of ![]() and
and ![]() , while
, while ![]() is the geometric mean of
is the geometric mean of ![]() and
and ![]() .
.
Tasks
- (Keeping track) Let
 be the side-lengths of an obtuse triangle
be the side-lengths of an obtuse triangle  ,
,  its circumradius,
its circumradius,  its circumcenter,
its circumcenter,  its orthocenter, and
its orthocenter, and  the altitudes. PROVE that each of the following statements implies the others:
the altitudes. PROVE that each of the following statements implies the others:















 or
or 

- the orthic triangle is isosceles
- the geometric mean theorem holds
- the bisector of
 has length
has length  , where
, where 
- the orthocenter is a reflection of vertex
 over side
over side 
( statements to help you remember 2021. Aside: the ratio of the length of the angle bisector of
statements to help you remember 2021. Aside: the ratio of the length of the angle bisector of  to the length of the altitude from vertex
to the length of the altitude from vertex  is
is  , under the above equivalence.)
, under the above equivalence.)
- (Kepler triangle) Suppose that
 satisfies the usual Pythagorean identity
satisfies the usual Pythagorean identity  . PROVE that the following four statements are equivalent:
. PROVE that the following four statements are equivalent:
-
 form a geometric progression
form a geometric progression  is the golden ratio
is the golden ratio-

 .
.
-
- (Kosnita theorem) If
 satisfies equation (1), PROVE that the Kosnita point coincides with vertex
satisfies equation (1), PROVE that the Kosnita point coincides with vertex  . (Somewhat exciting property.)
. (Somewhat exciting property.) - PROVE that the two statements below are equivalent for a triangle
 :
:


(If these were added to the original statements in the first exercise, we will obtain a total of
statements in the first exercise, we will obtain a total of  . Cool. In terms of sheer numbers, we really wanted something that mirrors the Invertible Matrix Theorem. Reached.)
. Cool. In terms of sheer numbers, we really wanted something that mirrors the Invertible Matrix Theorem. Reached.)
- Consider
 with vertices at
with vertices at  ,
,  ,
,  . Its orthocenter is
. Its orthocenter is  , and its circumcenter is
, and its circumcenter is  .
.
- Verify that the foot of the altitude from vertex
 is
is  . Deduce that
. Deduce that  is the reflection of vertex
is the reflection of vertex  over side
over side  .
. - PROVE that the midpoint of
 together with
together with  form a parallelogram.
form a parallelogram.
(The midpoint of coincides with our favourite point
coincides with our favourite point  in this case.)
in this case.)
- Verify that the foot of the altitude from vertex