(1) ![]()
In addition, it has the property that its side-lengths form a geometric progression, for example:
(2) ![]()
Equations (1) and (2) force the ratio of the hypotenuse ![]() to one of the legs (
to one of the legs (![]() or
or ![]() ) to be golden:
) to be golden:
(3) ![]()
In this post, we show that a Kepler triangle also satisfies
(4) ![]()
which, in conjunction with equation (1), constitutes what one may call a double Pythagorean identity. We also show that if any of the four equations above hold, then the remaining three become equivalent.
For the Kepler triangle we have ![]() , where
, where ![]() is the golden ratio. By definition of
is the golden ratio. By definition of ![]() , we have
, we have ![]() and so
and so ![]() .
.
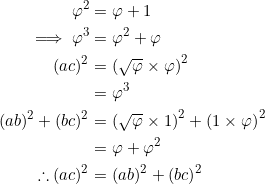
Note that a random right triangle need not satisfy equation (4). For example, the very familiar case with ![]() ,
, ![]() ,
, ![]() doesn’t.
doesn’t.
Simple characterizations
A couple of trivial equivalent statements that offer alternate descriptions of the Kepler triangle.
In other words, the following three statements are equivalent for any right triangle (in which ![]() ):
):
- the side-lengths form a geometric progression

- the ratio
 is the golden ratio
is the golden ratio - the identity
 holds.
holds.
The result follows if we show that ![]() .
.
So let’s suppose that ![]() holds, that is, the sequence
holds, that is, the sequence ![]() is geometric. This gives
is geometric. This gives ![]() . Since we also have that
. Since we also have that ![]() , it means that
, it means that
![]()
Thus, ![]() satisfies the defining equation for the golden ratio, and so
satisfies the defining equation for the golden ratio, and so ![]() holds.
holds.
Next, we show that ![]() . So suppose that
. So suppose that ![]() is the golden ratio. Then
is the golden ratio. Then
![]()
Multiply both sides of ![]() by
by ![]() to get
to get
![]()
since ![]() from the Pythagorean identity and also
from the Pythagorean identity and also ![]() from the golden ratio. Thus,
from the golden ratio. Thus, ![]() holds.
holds.
Finally, we show that ![]() . We have
. We have ![]() and
and ![]() :
:
![]()
So the sequence ![]() is geometric, and
is geometric, and ![]() is proved.
is proved.
Easy equivalence.
In other words, the following three statements are equivalent for any triangle in which ![]() :
:
- the triangle is a right triangle with

- the ratio
 is the golden ratio
is the golden ratio - the identity
 holds.
holds.
Follow the same argument as in example 2, bearing in mind that ![]() holds throughout in this case.
holds throughout in this case.
In other words, the following three statements are equivalent for any triangle in which ![]() :
:
- the triangle is a right triangle with

- the side-lengths form a geometric progression

- the identity
 holds.
holds.
Follow the same argument as in example 2, bearing in mind that ![]() holds throughout in this case.
holds throughout in this case.
In other words, the following three statements are equivalent for any triangle in which ![]() :
:
- the triangle is a right triangle with

- the side-lengths form a geometric progression

- the ratio
 is the golden ratio
is the golden ratio  .
.
Follow the same argument as in example 2, bearing in mind that ![]() holds throughout in this case.
holds throughout in this case.
Similar concept
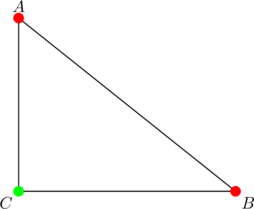
Given ![]() in which
in which ![]() , the Pythagorean theorem states that
, the Pythagorean theorem states that
(5) ![]()
(Or the usual ![]() .) But then the left side of equation (5) is just the sum of the squares of two altitudes — the altitude from vertex
.) But then the left side of equation (5) is just the sum of the squares of two altitudes — the altitude from vertex ![]() and the altitude from vertex
and the altitude from vertex ![]() — and so we can re-write (5) as:
— and so we can re-write (5) as:
(6) ![]()
where ![]() and
and ![]() are the altitudes from
are the altitudes from ![]() and
and ![]() . The latter equation expresses the fact that in a right triangle, the sum of the squares of two altitudes is equal to the square of the third side (the hypotenuse). We’ll use this intrinsic characteristic of right triangles as the defining condition for the triangles under consideration in the second part of today’s discussion.
. The latter equation expresses the fact that in a right triangle, the sum of the squares of two altitudes is equal to the square of the third side (the hypotenuse). We’ll use this intrinsic characteristic of right triangles as the defining condition for the triangles under consideration in the second part of today’s discussion.
First suppose that ![]() . Since
. Since ![]() and
and ![]() , we get
, we get
![]()
Conversely, suppose that ![]() . Then:
. Then:
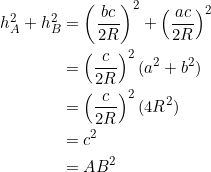
QED: ![]()
Begin with ![]() as per the extended law of sines. The rest is:
as per the extended law of sines. The rest is:
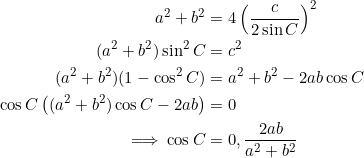
Since the given triangle is not a right triangle, we take ![]() from the preceding example. However, since
from the preceding example. However, since ![]() is always equal to
is always equal to ![]() in any triangle, we have:
in any triangle, we have:
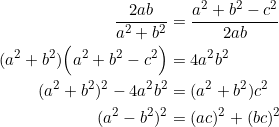
Similar to equation (4) for the Kepler triangle. Let’s take a shot at making it exact.
First suppose that ![]() . Since
. Since ![]() from the preceding example we must then have
from the preceding example we must then have ![]() . Positive square roots:
. Positive square roots: ![]() , or
, or ![]() , and so
, and so ![]() is the golden ratio. The converse is also easy. So basically, we have non-right triangles that tend to behave like the Kepler triangle.
is the golden ratio. The converse is also easy. So basically, we have non-right triangles that tend to behave like the Kepler triangle.
Special case
A sample triangle that satisfies equation (6) twice.
For this triangle we have:
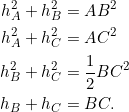
Takeaway
For any non-right triangle ![]() with side-lengths
with side-lengths ![]() , circumradius
, circumradius ![]() , and altitudes
, and altitudes ![]() , the five statements below are equivalent:
, the five statements below are equivalent:
In addition, if a non-right triangle satisfies any of the equivalent conditions above, then each of the following three statements implies the others:
 is the golden ratio
is the golden ratio
![Rendered by QuickLaTeX.com a,\sqrt[4]{5}c,b](//blog.fridaymath.com/wp-content/plugins/a3-lazy-load/assets/images/lazy_placeholder.gif) is a geometric sequence.
is a geometric sequence.
In a nutshell, we have a non-right triangle version of the Kepler triangle.
Tasks
- If a non-right triangle satisfies equation (6), PROVE that the length of the altitude from vertex
 can be given by
can be given by  .
. - Let
 be the side-lengths of a right triangle, where
be the side-lengths of a right triangle, where  is the hypotenuse, and let
is the hypotenuse, and let  be its circumradius. PROVE that:
be its circumradius. PROVE that:

 (in that order) cannot be a geometric sequence.
(in that order) cannot be a geometric sequence.
- PROVE: For any non-right triangle
 with side-lengths
with side-lengths  , circumradius
, circumradius  , and altitudes
, and altitudes  , the five statements below are equivalent:
, the five statements below are equivalent:
- Suppose that a non-right triangle satisfies any of the equivalent conditions in the preceding exercise. PROVE that:


 , where
, where  orthocenter,
orthocenter,  circumcenter,
circumcenter,  nine-point center
nine-point center
- Consider
 with vertices at
with vertices at  ,
,  , and
, and  . Verify that:
. Verify that:
- the circumradius is

 .
.
- the circumradius is