Among the four classical triangle centers — centroid, circumcenter, incenter, orthocenter — only the circumcenter is usually constructed from lines that do not originate from any of the vertices of the parent triangle. It turns out that we can actually alter this tradition, and that’s what we’re after in today’s discussion. We’ll construct lines that originate from each vertex of the parent triangle whose point of concurrence is the circumcenter.

Radial slopes
In ![]() , let
, let ![]() be the slopes of sides
be the slopes of sides ![]() in that order. Let
in that order. Let ![]() be the circumcenter. Then the slope of radius
be the circumcenter. Then the slope of radius ![]() can be given by:
can be given by:
(1) ![]()
Note the position of ![]() , the slope of the side opposite vertex
, the slope of the side opposite vertex ![]() . It’s the key to the “cyclic permutations” that yield similar expressions for the slopes of the radii through vertices
. It’s the key to the “cyclic permutations” that yield similar expressions for the slopes of the radii through vertices ![]() and
and ![]() :
:
(2) 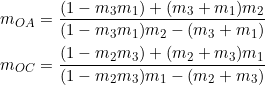
Easy to remember as they all radiate simplicity.
Using the given coordinates:
- the slope of
 is
is 
- the slope of
 is
is 
- the slope of
 is
is 
In order to use equations (1,2), write the side-slopes as ![]() ,
, ![]() ,
, ![]() for
for ![]() ,
, ![]() ,
, ![]() .
.
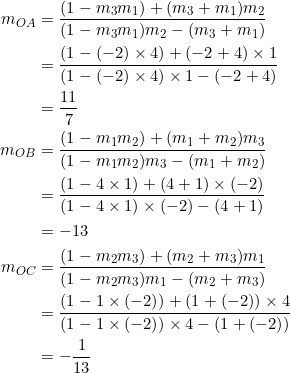
We obtain the same results.
As easy as ![]() . Let
. Let ![]() be such that the slopes of sides
be such that the slopes of sides ![]() are
are ![]() , respectively. By the second equation in (2), the slope of radius
, respectively. By the second equation in (2), the slope of radius ![]() is:
is:
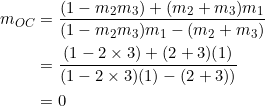
Thus, vertex ![]() shares the same
shares the same ![]() -coordinate as the circumcenter.
-coordinate as the circumcenter. ![]() for common.
for common. ![]() for cool.
for cool.
Similarly, if the slopes of the sides of a triangle are ![]() , then the circumcenter shares the same
, then the circumcenter shares the same ![]() -coordinate with one of the vertices. See the exercises for a more general pattern, and see below for a sample picture:
-coordinate with one of the vertices. See the exercises for a more general pattern, and see below for a sample picture:
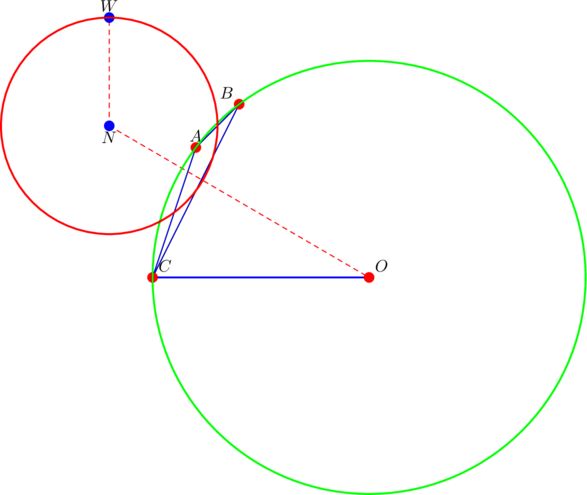
Notice the horizontal radius ![]() , as well as our favourite point
, as well as our favourite point ![]() on the nine-point circle.
on the nine-point circle. ![]() shares the same
shares the same ![]() -coordinate with the nine-point center
-coordinate with the nine-point center ![]() in this case.
in this case.
Let ![]() be such that the slopes of sides
be such that the slopes of sides ![]() are
are ![]() ,
, ![]() ,
, ![]() , respectively. By the second equation in (2), the slope of radius
, respectively. By the second equation in (2), the slope of radius ![]() is:
is:
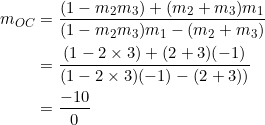
Thus, vertex ![]() has the same
has the same ![]() -coordinate as the circumcenter. Here
-coordinate as the circumcenter. Here ![]() stands for cauton — d0n’t divide by zer0.
stands for cauton — d0n’t divide by zer0.
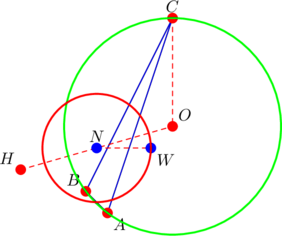
Notice the vertical radius ![]() . Notice also the point
. Notice also the point ![]() on the nine-point circle; it has the same
on the nine-point circle; it has the same ![]() -coordinate as the nine-point center
-coordinate as the nine-point center ![]() in this case.
in this case.
Pick. This. One. Out.
Put ![]() ,
, ![]() , and
, and ![]() for the slopes of sides
for the slopes of sides ![]() ,
, ![]() ,
, ![]() . Consider the slopes of radii
. Consider the slopes of radii ![]() and
and ![]() :
:
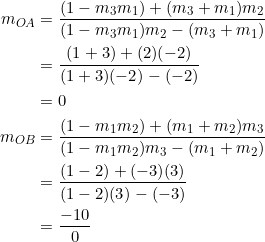
This confirms that radius ![]() is horizontal, while radius
is horizontal, while radius ![]() is vertical. See the exercises for a more general pattern.
is vertical. See the exercises for a more general pattern.
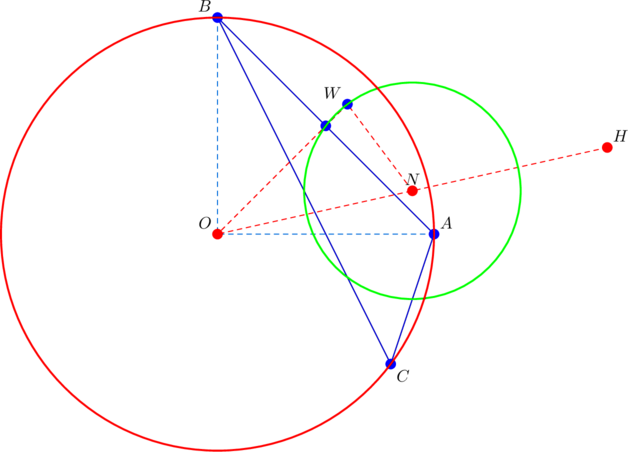
The point ![]() lies on the right bisector of
lies on the right bisector of ![]() in this case. Can you see why we named
in this case. Can you see why we named ![]() the point that
the point that ![]() anders here and there on the nine-point circle?
anders here and there on the nine-point circle?
It’s essential to consider an instance in which one of the slopes of the parent triangle is not well-behaved, as is the case here. We have ![]() ,
, ![]() ,
, ![]() . Notice the slight manoeuvres in the calculations:
. Notice the slight manoeuvres in the calculations:
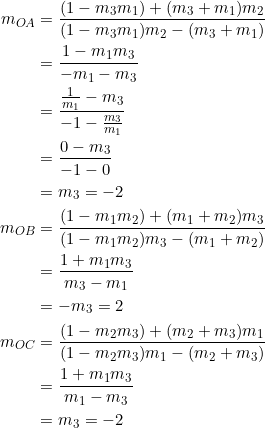
And we obtain a characterization of right triangles with legs parallel to the coordinate axes: a right triangle has legs parallel to the coordinate axes if and only if two of its radii have opposite slopes.
It’s really, really hard to overlook geometric progressions. Let ![]() ,
, ![]() ,
, ![]() be the side-slopes. Then:
be the side-slopes. Then:
- slope of radius
 is:
is: 
- slope of radius
 is:
is: 
- slope of radius
 is:
is: 
So we obtain a geometric progression of the form ![]() , where
, where ![]() or
or ![]() . We must impose another restriction on
. We must impose another restriction on ![]() , namely:
, namely:
![]()
The new common ratio ![]() can equal the original common ratio
can equal the original common ratio ![]() when
when
![]()
Whenever that special quadratic ![]() is sighted, get excited: it signals the presence of an equilateral triangle with slopes in geometric progression. An equilateral triangle. Slopes in geometric progression. Pick them out.
is sighted, get excited: it signals the presence of an equilateral triangle with slopes in geometric progression. An equilateral triangle. Slopes in geometric progression. Pick them out.
If the slopes of the sides of an equilateral triangle form a geometric progression, then so do the slopes of the three radii from the vertices. Furthermore, the two three-term geometric progressions have the same common ratio (but are different because of the ![]() in the middle terms).
in the middle terms).
Radical strategy
Not quite radical per se, but still fundamentally different from — and eventually consistent with — the traditional method for finding the circumcenter. Our technique is merely intended to demonstrate what’s possible in principle; for practical computational purposes it’s inconvenent, and so not recommended.
Here ![]() ,
, ![]() , and
, and ![]() as per the slopes of
as per the slopes of ![]() ,
, ![]() ,
, ![]() . Using equations (1,2), we obtain the slopes of the three lines (not proper to call them radii yet):
. Using equations (1,2), we obtain the slopes of the three lines (not proper to call them radii yet):
![]()
and hence the equations of the three lines:
(3) 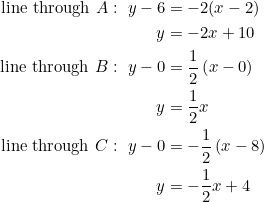
Consider the equations of the lines through ![]() and
and ![]() :
:
![]()
The pair ![]() also satisfies the equation of the line through
also satisfies the equation of the line through ![]() :
:
![]()
Thus, the three equations are consistent and the circumcenter is therefore located at ![]() .
.
Don’t use ths method in real life.
Here we’re jumping the gun by calling radii, but don’t mind. We have ![]() ,
, ![]() , and
, and ![]() as per the slopes of
as per the slopes of ![]() ,
, ![]() ,
, ![]() . Using equations (1,2), we obtain the slopes of the three radii:
. Using equations (1,2), we obtain the slopes of the three radii:
![]()
and hence the equations of the three radii:
(4) 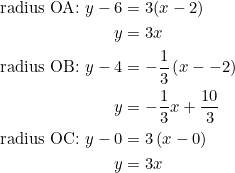
Consider the equations of radii ![]() and
and ![]() :
:
![]()
The pair ![]() also satisfies the equation of radius
also satisfies the equation of radius ![]() :
:
![]()
Thus, the three equations are consistent and the circumcenter is therefore located at ![]() .
.
Notice that ![]() is the midpoint of
is the midpoint of ![]() . So the parent triangle is right-angled.
. So the parent triangle is right-angled.
Right scenario
Today’s discussion bodes well for right triangles.
Let ![]() . According to equation (2):
. According to equation (2):
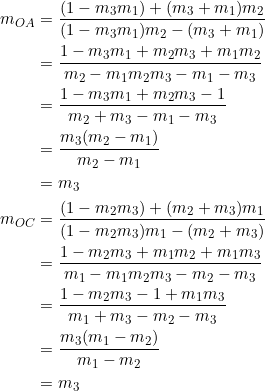
Can you see how this verifies that the circumcenter of a right triangle must lie on the hypotenuse? The slope way.
Suppose that the slope of radius ![]() is equal to the slope of radius
is equal to the slope of radius ![]() . By equations (1,2):
. By equations (1,2):
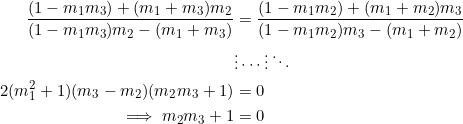
A couple of steps were skipped, but you get the gist.
Takeaway
The three statements below are equivalent for any triangle:
- the triangle is a right triangle or this triangle
- the slopes of two radii are equal
- one radius and one side have the same slope.
Tasks
- Find a triangle
 in which the slopes of its three radii are equal to the negatives of the slopes of its three sides.
in which the slopes of its three radii are equal to the negatives of the slopes of its three sides. - Give an example of a right triangle having one radius horizontal and another radius vertical.
- Let
 be an arbitrary triangle with circumcenter
be an arbitrary triangle with circumcenter  .
.
- If side
 has slope
has slope  , PROVE that the slopes of the radii
, PROVE that the slopes of the radii  and
and  are reciprocals of each other.
are reciprocals of each other. - If side
 has slope
has slope  , PROVE that the slopes of the radii
, PROVE that the slopes of the radii  and
and  are negatives of each other.
are negatives of each other.
- If side
- In
 , Let
, Let  be the slopes of sides
be the slopes of sides  , and let the circumcenter be
, and let the circumcenter be  .
.
- PROVE that there’s a horizontal radius if
 . Which of the radii
. Which of the radii  will it be?
will it be? - PROVE that there’s a vertical radius if
 . Which of the radii
. Which of the radii  will it be?
will it be? - Deduce that a circumcenter cannot coincide with a vertex, unless the triangle is a single point.
- PROVE that there’s a horizontal radius if
- (Pattern recognition) Suppose that the set
 of slopes produce a horizontal radius, in light of the previous exercise. PROVE that each of the following sets of slopes also produce a horizontal radius:
of slopes produce a horizontal radius, in light of the previous exercise. PROVE that each of the following sets of slopes also produce a horizontal radius:
- (Perpendicular radii) Suppose that radii
 and
and  are perpendicular. As usual, let
are perpendicular. As usual, let  ,
,  ,
,  be the slopes of sides
be the slopes of sides  ,
,  ,
,  .
.
- PROVE that

- Deduce that
 or
or 
- If
 , deduce that one of the radii
, deduce that one of the radii  or
or  is horizontal and the other vertical.
is horizontal and the other vertical.
- PROVE that
- (Principal result) Here’s how to obtain the main result of our discussion. In
 , let
, let  be the slopes of sides
be the slopes of sides  , and let the circumcenter be
, and let the circumcenter be  . Suppose that
. Suppose that  .
.
- If
 is inside the parent triangle, PROVE that
is inside the parent triangle, PROVE that  is
is 
- If
 is outside the parent triangle, PROVE that
is outside the parent triangle, PROVE that  is
is 
- Derive equation (1).
- If
- In
 , Let
, Let  be the slopes of sides
be the slopes of sides  .
.
- Suppose that
 . PROVE that the slope of the radius
. PROVE that the slope of the radius  is
is  . In particular, if
. In particular, if  , deduce that the diameter through vertex
, deduce that the diameter through vertex  is vertical.
is vertical. - Suppose that
 . PROVE that the slope of the radius
. PROVE that the slope of the radius  is
is  . In particular, if
. In particular, if  , deduce that the diameter through vertex
, deduce that the diameter through vertex  is horizontal.
is horizontal.
- Suppose that
- PROVE that any triangle with side-slopes
 contains:
contains:
- a horizontal radius
- a vertical median. (A vertical median always shows up when the side-slopes form an arithmetic progression, like
 .)
.)
- PROVE a result similar to that of exercise 5 above in the case of vertical radius.