Let ![]() be the centroid of
be the centroid of ![]() Denote by
Denote by ![]() the centroids of triangles
the centroids of triangles ![]() , respectively. Then the lines
, respectively. Then the lines ![]() are concurrent at
are concurrent at ![]() , the centroid of the parent triangle.
, the centroid of the parent triangle.
Further, let ![]() be the circumcenter of
be the circumcenter of ![]() . Denote by
. Denote by ![]() the circumcenters of triangles
the circumcenters of triangles ![]() , in that order. According to Kosnita’s theorem, the lines
, in that order. According to Kosnita’s theorem, the lines ![]() are concurrent at a point called the Kosnita point.
are concurrent at a point called the Kosnita point.
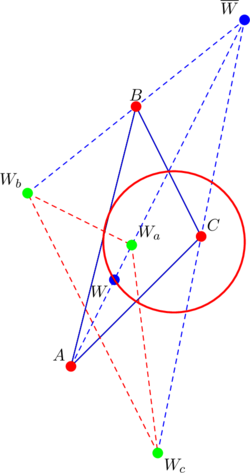
Now let ![]() be that point that wanders here and there on the nine-point circle of
be that point that wanders here and there on the nine-point circle of ![]() (coordinates given by (1) or (2) or (3) or (4)). Denote by
(coordinates given by (1) or (2) or (3) or (4)). Denote by ![]() the “
the “![]() -centers” of triangles
-centers” of triangles ![]() respectively. In this post we show that the lines
respectively. In this post we show that the lines ![]() are concurrent, if the slopes of the parent triangle form a geometric progression.
are concurrent, if the slopes of the parent triangle form a geometric progression.
(1) 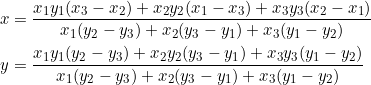
(2) ![]()
(3) ![]()
(4) ![]()
![]() are the coordinates of the vertices, while
are the coordinates of the vertices, while ![]() are the slopes of sides
are the slopes of sides ![]() . Equations (2),(3),(4) are all equivalent (to (1)) representations of point
. Equations (2),(3),(4) are all equivalent (to (1)) representations of point ![]() .
.
Concurrence
Throughout, ![]() will denote the “W-center” of
will denote the “W-center” of ![]() , while
, while ![]() represent the “W-centers” of triangles
represent the “W-centers” of triangles ![]() .
.
Let the slopes of ![]() be
be ![]() in that order. Since
in that order. Since ![]() is constructed from
is constructed from ![]() , the slope of
, the slope of ![]() is the product of the slopes of
is the product of the slopes of ![]() and
and ![]() , divided by the negative of the slope of
, divided by the negative of the slope of ![]() (the way it works in general, as shown in this post, is as follows: take the product of the slopes of the two sides that originate from the reference vertex and then divide by the negative of the slope of the opposite side).
(the way it works in general, as shown in this post, is as follows: take the product of the slopes of the two sides that originate from the reference vertex and then divide by the negative of the slope of the opposite side).
(5) 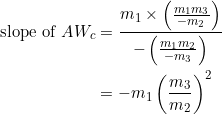
Similarly, the slope of ![]() is the product of the slopes of
is the product of the slopes of ![]() and
and ![]() , divided by the negative of the slope of
, divided by the negative of the slope of ![]() :
:
(6) 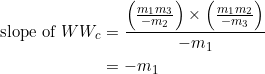
As before, let ![]() be the slopes of sides
be the slopes of sides ![]() respectively. Since
respectively. Since ![]() is constructed from
is constructed from ![]() , the slope of
, the slope of ![]() is the product of the slopes of
is the product of the slopes of ![]() and
and ![]() , divided by the negative of the slope of
, divided by the negative of the slope of ![]() :
:
(7) 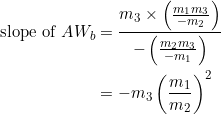
Similarly, the slope of ![]() is the product of the slopes of
is the product of the slopes of ![]() and
and ![]() , divided by the negative of the slope of
, divided by the negative of the slope of ![]() :
:
(8) 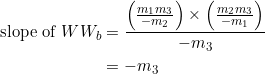
Set ![]() . From equation (5):
. From equation (5):
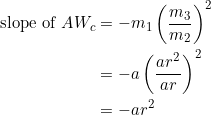
From equation (6):
![]()
From equation (7):
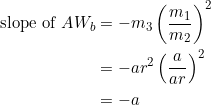
From equation (8):
![]()
Thus, ![]() is parallel to
is parallel to ![]() , and
, and ![]() is parallel to
is parallel to ![]() . There the parallelogram
. There the parallelogram ![]() goes.
goes.
We’ve already seen that ![]() lies on the median through vertex
lies on the median through vertex ![]() in example 6 here.
in example 6 here.
To see that ![]() also lies on the median through vertex
also lies on the median through vertex ![]() , recall that
, recall that ![]() was constructed from
was constructed from ![]() . As such, the slope of the line
. As such, the slope of the line ![]() is the product of the slopes of
is the product of the slopes of ![]() and
and ![]() divided by the negative of the slope of
divided by the negative of the slope of ![]() :
:
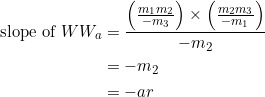
The slope of the median through vertex ![]() is
is ![]() , the slope of
, the slope of ![]() is also
is also ![]() , and the slope of
, and the slope of ![]() is again
is again ![]() . Thus, the points
. Thus, the points ![]() are co-linear together with the midpoint of
are co-linear together with the midpoint of ![]() .
.
(Main goal)
First consider the segment ![]() . In the parallelogram constructed in example 3,
. In the parallelogram constructed in example 3, ![]() and
and ![]() are diagonals, so their midpoints coincide. Next, draw the lines
are diagonals, so their midpoints coincide. Next, draw the lines ![]() and
and ![]() and extend till they intersect at
and extend till they intersect at ![]() , say. We claim that the line
, say. We claim that the line ![]() also passes through
also passes through ![]() . This follows because the midpoint of
. This follows because the midpoint of ![]() lies on the median through
lies on the median through ![]() — as do
— as do ![]() and
and ![]() — so the line
— so the line ![]() will go through
will go through ![]() (in fact, it is a median — extended if necessary — in
(in fact, it is a median — extended if necessary — in ![]() ).
).
As usual, let the slopes be ![]() for sides
for sides ![]() . Consider
. Consider ![]() for example. In equation (6) we saw that the slope of
for example. In equation (6) we saw that the slope of ![]() , the negative of the slope of side
, the negative of the slope of side ![]() . In equation (8) we saw that the slope of
. In equation (8) we saw that the slope of ![]() , the negative of the slope of
, the negative of the slope of ![]() . Thus, the angle between
. Thus, the angle between ![]() and
and ![]() is either angle
is either angle ![]() itself, or its supplement.
itself, or its supplement.
Coordinates
In the case of triangles with slopes in geometric progression ![]() , we’re able to explicitly determine the coordinates of the point of concurrence of the lines
, we’re able to explicitly determine the coordinates of the point of concurrence of the lines ![]() ,
, ![]() ,
, ![]() :
:
(9) 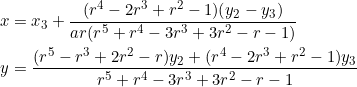
How does one identify ![]() from a given triangle? Well, easy: just arrange the slopes in such a way that they appear in the format
from a given triangle? Well, easy: just arrange the slopes in such a way that they appear in the format ![]() for sides
for sides ![]() respectively. Then
respectively. Then ![]() are the coordinates of vertex
are the coordinates of vertex ![]() and
and ![]() is the
is the ![]() -coordinate of
-coordinate of ![]() . (Notice how the coefficients of
. (Notice how the coefficients of ![]() and
and ![]() in the second equation in (9) add up to the denominator. So in a sense, they’re “weighted”.)
in the second equation in (9) add up to the denominator. So in a sense, they’re “weighted”.)
The slopes of sides ![]() are
are ![]() in that order; they form a geometric progression of the form
in that order; they form a geometric progression of the form ![]() . As specified in equation (9), we identify
. As specified in equation (9), we identify ![]() ,
, ![]() , and
, and ![]() .
.
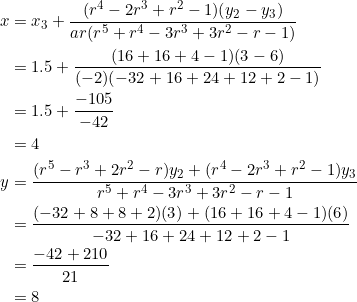
The point of concurrence is at ![]() as shown below:
as shown below:
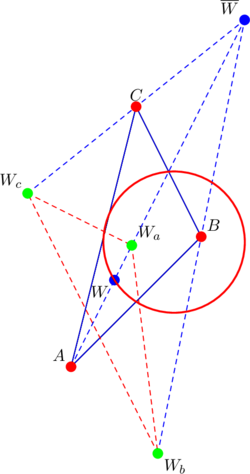
Notice point ![]() on the nine-point circle of the parent triangle
on the nine-point circle of the parent triangle ![]() . Points
. Points ![]() ,
, ![]() ,
, ![]() also lie on the nine-point circles of triangles
also lie on the nine-point circles of triangles ![]() ,
, ![]() ,
, ![]() .
.
In the exercises we ask you to derive the following equation:
(10) ![]()
Don’t be intimidated by equation (10), especially with the slope terms ![]() that appear there; its derivation can be accomplished without coordinates. In fact, triangles
that appear there; its derivation can be accomplished without coordinates. In fact, triangles ![]() ,
, ![]() ,
, ![]() always have their slopes in geometric progressions — irrespective of what happens in the parent triangle
always have their slopes in geometric progressions — irrespective of what happens in the parent triangle ![]() (exception: when one side of the parent triangle is parallel to the
(exception: when one side of the parent triangle is parallel to the ![]() or
or ![]() axis) — and so a certain approximate pythagorean identity can be applied to derive equation (10).
axis) — and so a certain approximate pythagorean identity can be applied to derive equation (10).
The side-lengths ![]() satisfy an approximate pythagorean identity:
satisfy an approximate pythagorean identity:
![]()
Using equation (10) with ![]() ,
, ![]() , and
, and ![]() :
:
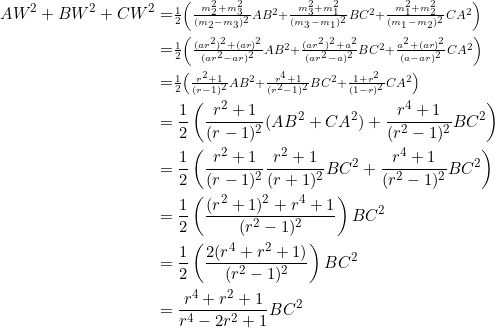
We had, from the preceding example, that:
![]()
In a previous post we asked you to prove that
![]()
Combine these two equations:
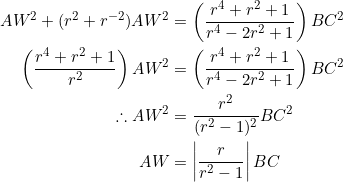
Can you guess a value of ![]() for which
for which ![]() ? There it goes — it’s that golden ratio thing.
? There it goes — it’s that golden ratio thing.
Coincidence
And a cauton.
Observe that the slopes of sides ![]() are
are ![]() ; they do not form a geometric progression (even when re-arranged as
; they do not form a geometric progression (even when re-arranged as ![]() ). So this example suggests that there are other instances of concurrence of the lines
). So this example suggests that there are other instances of concurrence of the lines ![]() ,
, ![]() ,
, ![]() beyond geometric progressions.
beyond geometric progressions.
- the “W-center” of the parent triangle is
 — obtained by solving the consistent equations
— obtained by solving the consistent equations  ,
,  ,
, 
- the “W-center” of
 is
is  — obtained by solving the consistent system
— obtained by solving the consistent system  ,
,  ,
,  . Using
. Using  and
and  , we obtain the equation
, we obtain the equation  as the equation of line
as the equation of line 
- the “W-center” of
 is
is  — obtained by solving the consistent system
— obtained by solving the consistent system  ,
,  ,
,  . Using
. Using  and
and  , we obtain the equation
, we obtain the equation  for the line
for the line  — incidentally, this is also the equation of line
— incidentally, this is also the equation of line 
- the “W-center” of
 is
is  — obtained by solving the consistent system
— obtained by solving the consistent system  ,
,  ,
,  . Using
. Using  and
and  , we obtain the equation
, we obtain the equation  — which, incidentally, is the equation of line
— which, incidentally, is the equation of line  . Together with the preceding incidence, we obtain a coincidence
. Together with the preceding incidence, we obtain a coincidence - the equations of lines
 ,
,  ,
,  are
are  ,
,  ,
,  . These three lines concur at
. These three lines concur at  — coordinates of vertex
— coordinates of vertex  . C for coincidence. C for caution.
. C for coincidence. C for caution.
Takeaway
In ![]() , let
, let ![]() be the slopes of sides
be the slopes of sides ![]() . Let
. Let ![]() be that point on the nine-point circle whose coordinates are given by equation (1). Then the four statements below are equivalent:
be that point on the nine-point circle whose coordinates are given by equation (1). Then the four statements below are equivalent:


 or
or 

You can see the golden ratio popping up in the third statement above. That seemingly ubiquitous golden ratio thing is increasingly becoming conspicuous in our theory.
Tasks
- Find a triangle
 and a point
and a point  on its nine-point circle such that
on its nine-point circle such that  .
. - In
 , Let
, Let  be the slopes of sides
be the slopes of sides  . Let
. Let  be the point whose coordinates were given in equation (1). PROVE that:
be the point whose coordinates were given in equation (1). PROVE that:
- (Coordinates) Use equation (2) to prove that the “W-center” of
 is
is 
- (Congruence) In
 , let
, let  be points that are diametrically opposite vertices
be points that are diametrically opposite vertices  , respectively. PROVE that:
, respectively. PROVE that:
 is congruent to
is congruent to 
- the “W” center of
 and the “W-center” of
and the “W-center” of  have their midpoint at the circumcenter of the parent
have their midpoint at the circumcenter of the parent 
(In general, it’s a similar scenario with the orthocenter and co — all due to a certain homothecy centered at the circumcenter .)
.)
- (Coincidence) Let
 be such that
be such that  is parallel to the
is parallel to the  -axis, and
-axis, and  and
and  have reciprocal slopes. PROVE that:
have reciprocal slopes. PROVE that:
- the Kosnita point coincides with vertex

- the point
 diametrically opposite this Kosnita point forms an isosceles trapezoid
diametrically opposite this Kosnita point forms an isosceles trapezoid  in conjuction with the other points.
in conjuction with the other points.
- the Kosnita point coincides with vertex
- (Concurrent coincidence)
 has vertices at
has vertices at  ,
,  ,
,  . PROVE that:
. PROVE that:
-
 is the point
is the point 
 is the point
is the point 
 is the point
is the point 
 is the point
is the point 
- the point of concurrence of the lines
 ,
,  ,
,  is
is  .
.
-
- In any triangle
 , PROVE that:
, PROVE that:
- the slope of
 is the negative of the slope of
is the negative of the slope of 
- the slope of
 is the negative of the slope of
is the negative of the slope of 
- the slope of
 is the negative of the slope of
is the negative of the slope of 
- the slope of
- Given a triangle
 with side-slopes
with side-slopes  , find a triangle with side-slopes
, find a triangle with side-slopes  ,
,  ,
,  .
.
(Hint: Consider .)
.) - If the slopes of sides
 form a geometric progression
form a geometric progression  , PROVE that
, PROVE that  is parallel to side
is parallel to side  .
. - PROVE that
 .
.