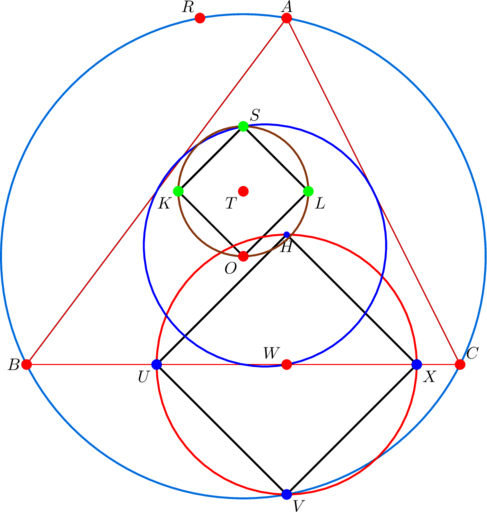
Look at the diagram above, where a number of things appear to be happening. The red circle that goes through points ![]() is our focus for now. The center
is our focus for now. The center ![]() of this circle is itself a point on the nine-point circle of the parent
of this circle is itself a point on the nine-point circle of the parent ![]() . We’ll examine more of the properties of
. We’ll examine more of the properties of ![]() in this post, especially when the side-slopes of
in this post, especially when the side-slopes of ![]() form a geometric progression.
form a geometric progression.
Simplified coordinates
If ![]() has vertices at
has vertices at ![]() ,
, ![]() ,
, ![]() , then the coordinates of point
, then the coordinates of point ![]() are given by:
are given by:
(1) 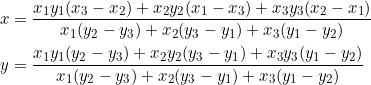
Compare (1) with its equivalent, simplified version:
(2) ![]()
Here, ![]() are the slopes of sides
are the slopes of sides ![]() , respectively. Notice that
, respectively. Notice that ![]() and the coordinates of
and the coordinates of ![]() are explicitly “missing” in equation (2). One implication is that the calculation of
are explicitly “missing” in equation (2). One implication is that the calculation of ![]() requires only two sides and the slopes of those two sides. So (2) can take another form:
requires only two sides and the slopes of those two sides. So (2) can take another form:
(3) ![]()
(4) ![]()
Ample freedom. Simple concept.
Set ![]() ,
, ![]() , and
, and ![]() . The slopes of sides
. The slopes of sides ![]() , and
, and ![]() are then
are then ![]() ,
, ![]() , and
, and ![]() , respectively.
, respectively.
Using equation (2):
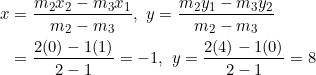
Using equation (3):
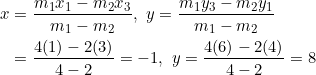
Using equation (4):
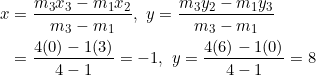
In each case we obtain ![]() . It’s that point that
. It’s that point that ![]() anders here and there on the nine-point circle.
anders here and there on the nine-point circle.
The converse is also true. Fix the vertices at ![]() ,
, ![]() ,
, ![]() . Let the slopes of
. Let the slopes of ![]() be
be ![]() and suppose that
and suppose that ![]() . Using equation (2):
. Using equation (2):
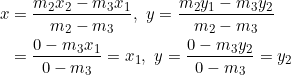
Thus, ![]() is the point
is the point ![]() , which is the foot of the altitude from vertex
, which is the foot of the altitude from vertex ![]() .
.
The converse is also true. Fix the vertices at ![]() ,
, ![]() ,
, ![]() . Let the slopes of
. Let the slopes of ![]() be
be ![]() and suppose that
and suppose that ![]() . Using equation (2):
. Using equation (2):
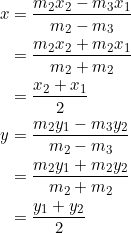
Thus, ![]() is the point
is the point ![]() , which is the midpoint of
, which is the midpoint of ![]() .
.
This follows from example 3, since ![]() are opposites.
are opposites.
Special case
Most of our points behave extremely well if the side-slopes of the parent triangle form a geometric progression. Expectedly, our favorite point ![]() is not an exception.
is not an exception.
Let the slopes of sides ![]() be
be ![]() ,
, ![]() ,
, ![]() . From this post, the slopes from
. From this post, the slopes from ![]() to vertices
to vertices ![]() are:
are:
(5) 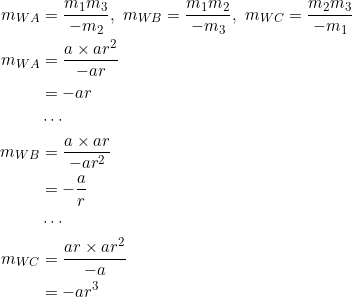
Thus, ![]() correspond to the geometric progression
correspond to the geometric progression ![]() with common ratio
with common ratio ![]() .
.
From the preceding example, the slope from ![]() to vertex
to vertex ![]() is
is ![]() . From this post, the slope from vertex
. From this post, the slope from vertex ![]() to the midpoint of side
to the midpoint of side ![]() is also
is also ![]() . Thus,
. Thus, ![]() lies on the median through vertex
lies on the median through vertex ![]() .
.
As noted in example 6 above, the point ![]() is on the median through vertex
is on the median through vertex ![]() . Suppose that
. Suppose that ![]() lies outside the triangle (usually when
lies outside the triangle (usually when ![]() ). Let
). Let ![]() be the midpoint of side
be the midpoint of side ![]() . Then the area of
. Then the area of ![]() is equal to the area of
is equal to the area of ![]() (since
(since ![]() is a median in
is a median in ![]() ). But then the area of
). But then the area of ![]() is also equal to the area of
is also equal to the area of ![]() (since
(since ![]() is a median in
is a median in ![]() ). Together we have that the area of
). Together we have that the area of ![]() is equal to the area of
is equal to the area of ![]() . Same conclusion when
. Same conclusion when ![]() is inside the parent triangle.
is inside the parent triangle.
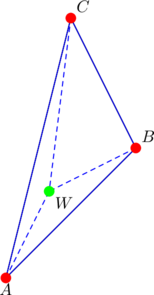
In the diagram above, point ![]() is inside the given triangle. The areas of triangles
is inside the given triangle. The areas of triangles ![]() and
and ![]() are equal.
are equal.
Sample calculations
Since ![]() lies on the median through vertex
lies on the median through vertex ![]() , it is natural to ask what ratio both it and the centroid
, it is natural to ask what ratio both it and the centroid ![]() divide the entire median length
divide the entire median length ![]() .
.
(6) ![]()
As you already know, the relations in (6) hold when the slopes of the parent triangle form a geometric progression. Absolute values may be necessary in some cases.
The common ratio ![]() of the slopes
of the slopes ![]() of an equilateral triangle satisfies the quadratic equation
of an equilateral triangle satisfies the quadratic equation
(7) ![]()
Use equation (7) and the first ratio in equation (6) to obtain
![]()
Thus, ![]() and so
and so ![]() is the midpoint of
is the midpoint of ![]() and
and ![]() . In addition, since the centroid divides median
. In addition, since the centroid divides median ![]() in the ratio
in the ratio ![]() , it follows that
, it follows that ![]() in this case.
in this case.
Use the first ratio in equation (6) and the fact that the common ratio of the slopes ![]() of a right isosceles triangle satisfies the quadratic equation
of a right isosceles triangle satisfies the quadratic equation
(8) ![]()
and obtain
![]()
Thus, ![]() .
.
We have:
![]()
Thus, the line segment ![]() is longer than the median
is longer than the median ![]() . (If
. (If ![]() , we can’t conclude that
, we can’t conclude that ![]() lies inside the triangle.)
lies inside the triangle.)
Takeaway
In ![]() , let
, let ![]() be the centroid,
be the centroid, ![]() the midpoint of side
the midpoint of side ![]() , and
, and ![]() as given by equation (1). If the slopes of sides
as given by equation (1). If the slopes of sides ![]() form a geometric progression
form a geometric progression ![]() then the following statements are equivalent:
then the following statements are equivalent:
 , where
, where  is the sum of quotients of slopes defined here
is the sum of quotients of slopes defined here or
or 
 or
or 
 or
or 
 or
or  or
or  or
or  , where
, where  is the golden ratio
is the golden ratio or
or 
 or
or 
 or
or  .
.
Eight easy equivalences. A triangle that satisfies any of these (together with ![]() or
or ![]() ) will be a right isosceles triangle (or its “look-alike”).
) will be a right isosceles triangle (or its “look-alike”).
Tasks
- Let
 be such that
be such that  is parallel to the
is parallel to the  -axis, and
-axis, and  and
and  have reciprocal slopes. PROVE that:
have reciprocal slopes. PROVE that:
- the orthocenter
 is a reflection of vertex
is a reflection of vertex  across the
across the  -axis
-axis  is the foot of the altitude from vertex
is the foot of the altitude from vertex 
 is the midpoint of
is the midpoint of  and
and 
- the orthocenter
- Let
 be the slopes of the line segments from
be the slopes of the line segments from  to the vertices of
to the vertices of  , and let
, and let  be the side-slopes.
be the side-slopes.
- PROVE that
 .
. - If
 is right-angled, deduce that the product
is right-angled, deduce that the product  equals the slope of the hypotenuse.
equals the slope of the hypotenuse.
- PROVE that
- PROVE that
 for any
for any  with side-slopes
with side-slopes  .
. - Find coordinates for the vertices of
 having the property that a point
having the property that a point  on its nine-point circle is twice as far from vertex
on its nine-point circle is twice as far from vertex  as it is from the centroid
as it is from the centroid  .
. - Suppose that the slopes of sides
 are
are  , in that order. Let
, in that order. Let  be as given in equation (1), and let
be as given in equation (1), and let  be the midpoint of
be the midpoint of  . PROVE that
. PROVE that  .
.