Extra points
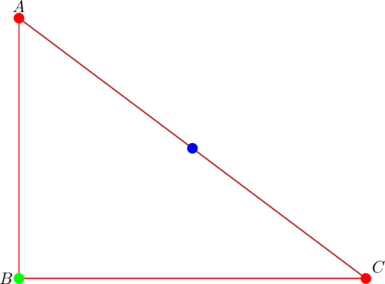
Our intention at the beginning of the year was to focus most of our attention on four points ![]() associated with any triangle, depicted below:
associated with any triangle, depicted below:
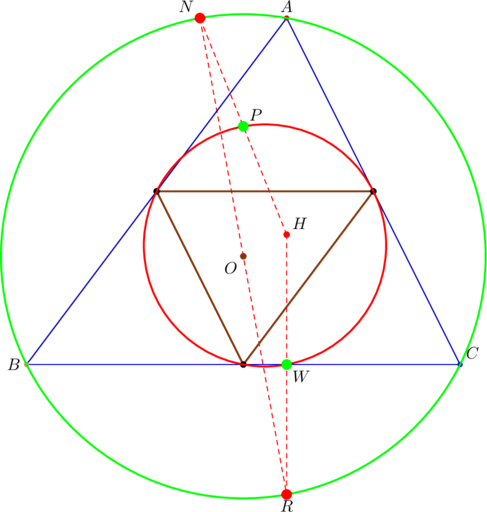
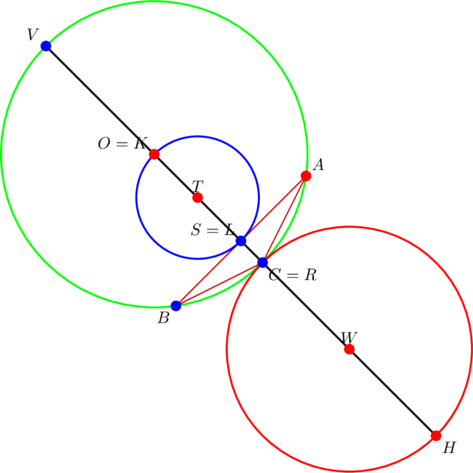
By March, much has changed, and we’re grateful to be able to add seven more points, bringing the total, as at this paragraph, to eleven:
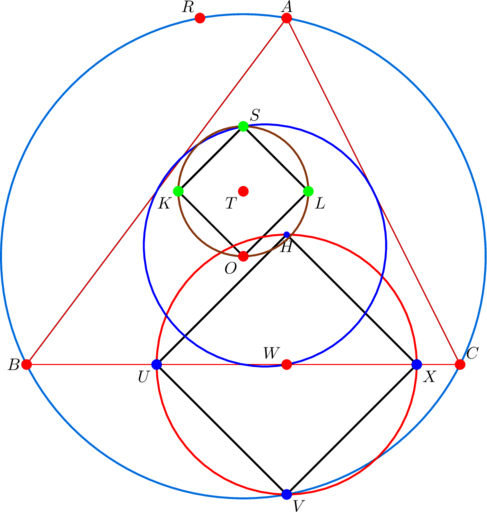
Actually, we have fourteen more points, so that the total, as at the time of this writing, is twenty five. However, these other fourteen points behave totally differently from the above mentioned eleven.
Extended period
Following the addition of twenty one extra points, our initial one-year time frame has been affected. Please help us do the math: “If it takes one year to discuss four points, how long will it take to discuss twenty five points, assuming it takes the same length of time for each point”?
Exchanging pleasantries
Welcome to our theory!
Extensive properties
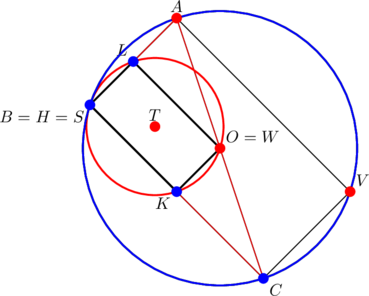
With reference to the preceding diagram, we have the following individual and collective properties of the points:
- each point is a point of concurrency of some lines (in this post we show how to obtain
 ; in the future, we’ll feature how to obtain the rest)
; in the future, we’ll feature how to obtain the rest)  and
and  are on the circumcircle of the parent
are on the circumcircle of the parent  (in fact,
(in fact,  is a diameter)
is a diameter) and
and  are on the nine-point circle of the parent
are on the nine-point circle of the parent  (in fact,
(in fact,  is a diameter)
is a diameter)- the line segments
 always make an angle of
always make an angle of  with the positive
with the positive  -axis
-axis - the line segments
 always make an angle of
always make an angle of  with the positive
with the positive  -axis
-axis - quadrilaterals
 and
and  are always rectangles (follows from the previous two)
are always rectangles (follows from the previous two) - the two rectangles
 and
and  are “parallel”
are “parallel” - the area of the bigger rectangle
 is four times the area of the smaller rectangle
is four times the area of the smaller rectangle 
 is the center of the cyclic quadrilateral
is the center of the cyclic quadrilateral 
 is the center of the cyclic quadrilateral
is the center of the cyclic quadrilateral 
- rectangles
 and
and  can become squares in special cases (in particular, the extremely pleasant case of a triangle having two sides with reciprocal slopes and one side parallel to the
can become squares in special cases (in particular, the extremely pleasant case of a triangle having two sides with reciprocal slopes and one side parallel to the  -axis, and in the expectedly peculiar case of an equilateral triangle)
-axis, and in the expectedly peculiar case of an equilateral triangle) - if points
 are connnected to form
are connnected to form  , then the Euler line
, then the Euler line  is just a median in this triangle
is just a median in this triangle - if the legs of a right triangle are parallel to the coordinate axes, then rectangle
 becomes just the circumcenter and rectangle
becomes just the circumcenter and rectangle  becomes the orthocenter (this is a degenerate case, but it does generate additional characterizations of this particular right triangle)
becomes the orthocenter (this is a degenerate case, but it does generate additional characterizations of this particular right triangle) - if the slopes of the sides of the parent
 form a geometric progression, then rectangles
form a geometric progression, then rectangles  and
and  “sit” on the same line (the case of geometric progressions is the exquisite platform for the present concept)
“sit” on the same line (the case of geometric progressions is the exquisite platform for the present concept) - our favourite point is the wandering point
 (this isn’t a property though, but there’s a basis for our bias)
(this isn’t a property though, but there’s a basis for our bias) - And lots more! (this isn’t a property either, but as we explore these points in future posts, more will be shown).
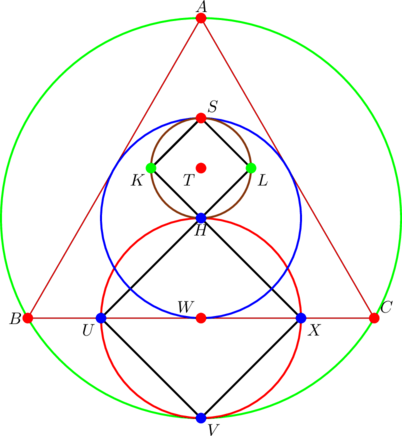
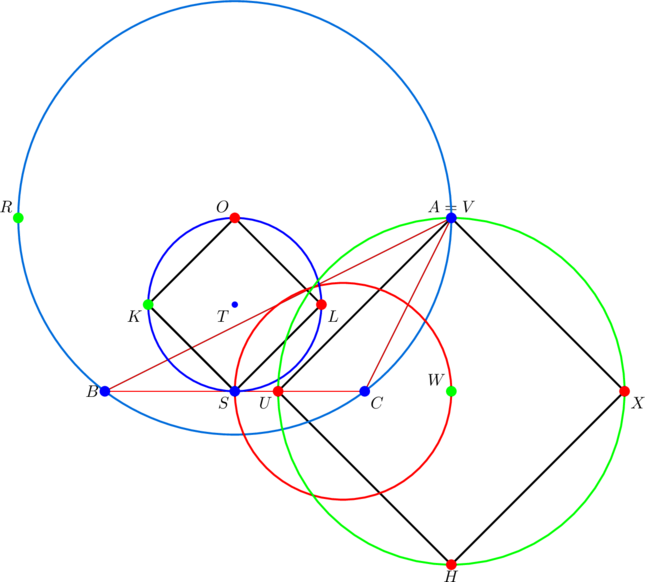

Elementary proofs
Using an idea from our last post, we’ll now define the three lines that have point ![]() as a point of concurrency.
as a point of concurrency.
Define lines from ![]() as follows: the line from
as follows: the line from ![]() has slope
has slope ![]() , the line from
, the line from ![]() has slope
has slope ![]() , and the line from
, and the line from ![]() has slope
has slope ![]() .
.
PROVE that the three lines defined above are concurrent.
Consider two such lines through ![]() and
and ![]() .
.
(1) 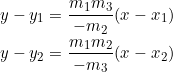
The solution to the linear system (1) is:
![]()
Let’s verify concurrency. We’ll prove that the solution above satisfies the equation of the line through ![]() :
:
(2) ![]()
Note that
![]()
Consider the left member of equation (2):
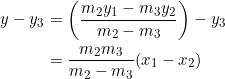
Now consider the right member of equation (2):
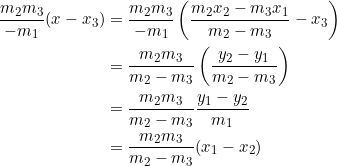
Admittedly, we skipped a couple of steps, probably because we didn’t want to focus on the details of the algebra, but instead on how the lines were defined. Now go ahead and alter our definition to obtain other points of concurrency.
Given ![]() with vertices at
with vertices at ![]() ,
, ![]() ,
, ![]() , the point
, the point ![]() is on its nine-point circle. Find the equations of the three lines through
is on its nine-point circle. Find the equations of the three lines through ![]() that intersect at
that intersect at ![]() .
.
The slopes of ![]() are
are ![]() . Set
. Set
![]()
and define lines through ![]() with slopes
with slopes ![]() , respectively:
, respectively:
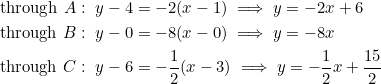
These three equations are all satisfied by ![]() .
.
Given ![]() with vertices at
with vertices at ![]() ,
, ![]() ,
, ![]() , define lines through the midpoints of
, define lines through the midpoints of ![]() in such a way that the slopes are negatives of the slopes of the sides. PROVE that the three lines meet at the point
in such a way that the slopes are negatives of the slopes of the sides. PROVE that the three lines meet at the point ![]() .
.
This is actually an interesting property. Basically, we can obtain the point ![]() in two different ways:
in two different ways:
- through each vertex, draw lines with slopes of the form
 , where
, where  is the slope of the side opposite the reference vertex
is the slope of the side opposite the reference vertex - through each midpoint, draw lines with slopes that are negatives of the slopes of the sides on which the midpoints lie.
In the present case, the slopes of ![]() are
are ![]() , and the midpoints are
, and the midpoints are ![]() ,
, ![]() , and
, and ![]() , respectively. Through each of these midpoints we draw lines with slopes
, respectively. Through each of these midpoints we draw lines with slopes ![]() :
:
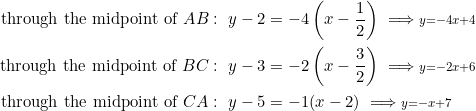
These three equations are all satisfied by ![]() .
.
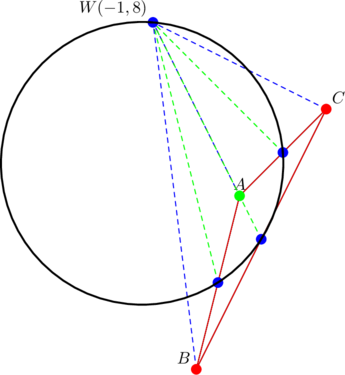
The point ![]() on the nine-point circle of
on the nine-point circle of ![]() .
.
Eventful pi
Our final example is a big digression from the preceding discussion. For your pi day celebration.
Let ![]() be the side-lengths, and let
be the side-lengths, and let ![]() be the nine-point center, of non-right
be the nine-point center, of non-right ![]() . If
. If ![]() and
and ![]() , PROVE that
, PROVE that ![]() .
.
And so a different version of “![]() ” for your pi day celebration.
” for your pi day celebration.
Let ![]() be the circumradius. Since
be the circumradius. Since
![]()
we have ![]() Further simplifications:
Further simplifications:
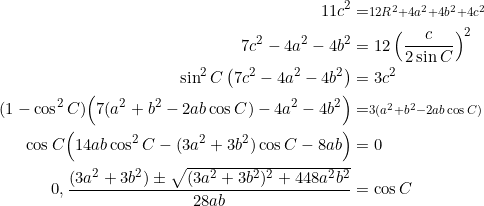
Since ![]() is not a right triangle (right triangles automatically satisfy the relation
is not a right triangle (right triangles automatically satisfy the relation ![]() if
if ![]() is taken as the hypotenuse), we ignore the
is taken as the hypotenuse), we ignore the ![]() value. Then put
value. Then put ![]() and consider the negative discriminant (the positive part would give
and consider the negative discriminant (the positive part would give ![]() , unacceptable):
, unacceptable):
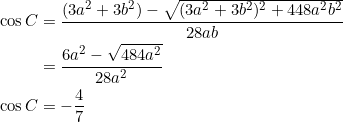
By the cosine law again:
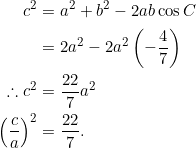
There ![]() goes.
goes.
Takeaway
The following statements are equivalent for any ![]() :
:
 , where
, where  is the orthocenter
is the orthocenter- two sides of the triangle are parallel to the coordinate axes
 coincides with one of the triangle’s vertices
coincides with one of the triangle’s vertices- the slopes of the three medians form a geometric progression with common ratio

- the slopes of the three medians form an arithmetic progression with common difference equal to
 times the first term (
times the first term ( )
) - one side of the triangle is parallel to the
 -axis and another side and the median to it have opposite slopes.
-axis and another side and the median to it have opposite slopes.
You’re already familiar with the above six equivalent statements. By the time we finish discussing our new points, the number of characterizations will be about twenty, if not more. Be looking forward to that time.
Tasks
- Given
 with vertices
with vertices  ,
,  ,
,  , and
, and  as the slopes of sides
as the slopes of sides  , respectively, PROVE that:
, respectively, PROVE that:
-
- PROVE that the line segments from
 to the three vertices and the three midpoints either all make acute angles with the positive
to the three vertices and the three midpoints either all make acute angles with the positive  -axis, or all make obtuse angles with the positive
-axis, or all make obtuse angles with the positive  -axis.
-axis. - Let
 , and let
, and let  . PROVE that:
. PROVE that:
 (hence there’s no solution except
(hence there’s no solution except  )
) .
.
- Let
 as before.
as before.
- If
 , PROVE that
, PROVE that 
- Under the above condition, deduce that
 , or
, or  , where
, where  is the golden ratio.
is the golden ratio.
- If
- Let
 as before.
as before.
- If
 , PROVE that
, PROVE that 
- Under the above condition, deduce that
 , or
, or  , where
, where  is the golden ratio.
is the golden ratio.
- If