Take vertex ![]() of triangle
of triangle ![]() , together with the orthocenter
, together with the orthocenter ![]() of the triangle, and our new point
of the triangle, and our new point ![]() with coordinates
with coordinates
(1) 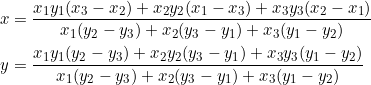
then the resulting triangle ![]() has the following property: the slopes of its sides form a geometric progression. Same with vertices
has the following property: the slopes of its sides form a geometric progression. Same with vertices ![]() and
and ![]() as well as the corresponding triangles
as well as the corresponding triangles ![]() and
and ![]() (examples 6 and 10). This construction works for all triangles, except those triangles with one side parallel to the
(examples 6 and 10). This construction works for all triangles, except those triangles with one side parallel to the ![]() or
or ![]() axis.
axis.
Rigid transversals
If we draw three line segments from ![]() to each of the three vertices
to each of the three vertices ![]() of any triangle
of any triangle ![]() , then the line segments
, then the line segments ![]() either all make acute angles with the
either all make acute angles with the ![]() -axis or all make obtuse angles with the
-axis or all make obtuse angles with the ![]() -axis. See example 2 below.
-axis. See example 2 below.
In ![]() , let
, let ![]() be the slopes of sides
be the slopes of sides ![]() , respectively. PROVE that the slopes of the line segments
, respectively. PROVE that the slopes of the line segments ![]() are
are ![]() ,
, ![]() ,
, ![]() , in that order.
, in that order.
Let the coordinates of the vertices be ![]() ,
, ![]() , and
, and ![]() . With
. With ![]() as in equation (1), we can calculate the slope of
as in equation (1), we can calculate the slope of ![]() (those of
(those of ![]() and
and ![]() are similar).
are similar).
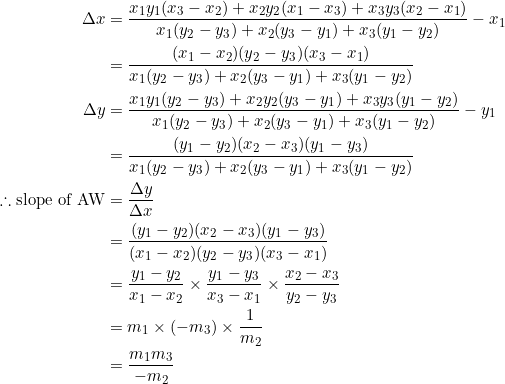
The placement of the negative sign beside ![]() was deliberate: to make it easy to remember the formula for the slope of
was deliberate: to make it easy to remember the formula for the slope of ![]() as well as those of
as well as those of ![]() and
and ![]() . Here’s how it works: the slope of
. Here’s how it works: the slope of ![]() is the product of the slopes of the two sides (
is the product of the slopes of the two sides (![]() and
and ![]() ) that originate from vertex
) that originate from vertex ![]() divided by the negative of the slope of the side opposite vertex
divided by the negative of the slope of the side opposite vertex ![]() (side
(side ![]() ).
).
In any ![]() , PROVE that the line segments
, PROVE that the line segments ![]() either all make acute angles with the positive
either all make acute angles with the positive ![]() -axis or all make obtuse angles with the positive
-axis or all make obtuse angles with the positive ![]() -axis.
-axis.
The slopes from ![]() to
to ![]() are given by:
are given by:
(2) ![]()
Re-write the terms in (2) as
(3) ![]()
and consider four cases:
- Case I:
 are all positive. In this case, the product
are all positive. In this case, the product  is also positive and so each term in equation (3) is negative.
is also positive and so each term in equation (3) is negative. - Case II:
 are all negative. In this case, the product
are all negative. In this case, the product  is also negative and so each term in equation (3) is positive.
is also negative and so each term in equation (3) is positive. - Case III: two of
 are positive while the third is negative; specifically, let
are positive while the third is negative; specifically, let  be positive while
be positive while  is negative. In this case, the product
is negative. In this case, the product  is negative, and so the terms in equation (3) are all positive.
is negative, and so the terms in equation (3) are all positive. - Case IV: one of
 is positive while the other two are negative; specifically, let
is positive while the other two are negative; specifically, let  be positive while
be positive while  and
and  are negative. In this case, the product
are negative. In this case, the product  will be positive and so the terms in equation (3) will be negative.
will be positive and so the terms in equation (3) will be negative.
In ![]() , let
, let ![]() be the slopes of sides
be the slopes of sides ![]() , respectively. PROVE that the line segment
, respectively. PROVE that the line segment ![]() is perpendicular to side
is perpendicular to side ![]() if and only if
if and only if ![]() .
.
![]() can also be perpendicular to
can also be perpendicular to ![]() or
or ![]() , but requiring it to be perpendicular to
, but requiring it to be perpendicular to ![]() is more convenient.
is more convenient.
First suppose that ![]() is perpendicular to
is perpendicular to ![]() . Since the slope of
. Since the slope of ![]() is
is ![]() and the slope of
and the slope of ![]() is
is ![]() , we have:
, we have:
![]()
Conversely, suppose that ![]() . Let’s simplify the slope of
. Let’s simplify the slope of ![]() :
:
![]()
This shows that ![]() is perpendicular to
is perpendicular to ![]() .
.
(The case where ![]() and
and ![]() is a special case. The case where
is a special case. The case where ![]() and
and ![]() is an extremely pleasant case.)
is an extremely pleasant case.)
In ![]() , let
, let ![]() be the slopes of sides
be the slopes of sides ![]() , respectively. PROVE that
, respectively. PROVE that ![]() is parallel to
is parallel to ![]() if and only if
if and only if ![]() (in other words, the slopes of sides
(in other words, the slopes of sides ![]() and
and ![]() are negatives of each other).
are negatives of each other).
First suppose that ![]() is parallel to
is parallel to ![]() . Set their slopes equal:
. Set their slopes equal:
![]()
However, since we can’t have ![]() in a triangle, we take
in a triangle, we take ![]() .
.
Conversely, suppose that ![]() and re-calculate the slopes of
and re-calculate the slopes of ![]() and
and ![]() :
:
![]()
What this means is that ![]() and
and ![]() are parallel to side
are parallel to side ![]() (in fact,
(in fact, ![]() is the midpoint of
is the midpoint of ![]() under this condition).
under this condition).
Let ![]() be the orthocenter of
be the orthocenter of ![]() , and let
, and let ![]() be the point with coordinates in equation (1). PROVE that the slope of
be the point with coordinates in equation (1). PROVE that the slope of ![]() is the negative reciprocal of the product of the slopes of sides
is the negative reciprocal of the product of the slopes of sides ![]() .
.
If ![]() has vertices at
has vertices at ![]() ,
, ![]() ,
, ![]() , then the coordinates of its orthocenter are given by:
, then the coordinates of its orthocenter are given by:
(4) 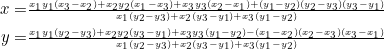
These are very much the same as the coordinates of point ![]() , except for the extra term
, except for the extra term ![]() in the numerator of the
in the numerator of the ![]() -coordinate and the extra term
-coordinate and the extra term ![]() in the
in the ![]() -coordinate. It follows that the slope of the line segment
-coordinate. It follows that the slope of the line segment ![]() is:
is:
(5) ![]()
where ![]() are the slopes of sides
are the slopes of sides ![]() .
.
(Main goal)
For any triangle ![]() with non-zero side-slopes, PROVE that the three triangles
with non-zero side-slopes, PROVE that the three triangles ![]() ,
, ![]() , and
, and ![]() have their side-slopes in geometric progressions.
have their side-slopes in geometric progressions.
We do this for triangle ![]() . The same argument can be adapted for the other two triangles.
. The same argument can be adapted for the other two triangles.
Let the slopes of sides ![]() be
be ![]() . Assume all non-zero.
. Assume all non-zero.
The slope from vertex ![]() to the orthocenter
to the orthocenter ![]() is
is ![]() (by the definition of the altitude from vertex
(by the definition of the altitude from vertex ![]() ). The slope of the line segment
). The slope of the line segment ![]() is
is ![]() (by example 1), and the slope of the line segment
(by example 1), and the slope of the line segment ![]() is
is ![]() (by example 5). Since
(by example 5). Since
![]()
the slopes of sides ![]() form a geometric progression.
form a geometric progression.
Right triangles
In ![]() , let
, let ![]() . PROVE that the slope of
. PROVE that the slope of ![]() is the reciprocal of the slope of the hypotenuse
is the reciprocal of the slope of the hypotenuse ![]() .
.
Let ![]() be the slopes of sides
be the slopes of sides ![]() . By example 1, the slope of the line segment
. By example 1, the slope of the line segment ![]() is
is ![]() . Since the given triangle is right-angled at
. Since the given triangle is right-angled at ![]() , sides
, sides ![]() and
and ![]() are perpendicular, and so
are perpendicular, and so ![]() , which in turn simplifies the slope of the line segment
, which in turn simplifies the slope of the line segment ![]() :
:
![]()
Alternatively, one can also deduce this from example 5.
(The three triangles ![]() reduces to only two for a right triangle, since its orthocenter coincides with a vertex. But we do get a special quadrilateral.)
reduces to only two for a right triangle, since its orthocenter coincides with a vertex. But we do get a special quadrilateral.)
Related trapezium
Let ![]() be a right triangle in which the hypotenuse has slope
be a right triangle in which the hypotenuse has slope ![]() and the legs are not parallel to the coordinate axes. PROVE that the quadrilateral
and the legs are not parallel to the coordinate axes. PROVE that the quadrilateral ![]() is a trapezium.
is a trapezium.
Excluding the case where the legs are parallel to the coordinate axes is essential; if not, ![]() coincides with the orthocenter, which is one of the vertices of a right triangle.
coincides with the orthocenter, which is one of the vertices of a right triangle.
Suppose we have ![]() and
and ![]() . According to example 7, the slope of
. According to example 7, the slope of ![]() will be
will be ![]() as well, meaning that
as well, meaning that ![]() is parallel to
is parallel to ![]() . This gives the required trapezium
. This gives the required trapezium ![]() . Similarly, if the slope of the hypotenuse
. Similarly, if the slope of the hypotenuse ![]() is
is ![]() (that is
(that is ![]() ), then the slope of
), then the slope of ![]() is again
is again ![]() , and this gives a trapezium
, and this gives a trapezium ![]() .
.
(Note that the slopes of ![]() and
and ![]() are reciprocals of each other under the above condition. Together with the slope of
are reciprocals of each other under the above condition. Together with the slope of ![]() as
as ![]() , we get that the slopes of the line segments
, we get that the slopes of the line segments ![]() form a geometric progression, even though the slopes of the sides of the parent triangle
form a geometric progression, even though the slopes of the sides of the parent triangle ![]() do not form a geometric progression.)
do not form a geometric progression.)
Calculate the coordinates of point ![]() for
for ![]() with vertices at
with vertices at ![]() ,
, ![]() ,
, ![]() . Deduce that
. Deduce that ![]() is a trapezium.
is a trapezium.
Observe that ![]() is right-angled at
is right-angled at ![]() . Using equation (1) with
. Using equation (1) with ![]() ,
, ![]() , and
, and ![]() , we get:
, we get:
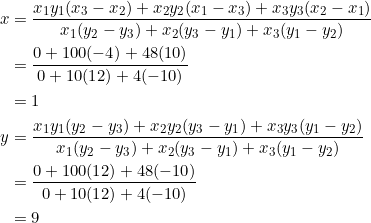
Thus, ![]() is located at
is located at ![]() in the Cartesian plane. The slope of
in the Cartesian plane. The slope of ![]() is
is ![]() , and the slope of
, and the slope of ![]() is
is ![]() , so the two line segments are parallel. The slope of
, so the two line segments are parallel. The slope of ![]() is
is ![]() , while the slope of
, while the slope of ![]() is
is ![]() . Therefore, we obtain a trapezium.
. Therefore, we obtain a trapezium.
(Notice that the slopes of ![]() form a geometric progression, despite the fact the the slopes of the parent triangle
form a geometric progression, despite the fact the the slopes of the parent triangle ![]() do not form a geometric progression.)
do not form a geometric progression.)
Calculate the coordinates of ![]() for
for ![]() with vertices at
with vertices at ![]() ,
, ![]() , and
, and ![]() . Deduce that
. Deduce that ![]() is a trapezium. Verify also that the slopes of the sides of triangles
is a trapezium. Verify also that the slopes of the sides of triangles ![]() ,
, ![]() , and
, and ![]() form geometric progressions.
form geometric progressions.
Unlike in the preceding example, the given triangle ![]() is not right-angled this time. So this example is saying that we can still obtain this special trapezium even when the starting triangle is not right-angled. Using equation (1) with
is not right-angled this time. So this example is saying that we can still obtain this special trapezium even when the starting triangle is not right-angled. Using equation (1) with ![]() ,
, ![]() , and
, and ![]() , we get:
, we get:
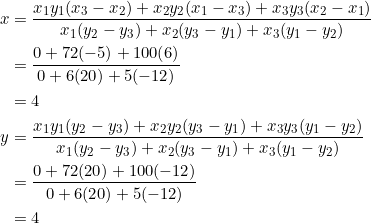
Thus, ![]() is the point
is the point ![]() . With this, the slope of
. With this, the slope of ![]() is
is ![]() . Since the slope of
. Since the slope of ![]() is also
is also ![]() , it follows that
, it follows that ![]() is parallel to
is parallel to ![]() . The slope of
. The slope of ![]() is
is ![]() and the slope of
and the slope of ![]() is
is ![]() . So we obtain a trapezium
. So we obtain a trapezium ![]() .
.
Behind the scences, we calculated the orthocenter of triangle ![]() ; it is the point
; it is the point ![]() . Together with
. Together with ![]() and the given vertices
and the given vertices ![]() ,
, ![]() ,
, ![]() , we have the following slopes:
, we have the following slopes:
![]()
The slopes of the sides of ![]() are then
are then ![]() ; the slopes of the sides of
; the slopes of the sides of ![]() are
are ![]() ; the slopes of the sides of
; the slopes of the sides of ![]() are
are ![]() . These form geometric progressions with common ratios
. These form geometric progressions with common ratios ![]() , respectively.
, respectively.
(Notice that the slopes of ![]() form a geometric progression, despite the fact the the slopes of the parent triangle
form a geometric progression, despite the fact the the slopes of the parent triangle ![]() do not form a geometric progression.)
do not form a geometric progression.)
Takeaway
Let ![]() be the point on the nine-point circle of
be the point on the nine-point circle of ![]() whose coordinates were given in equation (1). Let
whose coordinates were given in equation (1). Let ![]() be the orthocenter of
be the orthocenter of ![]() . Then the following statements are equivalent:
. Then the following statements are equivalent:
- the slopes of sides
 and
and  are reciprocals of each other
are reciprocals of each other - the line segment
 is perpendicular to side
is perpendicular to side 
 is the midpoint of the line segment
is the midpoint of the line segment  .
.
You’ll be getting used to equivalent statements by now.
Tasks
- For
 with vertices at
with vertices at  ,
,  ,
,  , calculate the slopes of line segments
, calculate the slopes of line segments  ,
,  , and
, and  . Verify that
. Verify that  is perpendicular to
is perpendicular to  .
. - Let
 be such that side
be such that side  is parallel to the
is parallel to the  -axis. PROVE that:
-axis. PROVE that:
 coincides with the foot of the altitude from vertex
coincides with the foot of the altitude from vertex 
- none of the triangles
 has slopes in geometric progression.
has slopes in geometric progression.
(This is the only exception to the main point in today’s discussion.)
- In
 , let
, let  be as given in equation (1). PROVE that the slopes of
be as given in equation (1). PROVE that the slopes of  and
and  are reciprocals of each other if and only if the slope of side
are reciprocals of each other if and only if the slope of side  is
is 
- PROVE if the slopes of the sides of a triangle form a geometric progression with common ratio
 , then the slopes of
, then the slopes of  form a geometric progression with common ratio
form a geometric progression with common ratio  .
. - In
 , let
, let  be the slopes of sides
be the slopes of sides  . PROVE that the following statements are equivalent:
. PROVE that the following statements are equivalent:
 is parallel to
is parallel to 

(Under this condition, the slopes of line segments form a geometric progression.)
form a geometric progression.)