Let ![]() be the nine-point center of triangle
be the nine-point center of triangle ![]() . We showed in our previous post that if the parent triangle is right-angled with
. We showed in our previous post that if the parent triangle is right-angled with ![]() , then
, then
(1) ![]()
We’ll now prove what holds more generally for any triangle:
(2) ![]()
![]() being the circumradius and
being the circumradius and ![]() the usual side-lengths.
the usual side-lengths.
Memory recall
Let’s first be reminded of the main ingredient: Stewart’s theorem. It states that given a triangle ![]() with side-lengths
with side-lengths ![]() and a cevian
and a cevian ![]() like the one depicted below:
like the one depicted below:
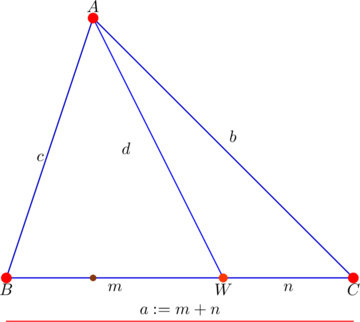
(3) ![]()
Main results
In ![]() with the usual notation, PROVE that the orthocenter-circumcenter distance
with the usual notation, PROVE that the orthocenter-circumcenter distance ![]() satisfies
satisfies ![]() .
.
It was from this amazing site that we first learnt of the above identity. We’ll add our own proof of it to an already existing pool of proofs, using Stewart’s theorem as a tool. We’ll also use the formula for median lengths, and the fact that the centroid divides a median in the ratio ![]() (measured from a vertex) and also divides the Euler line
(measured from a vertex) and also divides the Euler line ![]() in the ratio
in the ratio ![]() (measured from the orthocenter).
(measured from the orthocenter).
Consider the diagram below where ![]() is the centriod of
is the centriod of ![]() ,
, ![]() is the midpoint of
is the midpoint of ![]() , and
, and ![]() (circumradius):
(circumradius):
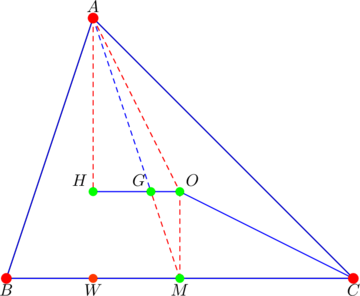
Notice our new point ![]() just
just ![]() andering along side
andering along side ![]() . More importantly, observe that
. More importantly, observe that ![]() is perpendicular to
is perpendicular to ![]() (
(![]() is the midpoint of
is the midpoint of ![]() and
and ![]() is the circumcenter). Therefore, the Pythagorean theorem applied to
is the circumcenter). Therefore, the Pythagorean theorem applied to ![]() gives:
gives:
(4) 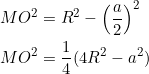
Since ![]() and
and ![]() , Stewart’s theorem applied to
, Stewart’s theorem applied to ![]() gives:
gives:
(5) 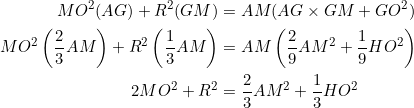
The length of median ![]() satisfies
satisfies ![]() . Thus, combining equations (4) and (5) gives:
. Thus, combining equations (4) and (5) gives:
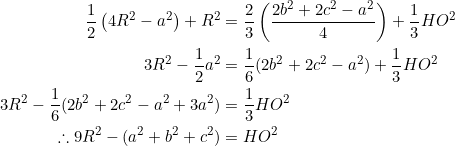
The above procedure works regardless of the vertex we started with. And it also works even in the peculiar case where ![]() are co-linear. It also doesn’t matter if both
are co-linear. It also doesn’t matter if both ![]() and
and ![]() are outside the parent triangle.
are outside the parent triangle.
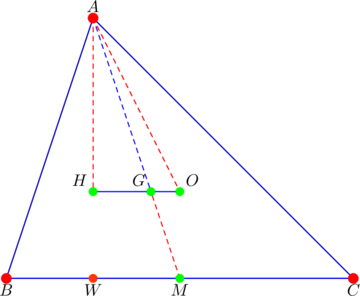
Let ![]() be the orthocenter of
be the orthocenter of ![]() with circum-radius
with circum-radius ![]() . PROVE that
. PROVE that ![]() .
.
Apply Stewart’s theorem to ![]() in the diagram below:
in the diagram below:
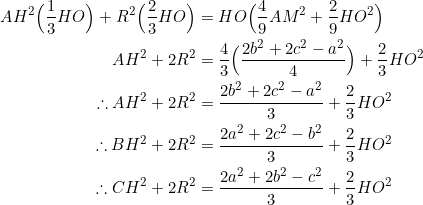
Add all the three last equations:
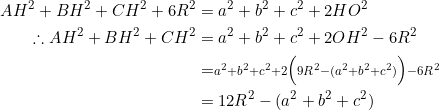
Let ![]() and
and ![]() be the nine-point center and orthocenter of
be the nine-point center and orthocenter of ![]() . PROVE that
. PROVE that ![]() .
.
We only slightly modify the proof given in example 2, replacing the centroid with the nine-point center ![]() (note that
(note that ![]() is the midpoint of
is the midpoint of ![]() ).
).
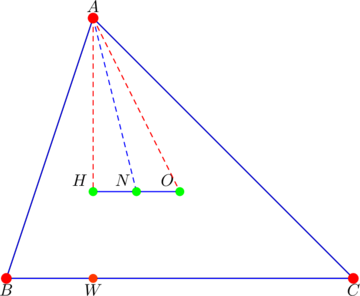
In ![]() above,
above, ![]() is a median, so:
is a median, so:
![]()
Similarly, if we connect the segment ![]() to vertices
to vertices ![]() and
and ![]() instead, we obtain (with
instead, we obtain (with ![]() and
and ![]() as medians)
as medians)
![]()
Add the expressions for ![]() and simplify:
and simplify:
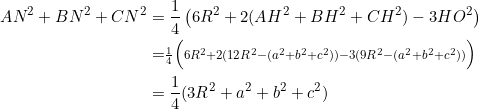
Since ![]() , we have
, we have ![]() . In turn:
. In turn:
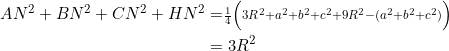
PROVE that ![]() , where
, where ![]() is the nine-point center of
is the nine-point center of ![]() . Hence deduce that in a right triangle
. Hence deduce that in a right triangle ![]() with hypotenuse of length
with hypotenuse of length ![]() , the sum of the squares of the distances from the vertices to the nine-point center is
, the sum of the squares of the distances from the vertices to the nine-point center is ![]() the length of the hypotenuse.
the length of the hypotenuse.
We obtained ![]() as an intermediate step in example 3 above.
as an intermediate step in example 3 above.
Now if ![]() is such that
is such that ![]() is the hypotenuse with length
is the hypotenuse with length ![]() , then
, then ![]() . The circumradius
. The circumradius ![]() is half of the length of the hypotenuse, so
is half of the length of the hypotenuse, so ![]() . Substituting in the expression for
. Substituting in the expression for ![]() , we obtain:
, we obtain:
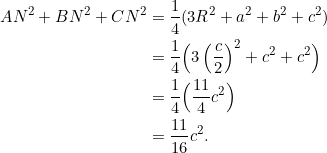
We show in example 5 below that the above relation also holds in a non-right triangle setting.
Consider ![]() in which
in which ![]() and
and ![]() . PROVE that
. PROVE that ![]() .
.
(If you’re curious as to how we obtained ![]() , see example 7 for a sample procedure.)
, see example 7 for a sample procedure.)
A key ingredient in the proof is the fact that the circumradius ![]() can be expressed as
can be expressed as ![]() as per the extended law of sines.
as per the extended law of sines.
Since ![]() , the cosine law gives
, the cosine law gives
![]()
Also:
![]()
Equation (2) becomes:
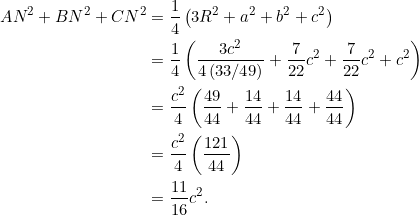
Show that the circumradius ![]() of an equilateral triangle
of an equilateral triangle ![]() can be given by
can be given by ![]() , where
, where ![]() is the length of one of the sides.
is the length of one of the sides.
The orthocenter and circumcenter coincide for an equilateral triangle, so the distance ![]() . Using example 1 and
. Using example 1 and ![]() , we have:
, we have:
![]()
In ![]() , suppose that
, suppose that ![]() . PROVE that either
. PROVE that either ![]() or
or ![]() . If one has
. If one has ![]() in addition, deduce that the triangle is equilateral.
in addition, deduce that the triangle is equilateral.
One can easily check that if a right triangle satisfies ![]() , then
, then ![]() . So the above example is basically saying that the equation
. So the above example is basically saying that the equation ![]() is not exclusive to right triangles.
is not exclusive to right triangles.
From example 2: ![]() . Set the left side equal to
. Set the left side equal to ![]() :
:
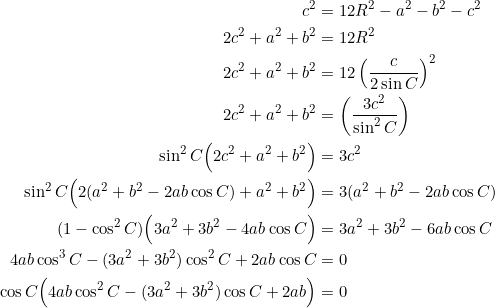
Thus, either ![]() (giving a right triangle), or
(giving a right triangle), or
![]()
as required. Now let ![]() , then:
, then:
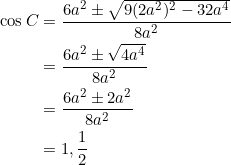
If ![]() , then
, then ![]() , which is not allowed for a normal non-degenerate triangle. Therefore we must take
, which is not allowed for a normal non-degenerate triangle. Therefore we must take ![]() , which yields
, which yields ![]() . Since we already assumed that
. Since we already assumed that ![]() , it follows that we obtain an equilateral triangle.
, it follows that we obtain an equilateral triangle.
Mere repetitions
What follows are particular cases of some of the preceding examples, applied to our new point ![]() whose coordinates are given by:
whose coordinates are given by:
(6) 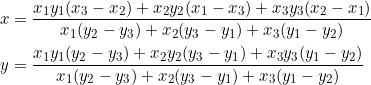
Let ![]() be the nine-point center of
be the nine-point center of ![]() and let
and let ![]() be the point given in equation (6). PROVE that
be the point given in equation (6). PROVE that ![]() , if
, if ![]() has two sides parallel to the coordinate axes.
has two sides parallel to the coordinate axes.
Trivial stuff. If ![]() has legs parallel to the coordinate axes, then
has legs parallel to the coordinate axes, then ![]() , based on one of the equivalent conditions in our previous post. The conclusion now follows from example 3.
, based on one of the equivalent conditions in our previous post. The conclusion now follows from example 3.
If ![]() has two sides parallel to the coordinate axes, PROVE that
has two sides parallel to the coordinate axes, PROVE that ![]() , where
, where ![]() is the point given by equation (6).
is the point given by equation (6).
Trivial stuff, twice. Under the given condition, we have ![]() . Thus, the conclusion follows from example 2 above.
. Thus, the conclusion follows from example 2 above.
Let ![]() be such that two sides have slopes
be such that two sides have slopes ![]() . PROVE that
. PROVE that ![]() , where
, where ![]() is the point with coordinates given by equation (6).
is the point with coordinates given by equation (6).
Trivial stuff, thrice. The given triangle is obviously a right triangle. Since the legs have slopes ![]() , point
, point ![]() coincides with the circumcenter. Therefore we have
coincides with the circumcenter. Therefore we have ![]() by example 1 above.
by example 1 above.
Takeaway
Let ![]() be the side-lengths of
be the side-lengths of ![]() , and let
, and let ![]() be the orthocenter, circumcenter, and nine-point center, respectively.
be the orthocenter, circumcenter, and nine-point center, respectively.
The following statements are equivalent:

 or
or 
The following statements are also equivalent:

 or
or 
And the following two statements too are equivalent:

 or
or 
Bottom line: Many non-right triangles share properties (relating to ![]() and stuff) that one would have thought to be exclusive to the right triangle.
and stuff) that one would have thought to be exclusive to the right triangle.
Tasks
- Let
 be the centroid of
be the centroid of  , and let
, and let  be the circumcenter.
be the circumcenter.
- PROVE that
 , where
, where  are the usual side-lengths.
are the usual side-lengths. - Deduce that
 .
.
- PROVE that
- Let
 and
and  be the orthocenter and nine-point center of
be the orthocenter and nine-point center of  . PROVE that
. PROVE that  .
. - Let
 be the orthocenter, circumcenter and nine-point center of
be the orthocenter, circumcenter and nine-point center of  . PROVE that:
. PROVE that:

 .
.
- Let
 be the orthocenter of
be the orthocenter of  with circumradius
with circumradius  and side-lengths
and side-lengths  .
.
- PROVE that

- Deduce that the distance from vertex
 to the orthocenter is twice the distance from the circumcenter to the midpoint of side
to the orthocenter is twice the distance from the circumcenter to the midpoint of side  .
.
- PROVE that
- This exercise shows that there are many non-right triangles with the property that the length of the Euler line
 is half of the length of a side of the triangle. Suppose that in
is half of the length of a side of the triangle. Suppose that in  one has
one has  . PROVE that:
. PROVE that:
 or
or 
- if
 in addition, then
in addition, then  . (Thus, any isosceles triangle in which
. (Thus, any isosceles triangle in which  and
and  will satisfy
will satisfy  . And it’s even possible to realize this with a non-right, scalene triangle.)
. And it’s even possible to realize this with a non-right, scalene triangle.)
- Consider
 with vertices at
with vertices at  ,
,  ,
,  . Verify that:
. Verify that:
- the orthocenter is
 and the circumcenter is
and the circumcenter is 

- the orthocenter is
- Find coordinates for the vertices of a non-right triangle
 with orthocenter
with orthocenter  and side-lengths
and side-lengths  such that
such that  .
. - Find coordinates for the vertices of a non-right triangle
 with nine-point center
with nine-point center  and side-lengths
and side-lengths  such that
such that  .
. - Consider a quadrilateral
 with vertices at
with vertices at  ,
,  ,
,  ,
,  . PROVE that:
. PROVE that:
- sides
 and
and  have opposite slopes, and their lengths are in the ratio
have opposite slopes, and their lengths are in the ratio 
- sides
 and
and  have opposite slopes, and their lengths are in the ratio
have opposite slopes, and their lengths are in the ratio 
- diagonals
 and
and  have opposite slopes, and their lengths are in the ratio
have opposite slopes, and their lengths are in the ratio 
- the longer diagonal
 bisects the shorter diagonal
bisects the shorter diagonal 
- the shorter diagonal
 divides the longer diagonal
divides the longer diagonal  in the ratio
in the ratio 
 is a cyclic quadrilateral.
is a cyclic quadrilateral.
(The point that partly facilitated these features is among the quartet of points we’ll introduce later this year, if time/space permits.)
that partly facilitated these features is among the quartet of points we’ll introduce later this year, if time/space permits.)
- sides
- Consider
 with vertices at
with vertices at  ,
,  ,
,  ,
,  . PROVE that
. PROVE that  , where
, where  is the length of the median from vertex
is the length of the median from vertex  .
.