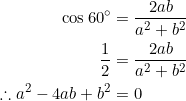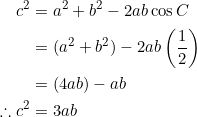(1) ![]()
then the following statements are equivalent:
 is the golden ratio
is the golden ratio



Today’s post will now establish the above equivalence. (Note that the fourth condition, ![]() , which motivated today’s title, was coined by the author of this article.)
, which motivated today’s title, was coined by the author of this article.)
Suppose that ![]() is the golden ratio, then
is the golden ratio, then ![]() , and so
, and so ![]() . This then gives
. This then gives ![]() . In turn:
. In turn:
![]()
Let ![]() be the circumradius. Then, by the extended law of sines, we have:
be the circumradius. Then, by the extended law of sines, we have:
![]()
The assumption ![]() implies
implies ![]() . (Henceforth we’ll frequently use the fact that
. (Henceforth we’ll frequently use the fact that ![]() is equivalent to equation (1).) So:
is equivalent to equation (1).) So:
![]()
Using the extended law of sines as in the previous example, the condition ![]() gives
gives ![]() . Since
. Since ![]() , we obtain
, we obtain
![]()
So-called upside-down Pythagorean identity. Ours works under an added condition, namely equation (1).
Re-arrange the given condition ![]() as
as
![]()
and obtain ![]() . The length of the altitude from vertex
. The length of the altitude from vertex ![]() is given by
is given by
![]()
If ![]() , then
, then ![]() . Now use this in equation (1) to get
. Now use this in equation (1) to get
![]()
Thus, ![]() is the golden ratio.
is the golden ratio.
Takeaway
Let ![]() be a triangle whose side-lengths
be a triangle whose side-lengths ![]() satisfy equation (1). Then the following statements are equivalent:
satisfy equation (1). Then the following statements are equivalent:
 is the golden ratio
is the golden ratio
 .
.
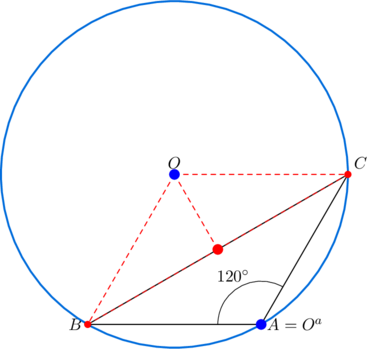
The last condition fixes the interior angles of the given triangle ![]() :
: ![]() ,
, ![]() ,
, ![]() .
.
Task
- (Early sixties) In a non-right triangle
 , let
, let  be the side-lengths,
be the side-lengths,  the altitudes,
the altitudes,  the feet of the altitudes from the respective vertices,
the feet of the altitudes from the respective vertices,  the circumradius,
the circumradius,  the circumcenter,
the circumcenter,  the nine-point center,
the nine-point center,  the orthocenter,
the orthocenter,  the midpoint of side
the midpoint of side  ,
,  the reflection of
the reflection of  over side
over side  ,
,  the reflection of
the reflection of  over side
over side  , and
, and  the reflection of
the reflection of  over side
over side  . PROVE that the following sixty-one statements are equivalent:
. PROVE that the following sixty-one statements are equivalent:































 or
or 




 is congruent to
is congruent to 
 is congruent to
is congruent to 
 is isosceles with
is isosceles with 
 is isosceles with
is isosceles with 
 is right angled at
is right angled at 
 is the circumcenter of
is the circumcenter of 
 is right-angled at
is right-angled at 
 is right-angled at
is right-angled at 
- quadrilateral
 is a rectangle
is a rectangle - the points
 are concyclic with
are concyclic with  as diameter
as diameter - the reflection
 of
of  over
over  lies internally on
lies internally on 
- the reflection
 of
of  over
over  lies externally on
lies externally on 
- radius
 is parallel to side
is parallel to side 
 is the reflection of
is the reflection of  over side
over side 
- the nine-point center lies on

- the orthic triangle is isosceles with

- the geometric mean theorem holds
- the bisector of
 has length
has length  , where
, where 
- the orthocenter is a reflection of vertex
 over side
over side 
- segment
 is tangent to the circumcircle at point
is tangent to the circumcircle at point 
- median
 has the same length as the segment
has the same length as the segment 
- the bisector
 of
of  is tangent to the nine-point circle at
is tangent to the nine-point circle at 
 is a convex kite with diagonals
is a convex kite with diagonals  and
and 
- altitude
 is tangent to the nine-point circle at
is tangent to the nine-point circle at 
- segment
 is tangent to the nine-point circle at
is tangent to the nine-point circle at  .
.
( short of the target.)
short of the target.)
- (Extra feature) If
 satisfies equation (??), PROVE that its nine-point center
satisfies equation (??), PROVE that its nine-point center  divides
divides  in the ratio
in the ratio  .
.