Writing for the third time on the geometric mean theorem, after an external eye scrutinized and stamped the previous two writings on the same theme, seems a joy thing.
With that said, today’s post focuses on numerical problems that concretize the geometric mean theorem in obtuse triangles.
Wow! Thanks for clicking.
Note that the triangle in this first example is a 30-30-120 triangle; it satisfies the geometric mean theorem twice.

From the above diagram, ![]() . Also
. Also ![]() and
and ![]() . Thus:
. Thus:
![]()
Similarly, if ![]() denotes the foot of the altitude from vertex
denotes the foot of the altitude from vertex ![]() , then:
, then:
![]()
Another unique property of the ![]() triangle.
triangle.

From the above diagram, ![]() . And so:
. And so:
![]()
In words: the altitude ![]() is the geometric mean of the segments
is the geometric mean of the segments ![]() and
and ![]() .
.

From the above diagram, ![]() . And so:
. And so:
![]()
In words: the altitude ![]() is the geometric mean of the segments
is the geometric mean of the segments ![]() and
and ![]() .
.

From the above diagram, ![]() . And so:
. And so:
![]()
In words: the altitude ![]() is the geometric mean of the segments
is the geometric mean of the segments ![]() and
and ![]() .
.
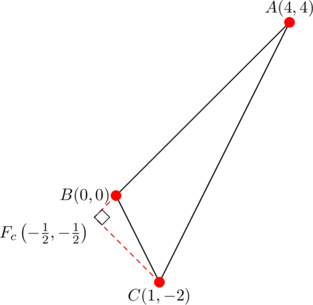
From the above diagram, ![]() . And so:
. And so:
![]()
In words: the altitude ![]() is the geometric mean of the segments
is the geometric mean of the segments ![]() and
and ![]() .
.
Takeaway
The two statements below, the geometric mean theorem, and (more than) 75 other statements, are equivalent in any non-right triangle with circumradius ![]() and side-lenths
and side-lenths ![]() :
:

 .
.
Task
- (Aufbau) In triangle
 , let
, let  be the side-lengths,
be the side-lengths,  the circumradius,
the circumradius,  the circumcenter,
the circumcenter,  the nine-point center, and
the nine-point center, and  the orthocenter. PROVE that the following statements are equivalent:
the orthocenter. PROVE that the following statements are equivalent:



- the reflection of
 over
over  is
is 
- the circle with diameter
 passes through vertices
passes through vertices  and
and 
- radius
 is parallel to side
is parallel to side  and radius
and radius  is parallel to side
is parallel to side 
- the reflection of
 over
over  is
is  and the reflection of
and the reflection of  over
over  is
is 
 is the geometric mean of
is the geometric mean of  and
and  , and
, and  is the geometric mean of
is the geometric mean of  and
and  . (
. ( and
and  are the feet of the altitudes from
are the feet of the altitudes from  and
and  , respectively.)
, respectively.)