Nine-point center equals a vertex II

Among all triangles, the only triangle whose nine-point center coincides with one of its vertices is the $30^{\circ}-30^{\circ}-120^{\circ}$ -triangle.

As such, it has unique properties, some of which will be shown in today’s post.

Additionally, the $30^{\circ}-30^{\circ}-120^{\circ}$ -triangle is also unique among all isosceles triangles, and we’ll see that later.

PROVE that in the $30^{\circ}-30^{\circ}-120^{\circ}$

-triangle, the two equal sides are equal to the circumradius.

Let $R$ be the circumradius and let $a,b,c$ be the side-lengths of a given triangle $ABC$ . By the extended law of sines we have:

$R=\frac{a}{2\sin A}=\frac{b}{2\sin B}=\frac{c}{2\sin C}$

In the event that $A=C=30^{\circ}$ , we get $R=a=c$ .

If one vertex of a triangle is equidistant from the midpoints of its sides, PROVE that the triangle is the $30^{\circ}-30^{\circ}-120^{\circ}$

-triangle.

Suppose that vertex $B$ of triangle $ABC$ is equidistant from the midpoints of sides $AB,BC,CA$ . In particular, this means that the median from vertex $B$ is equal to half the side-lengths of $AB$ and $BC$ .

$\begin{equation*} \begin{split} \frac{2a^2+2c^2-b^2}{4}&=\frac{a^2}{4}\\ \implies a^2+2c^2&=b^2\\ \frac{2a^2+2c^2-b^2}{4}&=\frac{c^2}{4}\\ \implies 2a^2+c^2&=b^2\\ \therefore a&=c \end{split} \end{equation*}$

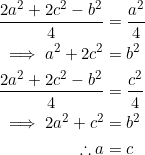
By the cosine formula:

$\cos B=\frac{a^2+c^2-b^2}{2ac}=\frac{a^2+a^2-(a^2+2a^2)}{2a^2}=-\frac{1}{2}\implies B=120^{\circ}$

Consequently, $A=C=30^{\circ}$ .

PROVE that in the $30^{\circ}-30^{\circ}-120^{\circ}$

-triangle, one vertex is equidistant from the midpoints of the three sides.

Note that the side-lengths $a,b,c$ are in the ratio $a:b:c=1:\sqrt{3}:1$ , and so $b^2=3a^2=3c^2$ . Consider the length of the median from vertex $B$ :

$\begin{equation*} \begin{split} m_b^2&=\frac{2a^2+2c^2-b^2}{4}\\ &=\frac{2a^2+2a^2-3a^2}{4}\\ &=\frac{a^2}{4}\\ \therefore m_b&=\frac{a}{2}\\ &=\frac{c}{2} \end{split} \end{equation*}$

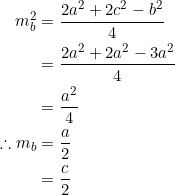
And so vertex $B$ is equidistant from the midpoints of all three sides.

If one vertex of a triangle is equidistant from the feet of its three altitudes, PROVE that the triangle is the $30^{\circ}-30^{\circ}-120^{\circ}$

-triangle.

Let the feet of the altitudes be $F_a,F_b,F_c$ , and let the altitudes themselves be $h_a,h_b,h_c$ . Suppose that vertex $B$ is equidistant from $F_a$ and $F_b$ , that is $BF_a=BF_b$ . Then:

$c^2-h_a^2=h_b^2\implies c^2-\left(\frac{bc}{2R}\right)^2=\left(\frac{ac}{2R}\right)^2\implies a^2+b^2=4R^2$

Similarly, let $BF_b=BF_c$ :

$h_b^2=a^2-h_c^2\implies \left(\frac{ac}{2R}\right)^2=a^2-\left(\frac{ab}{2R}\right)^2\implies b^2+c^2=4R^2$

And so $a=c$ . Since $a^2+b^2=4R^2$ is equivalent to $(b^2-a^2)^2=(ac)^2+(cb)^2$ , we obtain $b^2=3a^2$ . In turn, $B=120^{\circ}$ . The fact that $a=c$ then gives $A=C=30^{\circ}$ .

PROVE that in the $30^{\circ}-30^{\circ}-120^{\circ}$

-triangle, one vertex is equidistant from the feet of all three altitudes.

Easy converse to the preceding example.

Takeaway

In any triangle $ABC$ , let $a,b,c$ be the side-lengths and $R$ the circumradius. Then the following statements are equivalent:

$R=a=c$
$\angle A=\angle C=30^{\circ}$
$B$ is equidistant from the midpoints of the sides
$B$ is equidistant from the feet of the three altitudes
$B$ is equidistant from the three Euler points.

Such $B$ must be the nine-point center.

Task

(Late seventies) In a non-right triangle , let be the side-lengths, the altitudes, the feet of the altitudes from the respective vertices, the midpoints of sides , the Euler points, the circumradius, the circumcenter, the nine-point center, the orthocenter, the reflection of over side , the reflection of over side , and the reflection of over side . PROVE that the following seventy-eight statements are equivalent:
1. $E_c=F_c$
2. $AH=b$
3. $BH=a$
4. $AE_a=\frac{b}{2}$
5. $BE_b=\frac{a}{2}$
6. $E_aM_c=\frac{a}{2}$
7. $E_bM_c=\frac{b}{2}$
8. $E_aM_b=h_c$
9. $E_aF_b=\frac{AH}{2}$
10. $E_bF_a=\frac{BH}{2}$
11. $OO^a=b$
12. $OO^b=a$
13. $CH=2h_c$
14. $h_a=AF_b$
15. $h_b=BF_a$
16. $AF_c=\frac{b^2}{2R}$
17. $BF_c=\frac{a^2}{2R}$
18. $\frac{a}{c} =\frac{h_c}{AF_b}$
19. $\frac{b}{c}=\frac{h_c}{BF_a}$
20. $\frac{a}{b}=\frac{BF_a}{AF_b}$
21. $R=\frac{b^2-a^2}{2c}$
22. $h_c=R\cos C$
23. $\cos A=\frac{b}{\sqrt{a^2+b^2}}$
24. $\cos B=-\frac{a}{\sqrt{a^2+b^2}}$
25. $\cos C=\frac{2ab}{a^2+b^2}$
26. $\sin A=\frac{a}{\sqrt{a^2+b^2}}$
27. $\sin B=\frac{b}{\sqrt{a^2+b^2}}$
28. $\sin C=\frac{b^2-a^2}{a^2+b^2}$
29. $\cos^2 A+\cos^2 B=1$
30. $\sin^2 A+\sin^2 B=1$
31. $a\cos A+b\cos B=0$
32. $\sin A+\cos B=0$
33. $\cos A-\sin B=0$
34. $2\cos A\cos B+\cos C=0$
35. $2\sin A\sin B-\cos C=0$
36. $\cos A\cos B+\sin A\sin B=0$
37. $a\cos A-b\cos B=\sqrt{a^2+b^2}\cos C$
38. $\sin A\sin B=\frac{ab}{b^2-a^2}\sin C$
39. $\sin^2B-\sin^2A=\sin C$
40. $\cos^2A-\cos^2B=\sin C$
41. $OH^2=5R^2-c^2$
42. $h_a^2+h_b^2=AB^2$
43. $\frac{h_a}{a}+\frac{h_b}{b}=\frac{c}{h_c}$
44. $a^2+b^2=4R^2$
45. $\left(c+2AF_c\right)^2=a^2+b^2$ or $\left(c+2BF_c\right)^2=a^2+b^2$
46. $A-B=\pm 90^{\circ}$
47. $(a^2-b^2)^2=(ac)^2+(cb)^2$
48. $AH^2+BH^2+CH^2=8R^2-c^2$
49. $b=2R\cos A$
50. $E_a$ is the reflection of $M_b$ over side $AB$
51. $E_b$ is the reflection of $M_a$ over side $AB$
52. $\triangle ABH$ is congruent to $\triangle ABC$
53. $\triangle OO^aO^b$ is congruent to $\triangle ABC$
54. $\triangle CNO$ is isosceles with $CN=NO$
55. $\triangle CNH$ is isosceles with $CN=NH$
56. $\triangle CHO$ is right angled at $C$
57. $N$ is the circumcenter of $\triangle CHO$
58. $\triangle O^cOC$ is right-angled at $O$
59. $\triangle O^cHC$ is right-angled at $H$
60. quadrilateral $O^cOHC$ is a rectangle
61. the points $O^c,O,C,H$ are concyclic with $OH$ as diameter
62. the reflection $O^b$ of $O$ over $AC$ lies internally on $AB$
63. the reflection $O^a$ of $O$ over $BC$ lies externally on $AB$
64. radius $OC$ is parallel to side $AB$
65. $F_a$ is the reflection of $F_b$ over side $AB$
66. segment $F_aF_b$ is perpendicular to side $AB$
67. the nine-point center lies on $AB$
68. the orthic triangle is isosceles with $F_aF_c=F_bF_c$
69. the geometric mean theorem holds
70. the bisector of $\angle C$ has length $l$ , where $l^2=\frac{2a^2b^2}{a^2+b^2}$
71. the orthocenter is a reflection of vertex $C$ over side $AB$
72. segment $HC$ is tangent to the circumcircle at point $C$
73. median $CM_c$ has the same length as the segment $HM_c$
74. the bisector $M_cO$ of $AB$ is tangent to the nine-point circle at $M_c$
75. $AF_aBF_b$ is a convex kite with diagonals $AB$ and $F_aF_b$
76. altitude $CF_c$ is tangent to the nine-point circle at $F_c$
77. chord $F_cM_c$ is a diameter of the nine-point circle
78. segment $HF_c$ is tangent to the nine-point circle at $F_c$ .
  (Almost losing count with more still lined up.)