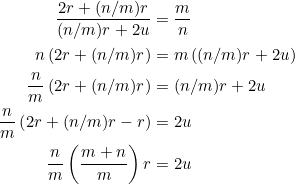We (can always) construct two cevians that concur with a median.
Ratios 1:2, 1:1, 1:2
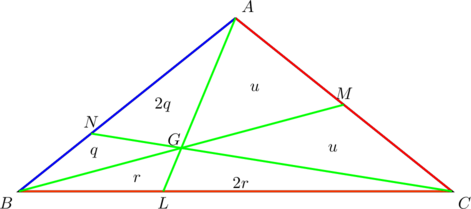
In the diagram below, let cevian ![]() divide side
divide side ![]() such that
such that ![]() ; let
; let ![]() be a median, so that
be a median, so that ![]() ; let cevian
; let cevian ![]() divide side
divide side ![]() in the ratio
in the ratio ![]() .
.
We show that at the point of concurrency, median ![]() is bisected in the ratio
is bisected in the ratio ![]() , while cevians
, while cevians ![]() and
and ![]() are divided in ratios
are divided in ratios ![]() . (Compare this with the manner in which the centroid divides the three medians of a triangle.)
. (Compare this with the manner in which the centroid divides the three medians of a triangle.)
Using the given ratios, PROVE that ![]() are concurrent.
are concurrent.
Just like proving that the three medians of a triangle are concurrent, this question belongs at the simplest level of simplicity. We have:
By the converse of Ceva’s theorem, we conclude that ![]() are concurrent.
are concurrent.
In the diagram below, the small letters ![]() represent the areas of the triangles in which they are located. PROVE that
represent the areas of the triangles in which they are located. PROVE that ![]() , given that
, given that ![]() ,
, ![]() ,
, ![]() .
.
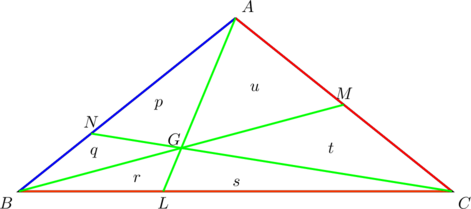
Let’s do this in four steps:
- First, we have
 . Consider
. Consider  and
and  . They have the same altitudes, measured from their common vertex
. They have the same altitudes, measured from their common vertex  . Since their base lengths
. Since their base lengths  and
and  are also equal, their areas must be equal as well. This gives
are also equal, their areas must be equal as well. This gives  .
. - Next we have
 and
and  . Consider
. Consider  and
and  . They have the same altitudes, measured from their common vertex
. They have the same altitudes, measured from their common vertex  . Since
. Since  , the area of
, the area of  is twice that of
is twice that of  so
so  . For the same reason we have
. For the same reason we have  , when
, when  and
and  are compared.
are compared.
Our diagram simplifies to:
- We now show that
 . Consider
. Consider  and
and  . They have the same altitudes, measured from their common vertex
. They have the same altitudes, measured from their common vertex  . Since
. Since  , these two triangles have the same areas, so
, these two triangles have the same areas, so  . This gives
. This gives  .
. - Lastly, we show that
 . Consider
. Consider  and
and  . They have the same altitudes, measured from their common vertex
. They have the same altitudes, measured from their common vertex  . Since
. Since  , the area of
, the area of  is twice the area of
is twice the area of  . Thus,
. Thus,  , and so
, and so  . Since
. Since  from the previous step, we get
from the previous step, we get  as desired.
as desired.
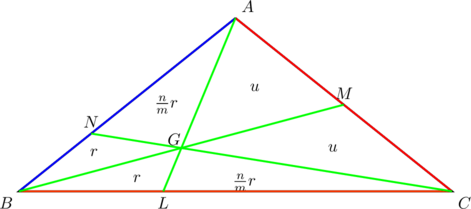
Suppose that ![]() ,
, ![]() , and
, and ![]() in the diagram below:
in the diagram below:
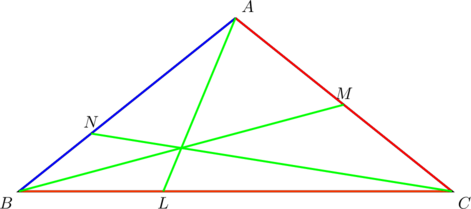
PROVE that at the point of concurrency, ![]() is bisected in the ratio
is bisected in the ratio ![]() ,
, ![]() is divided in the ratio
is divided in the ratio ![]() and
and ![]() is divided in the ratio
is divided in the ratio ![]() .
.
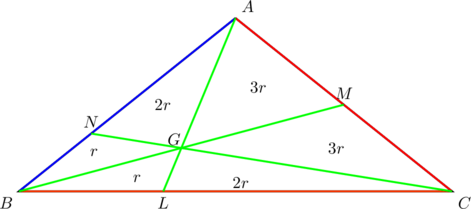
Let the point of concurrency be ![]() and let the area of
and let the area of ![]() be denoted by
be denoted by ![]() . Then, in view of the previous example, the simplified area diagram, in terms of
. Then, in view of the previous example, the simplified area diagram, in terms of ![]() , is:
, is:
Consider ![]() and
and ![]() . They have the same areas, namely
. They have the same areas, namely ![]() . Since they also have the same altitudes (measured from their common vertex
. Since they also have the same altitudes (measured from their common vertex ![]() ), it must be the case that their base lengths are also equal. Thus
), it must be the case that their base lengths are also equal. Thus ![]() .
.
Now consider ![]() and
and ![]() . They have the same altitudes, measured from their common vertex
. They have the same altitudes, measured from their common vertex ![]() . The area of
. The area of ![]() is
is ![]() , while the area of
, while the area of ![]() is
is ![]() . Thus their base lengths
. Thus their base lengths ![]() and
and ![]() must be in the ratio of their areas, so
must be in the ratio of their areas, so ![]() .
.
Similarly we have ![]() .
.
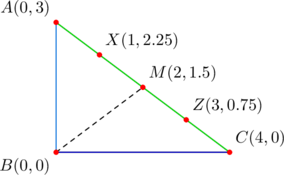
![]() has vertices at
has vertices at ![]() ,
, ![]() , and
, and ![]() . Cevians
. Cevians ![]() divide sides
divide sides ![]() in the ratios
in the ratios ![]() , respectively. Determine the coordinates of the point of concurrency.
, respectively. Determine the coordinates of the point of concurrency.
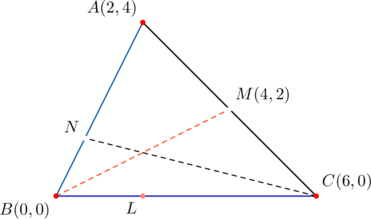
Note that cevian ![]() is a median. So it is bisected
is a median. So it is bisected ![]() at the point of concurrency, in view of the given ratios. This means that the midpoint of
at the point of concurrency, in view of the given ratios. This means that the midpoint of ![]() is the point of concurrency. Since
is the point of concurrency. Since ![]() is the midpoint of
is the midpoint of ![]() , it is the point
, it is the point ![]() . Then we take the midpoint of
. Then we take the midpoint of ![]() and
and ![]() to get
to get ![]() as the point of concurrency.
as the point of concurrency.
- Since
 divides
divides  in the ratio
in the ratio  , it is the point
, it is the point  . Then the point of concurrency divides
. Then the point of concurrency divides  in the ratio
in the ratio  , measured from vertex
, measured from vertex  . So it is the point
. So it is the point  , as before.
, as before. - Since
 divides
divides  in the ratio
in the ratio  , it is the point
, it is the point  . The point of concurrency divides cevian
. The point of concurrency divides cevian  in the ratio
in the ratio  , measured from
, measured from  . So it is the point
. So it is the point  , as before.
, as before.
So we obtain the same point ![]() , but the last two approaches involved more steps.
, but the last two approaches involved more steps.
Ratios m:n, 1:1, m:n
This is a slight generalization of the previous examples.
In the diagram below, the small letters ![]() represent the areas of the triangles in which they are located. PROVE that
represent the areas of the triangles in which they are located. PROVE that ![]() , given that
, given that ![]() ,
, ![]() ,
, ![]() .
.

As before, we do this in steps:
- First we have
 , because
, because  and both
and both  and
and  have the same height.
have the same height. - Next we have
 . This follows because
. This follows because  and both
and both  and
and  have the same altitudes, so their areas are proportional to their base lengths. Similarly, we have
have the same altitudes, so their areas are proportional to their base lengths. Similarly, we have  . At this stage, our simplified diagram is:
. At this stage, our simplified diagram is:

- Next we show that
 . Consider
. Consider  and
and  . Since
. Since  , these two triangles have the same areas, so
, these two triangles have the same areas, so  . That is,
. That is,  . Re-arranging this gives
. Re-arranging this gives  , or
, or  . Since both
. Since both  and
and  are positive (we’re dealing with internal division), we must have
are positive (we’re dealing with internal division), we must have  , so
, so  . Let’s adjust the diagram a bit:
. Let’s adjust the diagram a bit:

- Lastly we show that
 . Consider
. Consider  and
and  . They have the same altitudes, measured from their common vertex
. They have the same altitudes, measured from their common vertex  . Since
. Since  , their areas follow the same ratio, meaning that
, their areas follow the same ratio, meaning that  .
.

Thus we get
 as desired.
as desired.
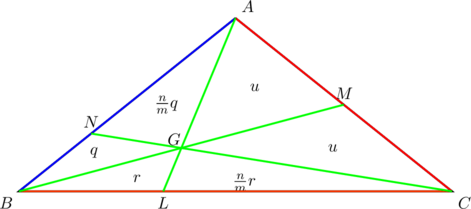
Suppose that ![]() ,
, ![]() , and
, and ![]() in the diagram below:
in the diagram below:

PROVE that at the point of concurrency, ![]() is divided in the ratio
is divided in the ratio ![]() ,
, ![]() is divided in the ratio
is divided in the ratio ![]() , and
, and ![]() is divided in the ratio
is divided in the ratio ![]() .
.
Let the point of concurrency be ![]() and let the area of
and let the area of ![]() be
be ![]() square units. Then, in terms of
square units. Then, in terms of ![]() , we have the following area diagram:
, we have the following area diagram:
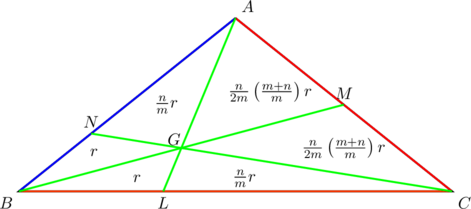
Consider ![]() and
and ![]() . They have the same altitudes, measured from their common vertex
. They have the same altitudes, measured from their common vertex ![]() . So the ratio of their areas gives the ratio of their base lengths. In other words,
. So the ratio of their areas gives the ratio of their base lengths. In other words, ![]() .
.
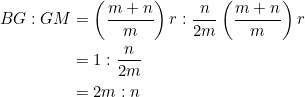
To show that ![]() , consider
, consider ![]() and
and ![]() . They have the same altitude, measured from their common vertex
. They have the same altitude, measured from their common vertex ![]() . So the ratio of their areas gives the ratio of their base lengths.
. So the ratio of their areas gives the ratio of their base lengths.
![Rendered by QuickLaTeX.com \begin{equation*} \begin{split} AG:GL&=\left[\frac{n}{2m}\left(\frac{m+n}{m}\right)r+\frac{n}{2m}\left(\frac{m+n}{m}\right)r\right]:\frac{n}{m}r\\ &=\frac{n}{m}\left(\frac{m+n}{m}\right)r:\frac{n}{m}r\\ &=\frac{m+n}{m}:1\\ &=(m+n):m \end{split} \end{equation*}](https://blog.fridaymath.com/wp-content/ql-cache/quicklatex.com-782fd74b2f302e69397aa68775ea4fb0_l3.png)
Similarly, ![]() .
.
PROVE that the centroid of a triangle divides the three medians in the ratio ![]() .
.
In the case of three medians, we have ![]() . So, using this in the previous example:
. So, using this in the previous example:
- the median
 is divided in the ratio
is divided in the ratio 
- the median
 is divided in the ratio
is divided in the ratio 
- the median
 is divided in the ratio
is divided in the ratio 
In ![]() ,
, ![]() is a median. In what ratio should cevians
is a median. In what ratio should cevians ![]() and
and ![]() divide sides
divide sides ![]() and
and ![]() so that the point of concurrency and the centroid trisect median
so that the point of concurrency and the centroid trisect median ![]() ?
?
Let ![]() be the centroid, and let the point of concurrency be
be the centroid, and let the point of concurrency be ![]() . Then
. Then ![]() divides median
divides median ![]() in ratio
in ratio ![]() , measured from vertex
, measured from vertex ![]() ; that is,
; that is, ![]() . Since
. Since ![]() is to be trisected, we want
is to be trisected, we want ![]() , or
, or ![]() . From the previous example, the median
. From the previous example, the median ![]() is divided in the ratio
is divided in the ratio ![]() at the point of concurrency. Therefore
at the point of concurrency. Therefore ![]() , or
, or ![]() . So cevian
. So cevian ![]() should divide side
should divide side ![]() in the ratio
in the ratio ![]() and cevian
and cevian ![]() should divide side
should divide side ![]() in the ratio
in the ratio ![]() .
.
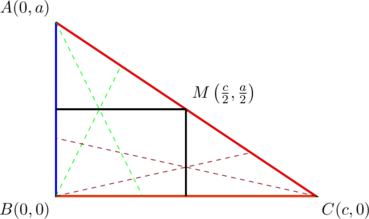
For any right triangle with legs parallel to the coordinate axes, PROVE that the slopes of its three medians form a geometric progression with common ratio ![]() .
.
For simplicity, fix the vertices at ![]() ,
, ![]() , and
, and ![]() ; a little modification will be needed for the general case.
; a little modification will be needed for the general case.
We now calculate the slopes of medians ![]() :
:

These form a geometric progression with common ratio of ![]() .
.
(There’s something interesting here. In our first post of this year, we saw that if the slopes of the sides of a triangle form a geometric sequence with ![]() as common ratio, then the triangle contains a vertical median and a horizontal median. Now, the above example says that if a triangle contains a vertical side and a horizontal side, then the slopes of its three medians form a geometric progression with a common ratio of
as common ratio, then the triangle contains a vertical median and a horizontal median. Now, the above example says that if a triangle contains a vertical side and a horizontal side, then the slopes of its three medians form a geometric progression with a common ratio of ![]() . Did you notice something? See exercise 5 at the end.)
. Did you notice something? See exercise 5 at the end.)
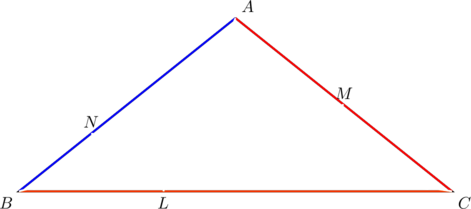
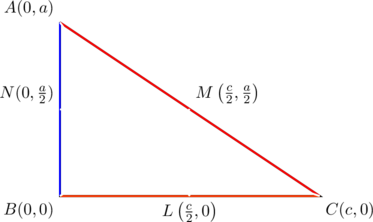
Give an example of a triangle in which one side, one median, and another cevian have slopes forming an arithmetic progression.
Consider ![]() below, in which
below, in which ![]() is a median,
is a median, ![]() is a cevian:
is a cevian:
The slopes of ![]() are
are ![]() , respectively. They form an arithmetic progression with a common difference of
, respectively. They form an arithmetic progression with a common difference of ![]() .
.
(Notice that if a third cevian is drawn from vertex ![]() and is concurrent with cevian
and is concurrent with cevian ![]() and median
and median ![]() , then it is an altitude. This is a good example of “mixing” and “matching” cevians as used in our post’s title. Mixing means that they are different; matching means that they are concurrent.)
, then it is an altitude. This is a good example of “mixing” and “matching” cevians as used in our post’s title. Mixing means that they are different; matching means that they are concurrent.)
Takeaway
The ratios we considered in this post (![]() ) were for convenience. There are other ratios that can still ensure concurrency.
) were for convenience. There are other ratios that can still ensure concurrency.
Tasks
- Let
 be the vertices of
be the vertices of  . If there are cevians
. If there are cevians  which divide sides
which divide sides  in the ratios
in the ratios  , respectively:
, respectively:
- PROVE that the point of concurrency has coordinates
 ;
; - Deduce that the centroid of
 is the point
is the point  .
.
- PROVE that the point of concurrency has coordinates
 has vertices at
has vertices at  . Assuming cevians
. Assuming cevians  divide sides
divide sides  in the ratios
in the ratios  , respectively, and they concur at the point
, respectively, and they concur at the point  , determine
, determine  and
and  .
. has vertices at
has vertices at  . Determine the lengths of cevians
. Determine the lengths of cevians  which divide sides
which divide sides  in the ratios
in the ratios  , respectively.
, respectively.- Let
 be a right triangle in the first quadrant, with vertices
be a right triangle in the first quadrant, with vertices  ,
,  , and
, and  . For
. For  , PROVE that there are three cevians
, PROVE that there are three cevians  whose slopes form a geometric progression with common ratio
whose slopes form a geometric progression with common ratio  .
.
(Compare this with Example 9.) - Let
 be the vertices of
be the vertices of  . Let the slopes of medians through
. Let the slopes of medians through  be denoted by
be denoted by  , respectively. Suppose that
, respectively. Suppose that  (in that order) form a geometric progression with a common ratio of
(in that order) form a geometric progression with a common ratio of  . PROVE that:
. PROVE that:
 ;
; .
.
(In view of Example 9, conclude that the slopes of the three medians of a triangle form a geometric progression with common ratio if, and only if, the triangle is a right triangle with legs parallel to the coordinate axes.)
if, and only if, the triangle is a right triangle with legs parallel to the coordinate axes.)
- (Opposite slopes) The right triangle
 with vertices at
with vertices at  ,
,  ,
,  has very nice properties:
has very nice properties:

- Find an internal point
 on
on  such that the slope of cevian
such that the slope of cevian  is the negative of the slope of cevian
is the negative of the slope of cevian  , and PROVE that these two cevians intersect at
, and PROVE that these two cevians intersect at  ;
; - Find an internal point
 on
on  such that the slope of cevian
such that the slope of cevian  is the negative of the slope of cevian
is the negative of the slope of cevian  , and PROVE that these two cevians intersect at
, and PROVE that these two cevians intersect at  ;
; - If a cevian from
 and a cevian from
and a cevian from  have opposite slopes, is their point of intersection always of the form
have opposite slopes, is their point of intersection always of the form  for some
for some  ?
? - For any point
 between
between  and
and  , PROVE that there is a point
, PROVE that there is a point  between
between  and
and  such that the slopes of cevians
such that the slopes of cevians  and
and  are negatives of each other;
are negatives of each other; - For any point
 between
between  and
and  , PROVE that there is a point
, PROVE that there is a point  between
between  and
and  such that the slopes of cevians
such that the slopes of cevians  and
and  are negatives of each other.
are negatives of each other.
- Find an internal point
- Consider the right triangle
 with vertices at
with vertices at  ,
,  ,
,  :
:

An arbitrary point
 on
on  can be given by the coordinates
can be given by the coordinates  , where
, where  . PROVE that:
. PROVE that: if and only if
if and only if  ;
; if and only if
if and only if  ;
;- for
 and
and  , cevians
, cevians  and
and  have opposite slopes;
have opposite slopes; - for
 and
and  , cevians
, cevians  and
and  have opposite slopes;
have opposite slopes; - a cevian from
 and a cevian from
and a cevian from  intersect at
intersect at  if and only if they have opposite slopes (and
if and only if they have opposite slopes (and  );
); - a cevian from
 and a cevian from
and a cevian from  intersect at
intersect at  if and only if they have opposite slopes (and
if and only if they have opposite slopes (and  ).
).
- Let
 be the vertices of
be the vertices of  . Suppose that the slopes of sides
. Suppose that the slopes of sides  and
and  are negatives of each other, and that the slopes of medians through
are negatives of each other, and that the slopes of medians through  and
and  are also negatives of each other. PROVE that:
are also negatives of each other. PROVE that:
-
 (so
(so  form an arithmetic sequence)
form an arithmetic sequence)  (so
(so  is isosceles)
is isosceles)- the median through vertex
 is vertical.
is vertical.
-
- PROVE that if the slopes of the equal sides of an isosceles triangle are negatives of each other, then the
 -coordinates form an arithmetic progression.
-coordinates form an arithmetic progression. - For an integer
 , let
, let  be the vertices of
be the vertices of  . PROVE that a cevian from vertex
. PROVE that a cevian from vertex  divides side
divides side  in the ratio
in the ratio  if and only if it is an altitude.
if and only if it is an altitude.