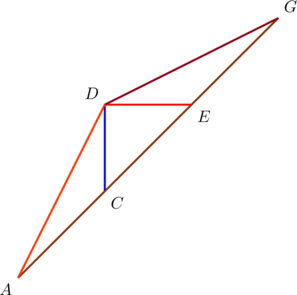
In case you’ve used a staircase before, you’ve “experienced” a special case of a geometric sequence as a consequence.
For a case study, consider the diagram below:
Join ![]() to
to ![]() ,
, ![]() to
to ![]() , and
, and ![]() to
to ![]() to form
to form ![]() :
:
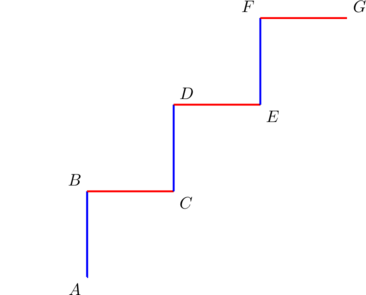
We’ll prove that the slopes of the sides of ![]() form a geometric sequence, if
form a geometric sequence, if ![]() .
.
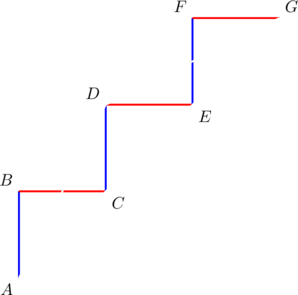
Example
A portion of a staircase is shown below:
Verify that the slopes of the sides of ![]() form a geometric sequence.
form a geometric sequence.
Easy-peasy.
The slopes of sides ![]() are
are ![]() , respectively. They form a geometric sequence with a common ratio
, respectively. They form a geometric sequence with a common ratio ![]() .
.
(The fact that the slope of side ![]() is
is ![]() implies that it makes an angle of
implies that it makes an angle of ![]() with the horizontal. In real life, however, the angle is usually around
with the horizontal. In real life, however, the angle is usually around ![]() .)
.)
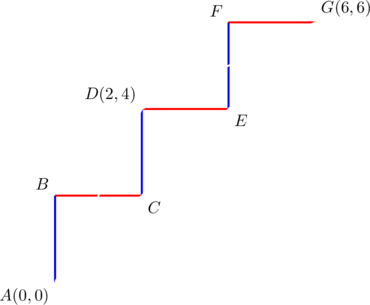
Example
A portion of a staircase is shown below:
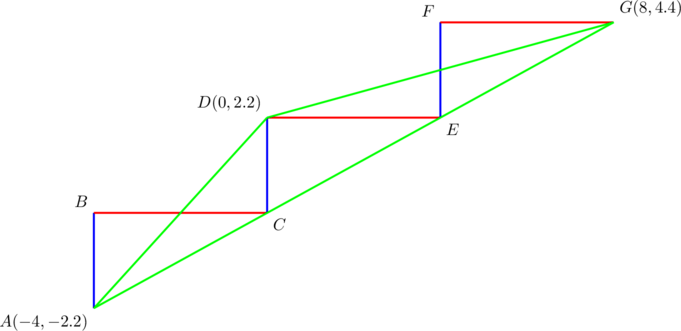
Verify that the slopes of the sides of ![]() form a geometric sequence.
form a geometric sequence.
Easy-peasy as before.
The slopes of sides ![]() are
are ![]() , respectively. They form a geometric sequence with a common ratio of
, respectively. They form a geometric sequence with a common ratio of ![]() .
.
(It shouldn’t come as a surprise that the common ratio is ![]() this time too. Indeed, it is almost always the case in a staircase, because the “rise” and “run” stay constant throughout the entire span of the staircase. For this reason, the geometric sequence obtained on a staircase is a special case.)
this time too. Indeed, it is almost always the case in a staircase, because the “rise” and “run” stay constant throughout the entire span of the staircase. For this reason, the geometric sequence obtained on a staircase is a special case.)
Basic background
From Example 3 to Example 6 below, we lay the foundation for our staircase story. Don’t worry if it seems to “escalate” quite quickly; remember we’re on a staircase ![]() .
.
PROVE that if the slopes of the sides of a triangle form a geometric sequence with a positive common ratio, then the triangle contains an obtuse angle.
Actually, any triangle in which the three sides have positive slopes contains an obtuse angle (for now we’re content with slopes in geometric sequence).
Let ![]() be such that sides
be such that sides ![]() have slopes
have slopes ![]() , respectively. If the common ratio
, respectively. If the common ratio ![]() is positive, then the angle at
is positive, then the angle at ![]() is obtuse. To see this, let the lengths of sides
is obtuse. To see this, let the lengths of sides ![]() be
be ![]() , respectively. Then, as we’ll show in our next post, the following pseudo-pythagorean property holds:
, respectively. Then, as we’ll show in our next post, the following pseudo-pythagorean property holds:
![]()
Thus, we can use the cosine law to compute the cosine of the angle at ![]() :
:
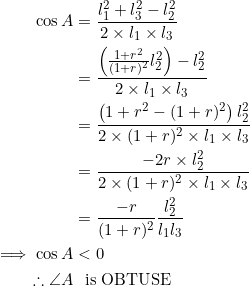
The obtuse angle at ![]() is well-oriented in such a way that a special
is well-oriented in such a way that a special ![]() can be cut out from it.
can be cut out from it.
In ![]() , let
, let ![]() be the slopes of sides
be the slopes of sides ![]() , respectively. Then a point
, respectively. Then a point ![]() divides
divides ![]() in the ratio
in the ratio ![]() if and only if it shares the same
if and only if it shares the same ![]() -coordinate as vertex
-coordinate as vertex ![]() .
.
Thus, ![]() will be a vertical line. Take note of this.
will be a vertical line. Take note of this.
The problem deals with coordinates, so let’s begin by specifying the coordinates of the vertices of the parent triangle ![]() . Assume
. Assume ![]() are the vertices. Since the slopes of sides
are the vertices. Since the slopes of sides ![]() are
are ![]() , there are relationships among the coordinates:
, there are relationships among the coordinates:
(1) 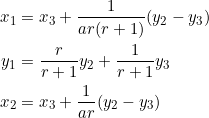
Now, suppose a point ![]() divides side
divides side ![]() in the ratio
in the ratio ![]() , with
, with ![]() . Using the formula for internal division of a line segment, we can write the
. Using the formula for internal division of a line segment, we can write the ![]() -coordinate of point
-coordinate of point ![]() in terms of the
in terms of the ![]() -coordinates of
-coordinates of ![]() and
and ![]() as follows:
as follows:
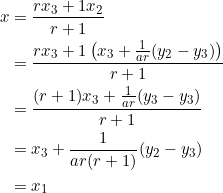
Therefore, point ![]() shares the same
shares the same ![]() -coordinate as vertex
-coordinate as vertex ![]() .
.
Conversely, suppose that point ![]() shares the same
shares the same ![]() -coordinate as vertex
-coordinate as vertex ![]() . We proceed to find the
. We proceed to find the ![]() -coordinate of
-coordinate of ![]() . Since the slope of
. Since the slope of ![]() is
is ![]() and it goes through
and it goes through ![]() , its equation is
, its equation is ![]() . Using the fact that
. Using the fact that ![]() at point
at point ![]() , we have:
, we have:
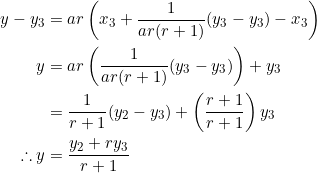
Let’s manipulate ![]() slightly:
slightly:
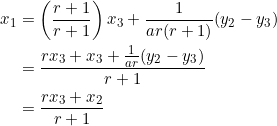
Thus, ![]() is the point
is the point ![]() . By examining its coordinates, we see that it actually divides side
. By examining its coordinates, we see that it actually divides side ![]() in the ratio
in the ratio ![]() .
.
In ![]() , let
, let ![]() be the slopes of sides
be the slopes of sides ![]() , respectively. Then a point
, respectively. Then a point ![]() divides
divides ![]() in the ratio
in the ratio ![]() if and only if it shares the same
if and only if it shares the same ![]() -coordinate as vertex
-coordinate as vertex ![]() .
.
Thus, ![]() will be a horizontal line. Together with the previous example, the parent
will be a horizontal line. Together with the previous example, the parent ![]() contains a special right triangle
contains a special right triangle ![]() in which both legs
in which both legs ![]() and
and ![]() are parallel to the coordinate axes. Further,
are parallel to the coordinate axes. Further, ![]() . The presence of this right triangle is key to our staircase story.
. The presence of this right triangle is key to our staircase story.
Let’s find the ![]() coordinate of point
coordinate of point ![]() which divides
which divides ![]() in the ratio
in the ratio ![]() . Using equation (1) and the formula for internal division of a line segment:
. Using equation (1) and the formula for internal division of a line segment:
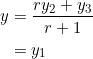
Easier than thought. Conversely, suppose that ![]() shares the same
shares the same ![]() -coordinate as vertex
-coordinate as vertex ![]() , so that
, so that ![]() . We’ll find its
. We’ll find its ![]() -coordinate, using the fact that it lies on side
-coordinate, using the fact that it lies on side ![]() whose equation is
whose equation is ![]() :
:
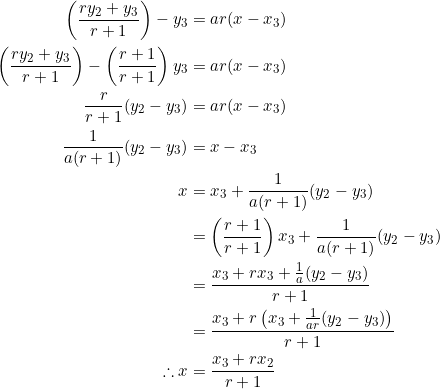
These calculations show that ![]() is the point
is the point ![]() , and it divides side
, and it divides side ![]() in the ratio
in the ratio ![]() if we inspect its coordinates.
if we inspect its coordinates.
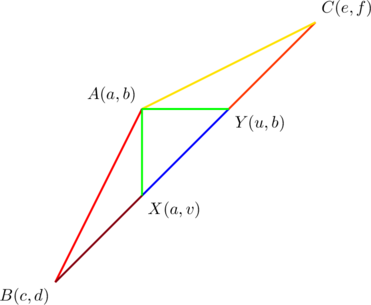
In the above diagram, point ![]() divides
divides ![]() in the ratio
in the ratio ![]() while point
while point ![]() divides
divides ![]() in the ratio
in the ratio ![]() .
.
(Main goal)
Let ![]() be a triangle. Then the following two statements are equivalent:
be a triangle. Then the following two statements are equivalent:
- the slopes of the sides form a geometric sequence with positive common ratio;
- there are internal points
 and
and  on
on  such that
such that  is vertical,
is vertical,  is horizontal, and
is horizontal, and  .
.
The implication ![]() follows from the three previous examples. For
follows from the three previous examples. For ![]() , consider the diagram below:
, consider the diagram below:
(2) ![]()
Since ![]() , we have:
, we have:
![]()
Because ![]() are co-linear, we have
are co-linear, we have ![]() , and so
, and so ![]() . Using this in the previous equation, we have:
. Using this in the previous equation, we have:
![Rendered by QuickLaTeX.com \begin{equation*} \begin{split} (a-c)^2+(v-d)^2&=\left[(e-u)\left(\frac{v-d}{a-c}\right)\right]^2+(e-u)^2\\ (a-c)^2+(v-d)^2&=(e-u)^2\left[\frac{(v-d)^2+(a-c)^2}{(a-c)^2}\right]\\ \therefore (a-c)^2&=(e-u)^2 \end{split} \end{equation*}](https://blog.fridaymath.com/wp-content/ql-cache/quicklatex.com-9d118a4597d95d6a517f8713561f7ae7_l3.png)
The latter means that either ![]() or
or ![]() . However, in our diagram we have
. However, in our diagram we have ![]() and
and ![]() , thus ruling out the possibility of
, thus ruling out the possibility of ![]() . We therefore settle for
. We therefore settle for ![]() .
.
Returning to (2) and using some equality relations among the slopes of the co-linear points ![]() , we have:
, we have:
![Rendered by QuickLaTeX.com \begin{equation*} \begin{split} \left(\frac{f-d}{e-c}\right)^2&=\left(\frac{b-v}{u-a}\right)^2\\ \left(\frac{f-b}{e-a}\right)\left(\frac{b-d}{a-c}\right)&=\left[(e-u)\frac{b-v}{u-a}\right].\frac{1}{e-a}\left(\frac{b-d}{a-c}\right)\\ &=\left(\frac{b-v}{u-a}\right)\left(\frac{b-d}{e-a}\right)\\ &=\left(\frac{b-v}{u-a}\right)\left(\frac{b-d}{u-c}\right)\\ &=\left(\frac{b-v}{u-a}\right)\left(\frac{b-v}{u-a}\right) \end{split} \end{equation*}](https://blog.fridaymath.com/wp-content/ql-cache/quicklatex.com-3a905b562287039a1b71d82b26339bf8_l3.png)
This proves that the slopes of the sides of ![]() form a geometric progression. The common ratio is positive in view of the diagram.
form a geometric progression. The common ratio is positive in view of the diagram.
In ![]() , let
, let ![]() be the slopes of sides
be the slopes of sides ![]() , respectively. For any positive integer
, respectively. For any positive integer ![]() , PROVE that there are points
, PROVE that there are points ![]() and
and ![]() on
on ![]() such that the slopes of the sides of
such that the slopes of the sides of ![]() form a geometric sequence
form a geometric sequence ![]() .
.
Note that both Example 4 and Example 5 result from the special case ![]() , but the associated slopes do not form a geometric sequence. Also,
, but the associated slopes do not form a geometric sequence. Also, ![]() need not be a positive integer; any positive number works as well.
need not be a positive integer; any positive number works as well.
We need to construct points ![]() and
and ![]() first.
first.
Let ![]() be the point which divides side
be the point which divides side ![]() in the ratio
in the ratio ![]() . (The restriction that
. (The restriction that ![]() is essential to exclude the midpoint of
is essential to exclude the midpoint of ![]() .) Using equation (1) and the formula for internal division of a line segment, we can determine the coordinates of
.) Using equation (1) and the formula for internal division of a line segment, we can determine the coordinates of ![]() as follows:
as follows:
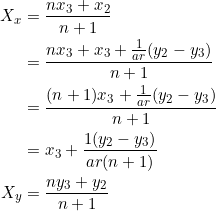
So, ![]() is the point
is the point ![]() . Next, let’s construct point
. Next, let’s construct point ![]() by dividing side
by dividing side ![]() in the ratio
in the ratio ![]() .
.
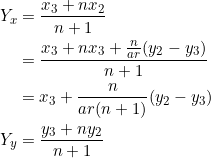
Thus, ![]() is the point
is the point ![]() . Together with equation (1), the vertices of
. Together with equation (1), the vertices of ![]() are:
are:
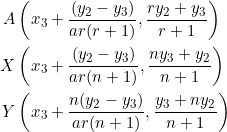
From these, we obtain ![]() as the slopes of sides
as the slopes of sides ![]() , respectively. Note that
, respectively. Note that ![]() yields
yields ![]() as the slopes of
as the slopes of ![]() — same slopes as those of the parent triangle
— same slopes as those of the parent triangle ![]() .
.
The next example shows that if we exclude three points from ![]() , namely, the midpoint of
, namely, the midpoint of ![]() , the point on
, the point on ![]() that shares the same
that shares the same ![]() -coordinate as
-coordinate as ![]() , and the point on
, and the point on ![]() that shares the same
that shares the same ![]() -coordinate as
-coordinate as ![]() , then we obtain what may be regarded as a stronger version of Example 6.
, then we obtain what may be regarded as a stronger version of Example 6.
For any ![]() , the following statements are equivalent:
, the following statements are equivalent:
- the slopes of sides
 form a geometric sequence with positive common ratio;
form a geometric sequence with positive common ratio; - for any internal point
 on
on  , there is an internal point
, there is an internal point  on
on  such that
such that  and the slopes of
and the slopes of  form a geometric sequence.
form a geometric sequence.
Bear in mind the three excluded points on ![]() . Basically, these are the points where the slope of
. Basically, these are the points where the slope of ![]() will be undefined, the slope of
will be undefined, the slope of ![]() will be zero, and where
will be zero, and where ![]() . Naturally, these were excluded to ensure that we have proper slopes.
. Naturally, these were excluded to ensure that we have proper slopes.
To show ![]() , let
, let ![]() be the point which divides
be the point which divides ![]() in the ratio
in the ratio ![]() , where
, where ![]() is a positive integer. Choose
is a positive integer. Choose ![]() as the point which divides
as the point which divides ![]() in the ratio
in the ratio ![]() . Then
. Then ![]() . By Example 7, the slopes of the sides of
. By Example 7, the slopes of the sides of ![]() form a geometric progression.
form a geometric progression.
To show ![]() , take
, take ![]() . Then
. Then ![]() has to be taken as
has to be taken as ![]() , so that the equality
, so that the equality ![]() is satisfied (both sides being zero).
is satisfied (both sides being zero).
PROVE that the two infinite geometric progressions
(3) ![]()
(4) ![]()
can be obtained from the same triangle.
You already know how to generate (4); if not, see here. So we focus on obtaining (3), following a similar procedure and using the same triangle that yields (4).
Begin with a triangle whose slopes are ![]() — like the one shown below:
— like the one shown below:
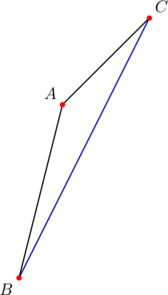
where ![]() ,
, ![]() ,
, ![]() are the vertices.
are the vertices.
For an integer ![]() , set
, set ![]() . Then
. Then ![]() is an internal point on
is an internal point on ![]() ; further,
; further, ![]() as
as ![]() and
and ![]() as
as ![]() . These limits ensure that
. These limits ensure that ![]() always resides within side
always resides within side ![]() .
.
Next, let’s compute the slope of cevian ![]() for each
for each ![]() :
:
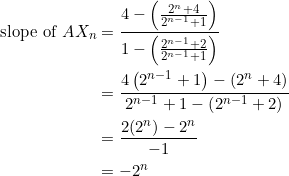
Letting ![]() gives rise to the infinite geometric sequence in (3).
gives rise to the infinite geometric sequence in (3).
That special right triangle
We conclude by isolating a unique property of the special right triangle that appears in staircases.
PROVE that a triangle is a right triangle with legs parallel to the coordinate axes if and only if the slopes of its three medians form a geometric sequence with common ratio ![]() .
.
First suppose that we have a right triangle with legs parallel to the coordinate axes. This direction of the proof was done in our previous post, but let’s go through it briefly. Fix the vertices at ![]() ,
, ![]() , and
, and ![]() ; a little modification will be needed for the general case.
; a little modification will be needed for the general case.
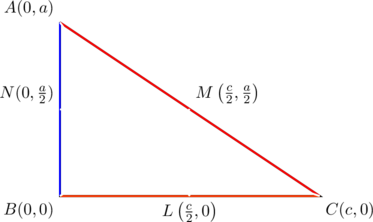
Now calculate the slopes of medians ![]() :
:

These form a geometric progression with common ratio of ![]() .
.
Conversely, suppose that we have ![]() with vertices
with vertices ![]() ,
, ![]() , and
, and ![]() in such a way that the slopes of the three medians form a geometric sequence with common ratio
in such a way that the slopes of the three medians form a geometric sequence with common ratio ![]() .
.
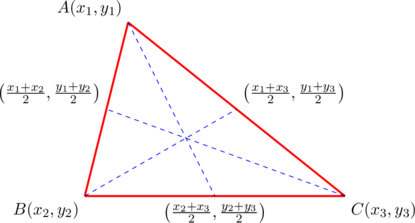
If we denote the slopes of the medians from vertices ![]() by
by ![]() respectively, then:
respectively, then:
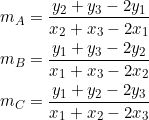
Suppose that the geometric sequence of median slopes is ![]() , then
, then ![]() , and
, and ![]() :
:
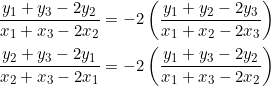
Clear fractions from the first equation above:
(5) ![]()
Now clear fractions from the second equation:
(6) ![]()
It turns out that ![]() can be eliminated if we perform the operation
can be eliminated if we perform the operation ![]() (5)-(6):
(5)-(6):
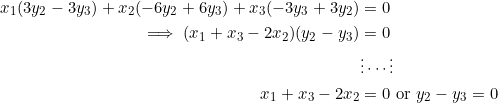
Since the slopes of the three medians form a geometric sequence, we can’t have ![]() . Otherwise this would result in an undefined slope for the median from vertex
. Otherwise this would result in an undefined slope for the median from vertex ![]() , namely
, namely ![]() , and a geometric sequence cannot contain such a term. So the only option is to take
, and a geometric sequence cannot contain such a term. So the only option is to take ![]() , whence
, whence ![]() . Our triangle now has one side parallel to the
. Our triangle now has one side parallel to the ![]() -axis.
-axis.
Put ![]() in equation (5):
in equation (5):
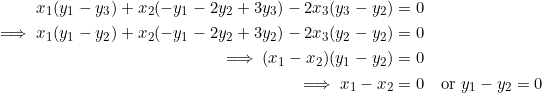
Since we already had ![]() , it’s impossible to have
, it’s impossible to have ![]() in addition, otherwise this would lead to
in addition, otherwise this would lead to ![]() , which is not allowed for a triangle. So we take
, which is not allowed for a triangle. So we take ![]() , whence
, whence ![]() . Our triangle now has a side that is parallel to the
. Our triangle now has a side that is parallel to the ![]() -axis.
-axis.
Therefore, ![]() has side
has side ![]() parallel to the
parallel to the ![]() -axis, and side
-axis, and side ![]() parallel to the
parallel to the ![]() -axis.
-axis.
Takeaway
We’ve used staircases in various cases and in various places — homes, airports, train stations, offices, etc. As we ascend our staircase, we “run” forward and “rise” higher, so our slopes are positive. In turn, the geometric sequence we describe has a positive common ratio — in most cases, ![]() .
.
Embellished with nice properties, triangles with slopes in geometric progression are established as objects to cherish and relish. And, they not only appeal in theory, they appear in real life too.
Tasks
- (Three out) Given
 with vertices
with vertices  , the slopes of the sides form a geometric sequence with common ratio
, the slopes of the sides form a geometric sequence with common ratio  . Find two points
. Find two points  and
and  on
on  for which the slopes of the sides of
for which the slopes of the sides of  do not form a geometric sequence.
do not form a geometric sequence.
(The third point is the midpoint of , namely
, namely  . Apart from these three points, given any other point
. Apart from these three points, given any other point  within
within  , there is a corresponding point
, there is a corresponding point  within
within  for which the slopes of the sides of
for which the slopes of the sides of  form a geometric sequence.)
form a geometric sequence.) - Consider the diagram below:

in which
 and
and  have the same
have the same  -coordinates,
-coordinates,  and
and  share the same
share the same  -coordinates, and
-coordinates, and  .
.- If also
 , PROVE that the slopes of the sides of
, PROVE that the slopes of the sides of  form a geometric sequence with a common ratio of
form a geometric sequence with a common ratio of  ;
; - Give an example to show that if
 and
and  do not trisect
do not trisect  , then the common ratio is no longer
, then the common ratio is no longer  .
.
- If also
- PROVE that if the slopes of the sides of a triangle are all positive (and non-zero), then the triangle contains an obtuse angle.
(Similarly, if the slopes are all negative, there’ll be an obtuse angle.) - In
 , let
, let  be the slopes of sides
be the slopes of sides  , respectively. If
, respectively. If  , PROVE that side
, PROVE that side  is the longest side.
is the longest side. - In
 , let
, let  be the slopes of sides
be the slopes of sides  , respectively. If
, respectively. If  , PROVE that side
, PROVE that side  is NOT always the longest side.
is NOT always the longest side. - PROVE that the two infinite geometric sequences
 and
and  can be obtained from the same triangle, using slopes.
can be obtained from the same triangle, using slopes. - (Close enough) Let
 be a triangle in which sides
be a triangle in which sides  have slopes
have slopes  , with
, with  and
and  . Let
. Let  and
and  be points on
be points on  which divide
which divide  in the ratios
in the ratios  and
and  . PROVE that the area of
. PROVE that the area of  is
is  times the area of
times the area of  .
.
(In the limit , we have area of
, we have area of 
 area of
area of  .)
.) - Find coordinates for the vertices
 of a non-right triangle
of a non-right triangle  which contains a right triangle
which contains a right triangle  such that the area of
such that the area of  is
is  times the area of
times the area of  .
. - Let
 be such that the slopes of sides
be such that the slopes of sides  form the geometric sequence
form the geometric sequence  , with
, with  .
.
- Let
 be the point which divides
be the point which divides  in the ratio
in the ratio  and let
and let  be the midpoint of
be the midpoint of  and
and  . PROVE that the slope of cevian
. PROVE that the slope of cevian  is
is  times the slope of
times the slope of  .
. - Let
 be the point which divides
be the point which divides  in the ratio
in the ratio  and let
and let  be the midpoint of
be the midpoint of  and
and  . PROVE that the slope of cevian
. PROVE that the slope of cevian  is
is  times the slope of
times the slope of  .
. - Conclude that every triangle with slopes
 (where
(where  ) contains a sub-triangle with slopes
) contains a sub-triangle with slopes  , a geometric sequence with common ratio
, a geometric sequence with common ratio  .
.
- Let
- (Right inside) Let
 (
( ) be the slopes of sides
) be the slopes of sides  in
in  . PROVE that there are points
. PROVE that there are points  and
and  on
on  for which
for which  .
. - Let
 (
( ) be the slopes of sides
) be the slopes of sides  in
in  . PROVE that there two points
. PROVE that there two points  and
and  on
on  for which the slopes of
for which the slopes of  form an arithmetic sequence with a common difference of
form an arithmetic sequence with a common difference of  , namely:
, namely:  .
. - Let
 (
( ) be the slopes of sides
) be the slopes of sides  in
in  . PROVE that there two points
. PROVE that there two points  and
and  on
on  for which the slopes of
for which the slopes of  form an arithmetic sequence with a common difference of
form an arithmetic sequence with a common difference of  , namely:
, namely:  .
. - Let
 ,
,  ,
,  be a right triangle in the first quadrant. Choose any vertex, say
be a right triangle in the first quadrant. Choose any vertex, say  , and draw two cevians
, and draw two cevians  and
and  to side
to side  .
.
- For a positive integer
 , let
, let  and
and  divide side
divide side  in the ratios
in the ratios  and
and  , respectively. PROVE that
, respectively. PROVE that  and
and  have the same centroid
have the same centroid - Can this be extended to all triangles?
- For a positive integer
- (Almost right) Let
 be the slopes of sides
be the slopes of sides  in
in  . PROVE that there are points
. PROVE that there are points  and
and  on
on  such that
such that 
(Compare this with exercise 10 above.)
Today is a special day in this poster’s life. As such, he gives praise to the Owner of life. Mind always goes back to that marked Thursday, June 14, 2018. In turn, it C–A–N–`–T hold back from giving thanks. What happened was very basic (as simple as HTML), but its effect became “drastic” (actually, dramatic, dynamic), and so one’s gratitude is made public. Hopefully this poster’s gratitude to the Heavenly Father doesn’t ruffle your feathers. If it does, please (don’t bother to) read further. May you find that “spark” you need to start what will lead you to succeed.
Thanksgiving
To the reader:
Wish: