We’re s--o excited about this!!! As in, E–X–C–I–T–E–D!!! Indeed, this is expected, considering what is to be expounded: “any” geometric sequence ![]() can be encapsulated as slopes of a simple triangle like the one below:
can be encapsulated as slopes of a simple triangle like the one below:
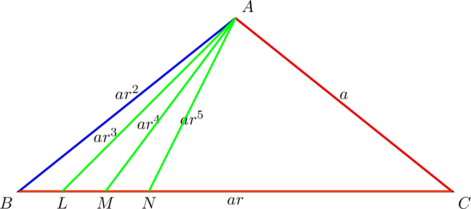
And the procedure is easy: first find a triangle with slopes ![]() , then the remaining terms
, then the remaining terms ![]() can be obtained as slopes of line segments drawn from a fixed vertex
can be obtained as slopes of line segments drawn from a fixed vertex ![]() to a fixed side
to a fixed side ![]() .
.
Positive common ratio
![]()
that is, (positive) powers of ![]() .
.
Example
Find coordinates for the vertices of ![]() with slopes
with slopes ![]() .
.
There are different ways to obtain a triangle whose slopes are ![]() . One can begin with an arbitrary point
. One can begin with an arbitrary point ![]() . Then the two other points can be chosen as
. Then the two other points can be chosen as ![]() and
and ![]() . With these, the slopes of sides
. With these, the slopes of sides ![]() will be
will be ![]() , respectively.
, respectively.
In the present case, let’s first choose ![]() as
as ![]() , for simplicity. Since the sequence is
, for simplicity. Since the sequence is ![]() , we have
, we have ![]() and
and ![]() . So
. So ![]() and
and ![]() .
.
The entire geometric sequence ![]() can be obtained from the above triangle.
can be obtained from the above triangle.
Example
For each ![]() , PROVE that
, PROVE that ![]() lies within
lies within ![]() , where
, where ![]() is the point
is the point ![]() and
and ![]() is the point
is the point ![]() .
.
Note that ![]() is a point on
is a point on ![]() . Let’s use distances to show that it’s indeed internal. We prove that
. Let’s use distances to show that it’s indeed internal. We prove that ![]() .
.
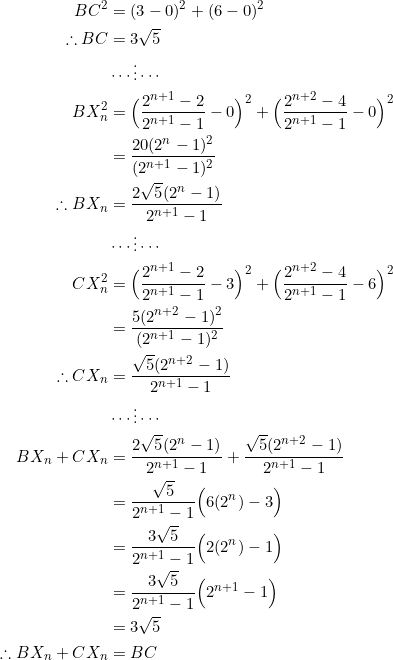
This proves that for each ![]() , the point
, the point ![]() lies internally on
lies internally on ![]() .
.
Example
For each ![]() , let
, let ![]() . PROVE that the slope of
. PROVE that the slope of ![]() is
is ![]() , where
, where ![]() is the point
is the point ![]() .
.
This follows by direct calculation:
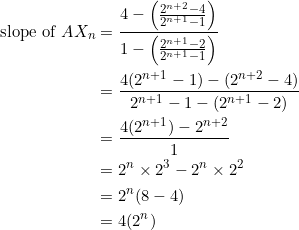
Thus, when ![]() , the corresponding slopes will be
, the corresponding slopes will be ![]() ; that is,
; that is, ![]() .
.
By defining ![]() and using
and using ![]() with vertices at
with vertices at ![]() , we’ve seen that the entire geometric progression
, we’ve seen that the entire geometric progression ![]() can be obtained as slopes of the line segments
can be obtained as slopes of the line segments ![]() , together with
, together with ![]() with slope
with slope ![]() . Notice that when
. Notice that when ![]() ,
, ![]() becomes
becomes ![]() and when
and when ![]() ,
, ![]() becomes
becomes ![]() . What happens to
. What happens to ![]() when
when ![]() ?
?
![Rendered by QuickLaTeX.com \[\boxed{\frac{4-\frac{4}{3}}{1-\frac{2}{3}}=\frac{\frac{8}{3}}{\frac{1}{3}}=8=4(2^1)}\]](https://blog.fridaymath.com/wp-content/ql-cache/quicklatex.com-3152a53c74fef6ac043f6c575c7f4f64_l3.png)
as expected.
Put ![]() , then
, then ![]() has coordinates
has coordinates ![]() . Together with
. Together with ![]() , the slope of line segment
, the slope of line segment ![]() is
is
![Rendered by QuickLaTeX.com \[\boxed{\frac{4-\frac{12}{7}}{1-\frac{6}{7}}=\frac{\frac{16}{7}}{\frac{1}{7}}=16=4(2^2)}\]](https://blog.fridaymath.com/wp-content/ql-cache/quicklatex.com-b3b6dac5a6947ee8bc3adcdcee48b7dc_l3.png)
as expected.
Put ![]() , then
, then ![]() has coordinates
has coordinates ![]() . Together with
. Together with ![]() , the slope of line segment
, the slope of line segment ![]() is
is
![Rendered by QuickLaTeX.com \[\boxed{\frac{4-\frac{28}{15}}{1-\frac{14}{15}}=\frac{\frac{32}{15}}{\frac{1}{15}}=32=4(2^3)}\]](https://blog.fridaymath.com/wp-content/ql-cache/quicklatex.com-3f43ca6ba30984c4cfc487b8fc195ed0_l3.png)
as expected.
Three things to note from the above calculation:
- the points
 are defined relative to the chosen coordinates for
are defined relative to the chosen coordinates for  ;
; - the line segments
 that describe the geometric progression do not get to the midpoint of side
that describe the geometric progression do not get to the midpoint of side  ;
; - the roles of vertex
 and side
and side  cannot be altered; doing so will distort the orderly arrangement of the line segments. See the next two examples.
cannot be altered; doing so will distort the orderly arrangement of the line segments. See the next two examples.
Example
Given ![]() with vertices
with vertices ![]() , find coordinates for a point
, find coordinates for a point ![]() on
on ![]() such that the slope of the line segment
such that the slope of the line segment ![]() is
is ![]() .
.
Let’s find the equations of ![]() and
and ![]() and then solve the resulting linear system:
and then solve the resulting linear system:
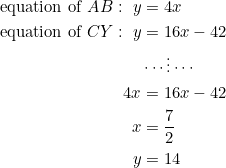
Thus, ![]() is the point
is the point ![]() . It is external to side
. It is external to side ![]() — we don’t want that.
— we don’t want that.
Example
Given ![]() with vertices
with vertices ![]() , find coordinates for a point
, find coordinates for a point ![]() on
on ![]() such that the slope of the line segment
such that the slope of the line segment ![]() is
is ![]() .
.
Let’s find the equations of ![]() and
and ![]() and then solve the resulting linear system:
and then solve the resulting linear system:
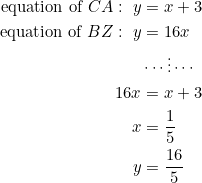
Thus, ![]() is the point
is the point ![]() . It is external to side
. It is external to side ![]() — we don’t want that.
— we don’t want that.
![]()
Example
Find coordinates for the vertices of ![]() whose side slopes are
whose side slopes are ![]() .
.
Take ![]() . Then the slope of
. Then the slope of ![]() is
is ![]() , the slope of
, the slope of ![]() is
is ![]() , and the slope of
, and the slope of ![]() is
is ![]() .
.
Example
Let ![]() . For each
. For each ![]() , PROVE that the slope of the line segment
, PROVE that the slope of the line segment ![]() is
is ![]() , where
, where ![]() is the point
is the point ![]() .
.
Observe that each ![]() lies within
lies within ![]() (
(![]() ). By direct calculation:
). By direct calculation:
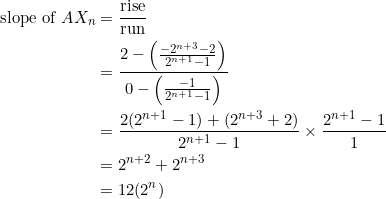
Thus, we obtain the geometric progression ![]() by putting
by putting ![]() . Together with the first three terms that are the slopes of the original triangle, we obtain the entire geometric progression
. Together with the first three terms that are the slopes of the original triangle, we obtain the entire geometric progression ![]() .
.
![]()
Example
Explain how to obtain the entire geometric progression ![]() as slopes.
as slopes.
Easy-peasy.
Begin with a ![]() in which the slopes of the sides are
in which the slopes of the sides are ![]() . To this end, take
. To this end, take ![]() . Then the slope of
. Then the slope of ![]() is
is ![]() , the slope of
, the slope of ![]() is
is ![]() , and the slope of
, and the slope of ![]() is
is ![]() .
.
Next, let ![]() . Then, by direct calculation (as in and ), the slope of
. Then, by direct calculation (as in and ), the slope of ![]() is
is ![]() , for
, for ![]() . Therefore, letting
. Therefore, letting ![]() successively, we obtain the terms
successively, we obtain the terms ![]() . If we now append the slopes of the sides of
. If we now append the slopes of the sides of ![]() (which are
(which are ![]() ), we obtain the entire geometric progression
), we obtain the entire geometric progression ![]() .
.
Reciprocal terms
In addition to obtaining ![]() , we also get
, we also get ![]() , once we go past a certain point; let’s call it a terminal point (see the exercises at the end
, once we go past a certain point; let’s call it a terminal point (see the exercises at the end ![]() ).
).
Example
Given ![]() with vertices
with vertices ![]() , find coordinates for a point
, find coordinates for a point ![]() on
on ![]() such that the slope of
such that the slope of ![]() is
is ![]() .
.
In Example we had ![]() . Put
. Put ![]() , then
, then ![]() . Take
. Take ![]() . Then
. Then ![]() is an internal point on
is an internal point on ![]() ; further, the slope of
; further, the slope of ![]() is
is
![]()
as desired. Similarly, by putting ![]() , we obtain the terms
, we obtain the terms ![]() . Thus, inside a simple, single triangle lies the infinite geometric progression
. Thus, inside a simple, single triangle lies the infinite geometric progression
![]()
disguised as slopes.
Example
Given ![]() with vertices
with vertices ![]() , let
, let ![]() . PROVE that
. PROVE that ![]() .
.
Put ![]() , then
, then ![]() . Put
. Put ![]() , then
, then ![]() , as also found in a previous example. By the distance formula:
, as also found in a previous example. By the distance formula:
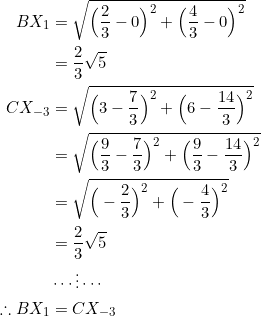
Observe that the slopes of the sides of ![]() are
are ![]() ; they form a geometric progression with a common ratio of
; they form a geometric progression with a common ratio of ![]() , which is the square of the common ratio of the geometric progression
, which is the square of the common ratio of the geometric progression ![]() formed by the slopes of the sides of the parent
formed by the slopes of the sides of the parent ![]() .
.
Takeaway
Slopes are usually introduced sometime in grade ![]() (or earlier), while geometric sequences are usually studied in grade
(or earlier), while geometric sequences are usually studied in grade ![]() (or earlier). Here, we’ve managed to show a close connection between the two concepts, using the medium of a triangle.
(or earlier). Here, we’ve managed to show a close connection between the two concepts, using the medium of a triangle.
Throughout we worked with positive integer common ratios. But the common ratios can also be negative, and in such cases things become much more exciting.
Tasks
- (Depressed cubic) Consider
 with vertices
with vertices  . PROVE that:
. PROVE that:
- the foot of the altitude from vertex
 is
is  ;
; - the length of the altitude from vertex
 is
is  ;
; - the area of
 is
is  (this becomes a depressed cubic if written in the form
(this becomes a depressed cubic if written in the form  . Moreover, if
. Moreover, if  is an integer (
is an integer ( of course), then this area is always a positive integer).
of course), then this area is always a positive integer).
- the foot of the altitude from vertex
- Let
 . PROVE that
. PROVE that  as
as  .
. - Let
 . PROVE that
. PROVE that  as
as  .
. - (Special points) Given
 with vertices
with vertices  , PROVE that there are (internal) points
, PROVE that there are (internal) points  and
and  on
on  such that:
such that:
- the slope of
 is undefined and the slope of
is undefined and the slope of  is zero (
is zero ( for vertical,
for vertical,  for horizontal);
for horizontal);  and
and  trisect side
trisect side  (
( );
);- the areas of
 are
are  sq. unit each (making the overall area of
sq. unit each (making the overall area of  to be
to be  sq. units).
sq. units).
- the slope of
- (Higher powers) Given
 with vertices at
with vertices at  , the slopes of its sides form a geometric progression with common ratio
, the slopes of its sides form a geometric progression with common ratio  . Find two points
. Find two points  and
and  on
on  such that the slopes of the sides of
such that the slopes of the sides of  form a geometric progression with common ratio
form a geometric progression with common ratio  .
. - (Negative region) Given
 with vertices
with vertices  , find two points
, find two points  and
and  on
on  such that the slope of any line segment
such that the slope of any line segment  , where
, where  is a point between
is a point between  and
and  , is negative.
, is negative. - (Base five) Explain how to generate the geometric progression
 using slopes.
using slopes. - (Base six) Explain how to generate the geometric progression
 using slopes.
using slopes. - (Base seven) Explain how to generate the geometric progression
 using slopes.
using slopes. - (Terminal point) Given
 with vertices
with vertices  , determine the coordinates of the terminal point
, determine the coordinates of the terminal point  on
on  (a point on
(a point on  such that the slope of the line segment
such that the slope of the line segment  is
is  ; this is also where the slopes of the line segments from vertex
; this is also where the slopes of the line segments from vertex  change from positive powers of
change from positive powers of  to negative powers of
to negative powers of  ).
).