The depressed cubic as area – High School Geometry

We investigated the area property of our very own triangle, and guess what! The depressed cubic showed up.

Ww!!! How???

Consider $\triangle ABC$ with vertices at $A(1,r^2),B(0,0),C(1+r,r+r^2)$ , where $0,\pm 1\neq r$ . PROVE that its area $\Delta$ can be given by $\Delta=\frac{r^3-r}{2}$ .

Easy-peasy.

We were given the coordinates $A(1,r^2),B(0,0),C(1+r,r+r^2)$ . We simply use the well-known area formula

$\Delta=\frac{y_1(x_3-x_2)+y_2(x_1-x_3)+y_3(x_2-x_1)}{2}$

and, by taking $(x_1,y_1)=(1,r^2)$ , $(x_2,y_2)=(0,0)$ , $(x_3,y_3)=(1+r,r+r^2)$ , we obtain

$\begin{equation*} \begin{split} \Delta&=\frac{r^2(1+r-0)+0(1-(1+r))+(r+r^2)(0-1)}{2}\\ &=\frac{r^2(1+r)+(r+r^2)(-1)}{2}\\ &=\frac{r^2(r+1)-r(r+1)}{2}\\ &=\frac{(r+1)(r^2-r)}{2}\\ &=\frac{(r-1).r.(r+1)}{2}\\ \textrm{Or,}~\Delta&=\frac{r^3-r}{2} \end{split} \end{equation*}$

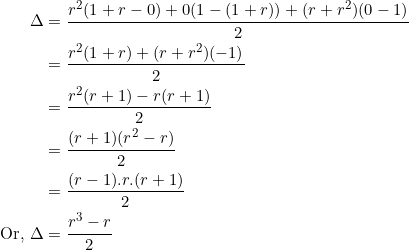
Observe that the numerator contains three consecutive factors, namely $r-1,r$ , and $r+1$ . Thus, if $r$ is an integer, then at least one of the three will be even, and so the resulting product $(r-1).r.(r+1)$ will be even. This means that the area $\Big(=\frac{(r-1).r.(r+1)}{2}\Big)$ will be an integer — and a multiple of a triangular number.

The depressed cubic

A cubic equation of the form $\boxed{x^3+Ax=B}$ in which the second degree term $x^2$ is missing, is usually called a depressed cubic. For a discussion on how to solve such equations, see here.

Suppose we re-arrange our area formula $\Delta=\frac{r^3-r}{2}$ as

$r^3-r = 2\Delta,$

then we obtain not just a depressed cubic, but a restricted, simplified, specialized, depressed cubic. As such, its solution also takes a relatively simplified form.

PROVE that the area formula obtained previously, namely $\Delta=\frac{r(r^2-1)}{2}$ , is an odd function.

Recall that an odd function $f(x)$ satisfies $f(-x)=-f(x)$ . Let’s write $\Delta(r)=\frac{r(r^2-1)}{2}$ . Then

$\begin{equation*} \begin{split} \Delta(-r)&=\frac{(-r)\Big((-r)^2-1\Big)}{2}\\ &=\frac{(-r)\Big(r^2-1\Big)}{2}\\ &=-\frac{r\Big(r^2-1\Big)}{2}\\ &=-\Delta(r) \end{split} \end{equation*}$

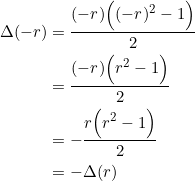
One implication of this “oddness” is that two opposite values of $r$ will yield the “same” area. As such, when we solve the depressed cubic equation

$r^3-r=2\Delta$

for $r$ , we must remember that any solution we obtain has a corresponding opposite, but the associated opposite doesn’t arise as a solution of the depressed cubic. For example, if $r=2$ is a solution of the depressed cubic, then we must also consider $r=-2$ , despite the fact that $r=-2$ is not a solution of the depressed cubic (see the exercises at the end).

For the depressed cubic $r^3-r=2\Delta$ , PROVE that $r$ can be given in terms of $\Delta$ by: $\boxed{r=\sqrt[3]{\frac{9\Delta+\sqrt{81\Delta^2-3}}{9}}-\sqrt[3]{\frac{-9\Delta+\sqrt{81\Delta^2-3}}{9}}}$

Let’s do this!

Following the standard method of solving a depressed cubic, we seek $s$ and $t$ such that $3st=-1$ and $s^3-t^3=2\Delta$ . Then, $r=s-t$ is a solution of $r^3-r=2\Delta$ . Indeed, we have:

$\begin{equation*} \begin{split} r^3-r&=(s-t)^3-(s-t)\\ &=(s^3-3s^2t+3st^2-t^3)-(s-t)\\ &=(s^3-t^3)-3st(s-t)-(s-t)\\ &=2\Delta-(-1)(s-t)-(s-t)\quad\textrm{by assumption}\\ &=2\Delta+(s-t)-(s-t)\\ &=2\Delta \end{split} \end{equation*}$

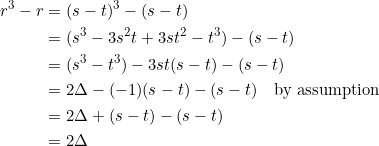
So it remains to find such $s$ and $t$ that satisfy $s^3-t^3=2\Delta$ and $3st=-1$ . Isolate $t$ from the second equation: $t=-\frac{1}{3s}$ . Substituting, the equation $s^3-t^3=2\Delta$ becomes:

$s^3-\Big(-\frac{1}{3s}\Big)^3=2\Delta \implies s^3+\frac{1}{27s^3}=2\Delta$

Clear fractions and bring all terms to the left side:

$27s^6-(54\Delta)s^3+1=0 \implies 27(s^3)^2-(54\Delta)s^3+1=0$

Since this is now a quadratic in $s^3$ , we can use the quadratic formula to isolate $s^3$ . Doing this gives:

$s^3=\frac{54\Delta\pm\sqrt{(54\Delta)^2-4\times 27\times 1}}{2\times 27}$

Simplifying,

$s^3=\frac{9\Delta\pm\sqrt{81\Delta^2-3}}{9},~\textrm{or}~s=\sqrt[3]{\frac{9\Delta\pm\sqrt{81\Delta^2-3}}{9}}.$

It suffices to take $s=\sqrt[3]{\frac{9\Delta+\sqrt{81\Delta^2-3}}{9}}$ . Then, $s^3-t^3=2\Delta$ gives $t^3=s^3-2\Delta$ :

$\begin{equation*} \begin{split} t^3&=\frac{9\Delta+\sqrt{81\Delta^2-3}}{9}-2\Delta\\ &=\frac{9\Delta+\sqrt{81\Delta^2-3}}{9}-\frac{18\Delta}{9}\\ &=\frac{-9\Delta+\sqrt{81\Delta^2-3}}{9}\\ \implies t&=\sqrt[3]{\frac{-9\Delta+\sqrt{81\Delta^2-3}}{9}} \end{split} \end{equation*}$

Finally,

$r=s-t=\sqrt[3]{\frac{9\Delta+\sqrt{81\Delta^2-3}}{9}}-\sqrt[3]{\frac{-9\Delta+\sqrt{81\Delta^2-3}}{9}}.$

Using the preceding example, PROVE that $\Delta=\frac{\sqrt{3}}{9}$ if, and only if, $r=\frac{2\sqrt{3}}{3}$ .

First suppose that $\Delta=\frac{\sqrt{3}}{9}$ . Then $81\Delta^2-3=0$ . And so

$r=\sqrt[3]{\frac{9\Delta+\sqrt{81\Delta^2-3}}{9}}-\sqrt[3]{\frac{-9\Delta+\sqrt{81\Delta^2-3}}{9}}$

reduces to

$\begin{equation*} \begin{split} r&=\sqrt[3]{\Delta}-\sqrt[3]{-\Delta}\\ &=2\sqrt[3]{\Delta}\\ &=2\sqrt[3]{\frac{\sqrt{3}}{9}}\\ &=\frac{2\sqrt{3}}{3} \end{split} \end{equation*}$

Conversely, if $r=\frac{2\sqrt{3}}{3}$ , then from the depressed cubic equation $r^3-r=2\Delta$ , we obtain

$\begin{equation*} \begin{split} \Delta&=\frac{r^3-r^}{2}\\ &=\frac{r(r^2-1)}{2}\\ &=\frac{\frac{2\sqrt{3}}{3}\Big[\Big(\frac{2\sqrt{3}}{3}\Big)^2-1\Big]}{2}\\ &=\frac{2\sqrt{3}}{3}\times\frac{1}{3}\times\frac{1}{2}\\ &=\frac{\sqrt{3}}{9} \end{split} \end{equation*}$

Discuss the nature of the roots of the depressed cubic $r^3-r=2\Delta$ .

We use the cubic discriminant to this end. For a general cubic $ax^3+bx^2+cx+d$ , its discriminant is given by the quantity

$\boxed{b^2c^2-4ac^3-4b^3d-27a^2d^2+18abcd}$

Putting $a=1$ , $b=0$ , $c=-1$ , and $d=-2\Delta$ , we obtain, for the depressed cubic $r^3-r=2\Delta$ :

$0^2(-1)^2-4(1)(-1)^3-4(0^3)(-2\Delta)-27(1^2)(-2\Delta)^2+18(1)(0)(-1)(-2\Delta),$

which reduces to $4-108\Delta^2$ . Consequently:

if $4-108\Delta^2=0$ , then the depressed cubic has three real roots, one of which is repeated;
if $4-108\Delta^2> 0$ , then the depressed cubic has three distinct real roots;
if $4-108\Delta^2< 0$ , the depressed cubic has one real root and two complex roots.

Solve the depressed cubic equation $r^3-r=2\frac{\sqrt{3}}{9}$ .

Observe that this is the case in which $\Delta=\frac{\sqrt{3}}{9}$ . The corresponding cubic discriminant $4-108\Delta^2$ becomes $4-108\times\frac{1}{27}=0$ . As such, we expect a repeated root. From Example 4, one of the roots is $r=\frac{2\sqrt{3}}{3}$ . Accordingly, $\Big(r-\frac{2\sqrt{3}}{3}\Big)$ is a factor of $r^3-r-2\frac{\sqrt{3}}{9}$ . By long division, we get the quadratic factor $\Big(r^2+\frac{2\sqrt{3}}{3}r+\frac{1}{3}\Big)$ , which is a perfect square:

$\Big(r^2+\frac{2\sqrt{3}}{3}r+\frac{1}{3}\Big)=\Big(r+\frac{\sqrt{3}}{3}\Big)^2.$

Thus, the complete solution to $r^3-r=2\frac{\sqrt{3}}{9}$ is $r=-\frac{\sqrt{3}}{3},~\frac{2\sqrt{3}}{3}$ . Notice how this solution set becomes “increased” in the next example.

Example

$\triangle ABC$ has an area of $\Delta=\frac{\sqrt{3}}{9}$ . The slopes of its sides form a geometric sequence $1,r,r^2$ . Find possible coordinates for the vertices $A,B,C$ .

Since the slopes of the sides form the geometric sequence $1,r,r^2$ , we can place the vertices at $A(1,r^2)$ , $B(0,0)$ , and $C(1+r,r+r^2)$ . The area will then be $\frac{r^3-r}{2}$ , in view of Example 1. But we’re given that the area is $\Delta=\frac{\sqrt{3}}{9}$ :

$\frac{r^3-r}{2}=\frac{\sqrt{3}}{9}\implies r^3-r=2\frac{\sqrt{3}}{9},$

which is the depressed cubic solved in the preceding example. Recall that the cubic has $r=\frac{-\sqrt{3}}{3},~\frac{2\sqrt{3}}{3}$ as solutions.

Being that the area formula $\Delta=\frac{r^3-r}{2}$ is an odd function (Example 2), we should also consider $r=\frac{\sqrt{3}}{3},~-\frac{2\sqrt{3}}{3}$ as possible values for the common ratio $r$ , even though these are not solutions to the depressed cubic.

for $r=\frac{-\sqrt{3}}{3}$ , the coordinates will be $A\left(1,\frac{1}{3}\right)$ , $B(0,0)$ , $C\left(1-\frac{\sqrt{3}}{3},~-\frac{\sqrt{3}}{3}+\frac{1}{3}\right)=\left(\frac{3-\sqrt{3}}{3},\frac{1-\sqrt{3}}{3}\right)$ ;
for $r=\frac{\sqrt{3}}{3}$ , the coordinates will be $A\left(1,\frac{1}{3}\right)$ , $B(0,0)$ , $C\left(1+\frac{\sqrt{3}}{3},~\frac{\sqrt{3}}{3}+\frac{1}{3}\right)=\left(\frac{3+\sqrt{3}}{3},\frac{1+\sqrt{3}}{3}\right)$ ;
for $r=\frac{-2\sqrt{3}}{3}$ , the coordinates will be $A\left(1,\frac{4}{3}\right)$ , $B(0,0)$ , $C\left(1-\frac{2\sqrt{3}}{3},~-\frac{2\sqrt{3}}{3}+\frac{4}{3}\right)=\left(\frac{3-2\sqrt{3}}{3},\frac{4-2\sqrt{3}}{3}\right)$ ;
for $r=\frac{2\sqrt{3}}{3}$ , the coordinates will be $A\left(1,\frac{4}{3}\right)$ , $B(0,0)$ , $C\left(1+\frac{2\sqrt{3}}{3},~\frac{2\sqrt{3}}{3}+\frac{4}{3}\right)=\left(\frac{3+2\sqrt{3}}{3},\frac{4+2\sqrt{3}}{3}\right)$ .

Since the area $\Delta=\frac{\sqrt{3}}{9}$ is so small, each case produces a rare-listic diagram when drawn.

Example (“Fixed point”)

Find coordinates for the vertices of a $\triangle ABC$ whose slopes are $1,r,r^2$ and whose area is $\sqrt{3}$ sq. units.

We solve the cubic equation $r^3-r=2\Delta$ using $\Delta=\sqrt{3}$ :

$r^3-r=2\sqrt{3}\implies (r-\sqrt{3})(r^2+\sqrt{3}r+2)=0\implies r=\sqrt{3};$

the quadratic part has complex roots. Again, we should consider $r=-\sqrt{3}$ , despite the fact that it’s not a solution to the current cubic equation.

Next, let’s use the coordinates $A(1,r^2)$ , $B(0,0)$ , $C(1+r,r+r^2)$ :

$A(1,3),B(0,0),C(1+\sqrt{3},3+\sqrt{3}),\quad\textrm{OR}\quad A(1,3),B(0,0),C(1-\sqrt{3},3-\sqrt{3}).$

In this case, the area and the common ratio are the same.

Give an example of a scalene triangle with non-zero side slopes, irrational side lengths, and an integer area.

The only challenge with this question is the non-zero slopes requirement; otherwise we could just have taken a triangle with one side on the $x$ -axis and the rest becomes easy.

Luckily, we can always turn to triangles with slopes in geometric progressions. In this case we take $\triangle ABC$ with vertices at $A(1,4),B(0,0),C(3,6)$ . The side slopes are $1,2,4$ . For the side lengths we have $AB=\sqrt{17}$ , $BC=3\sqrt{5}$ , and $CA=2\sqrt{2}$ , all irrational and all different, so the triangle is scalene. Its area is $3$ sq. units.

Let $\alpha$ be a root of the depressed cubic $r^3-r-2\Delta=0$ . PROVE that $r^3-r-2\Delta=(r-\alpha)(r^2+\alpha r+\frac{2\Delta}{\alpha})$ .

Since $\Delta\neq 0$ (an area), it follows that $\alpha\neq 0$ as well. This ensures that the quantity $\frac{2\Delta}{\alpha}$ is defined.

Set

$r^3-r-2\Delta=(r-\alpha)(r^2+br+c)=r^3+(b-\alpha)r^2+(c-\alpha b)r-\alpha c.$

Comparing coefficients of like terms, $b-\alpha=0,~c-\alpha b=-1$ , and $\alpha c=2\Delta$ . So $b=\alpha$ , $c=\alpha b-1=\alpha^2-1$ , and again $c=\frac{2\Delta}{\alpha}$ . The two expressions for $c$ yield $\alpha(\alpha^2-1)=2\Delta$ , which is valid because $\alpha$ is a root of the original cubic $r^3-r-2\Delta=0$ .

$\therefore r^3-r-2\Delta=(r-\alpha)(r^2+\alpha r+\frac{2\Delta}{\alpha}).$

Takeaway

If $\triangle ABC$ with vertices at $A(x_1,y_1),B(x_2,y_2),C(x_3,y_3)$ is such that the slopes of sides $AB,BC,CA$ are $a,ar,ar^2$ , respectively, then the area $\Delta$ of the triangle can be given by

$\Delta=\frac{1}{2}\Big(\frac{r-1}{r+1}\Big)\Big(\frac{1}{ar}\Big)(y_2-y_3)^2.$

By restricting the coordinates in a suitable way (see the exercises below), we obtain the depressed cubic $\frac{1}{2}r(r^2-1)$ as the area.

Tasks

(Special square) For any right triangle with vertices $(\alpha_1,\beta_1)$ , $(\alpha_2,\beta_2)$ , and $(\alpha_3,\beta_3)$ , PROVE that: $\Big(\frac{|\alpha_2-\alpha_1|+|\beta_2-\beta_1|}{|\alpha_3-\alpha_3|+|\beta_3-\beta_1|}\Big)^2=\frac{(\alpha_2-\alpha_1)^2+(\beta_2-\beta_1)^2}{(\alpha_3-\alpha_1)^2+(\beta_3-\beta_1)^2}.$
(Notice how squaring respects addition in this case. In addition, not all four absolute values on the left are absolutely necessary $\cdots\vdots\cdots$ .)
(Special square) For any triangle with centroid $(\alpha_1,\beta_1)$ , circumcenter $(\alpha_2,\beta_2)$ , and orthocenter $(\alpha_3,\beta_3)$ , PROVE that: $\Big(\frac{(\alpha_2-\alpha_1)+(\beta_2-\beta_1)}{(\alpha_3-\alpha_3)+(\beta_3-\beta_1)}\Big)^2=\frac{(\alpha_2-\alpha_1)^2+(\beta_2-\beta_1)^2}{(\alpha_3-\alpha_1)^2+(\beta_3-\beta_1)^2}.$
(Notice the absolute absence of absolute values in this case — so long as $(\alpha_2-\alpha_1)+(\beta_2-\beta_1)\neq 0$ and $(\alpha_3-\alpha_1)+(\beta_3-\beta_1)\neq 0$ . Also, any right triangle satisfies this property “TWICE” — with its regular vertices, and also with its three principal centers.)
(Opposite roots) PROVE that if a depressed cubic $x^3+Ax=B$ has two opposite solutions, namely $x=\alpha$ and $x=-\alpha$ , then $B=0$ .
(In our own case, the right member $B$ represents the area $\Delta$ of a certain, obscure triangle. Since $\Delta\neq 0$ , this explains why the depressed cubic equation $r^3-r=2\Delta$ cannot have two opposite solutions.)
has vertices at . Assume that the slopes of sides are , in that order.
- PROVE that its area $\Delta$ can be given by $\Delta=\frac{1}{2}\Big(\frac{r-1}{r+1}\Big)\Big(\frac{1}{ar}\Big)(y_2-y_3)^2.$
- Find an appropriate choice of $(y_2-y_3)$ for which the area $\Delta$ reduces to the depressed cubic $\Delta=\frac{a}{2}r(r^2-1).$
has vertices at , , . PROVE that:
- the coordinates of the foot of the altitude from vertex $A$ is $\Big(x_1+\frac{a^2r^3+1}{a^2r^2+1},~y_1+\frac{a^3r^4+ar}{a^2r^2+1}\Big)$ ;
- the length of the altitude from vertex $A$ is $h=\frac{ar(r-1)}{a^2r^2+1}$ ;
- the area of $\triangle ABC$ is $\frac{a}{2}(r-1)(r)(r+1)=\frac{a}{2}r(r^2-1)$ .
Consider with vertices at , , . Its side slopes are , a geometric progression in which and .
- Use the area formula in exercise 4 above to compute its area;
- Use the area formula in exercise 5 above to compute its area;
- Compute its area in the regular way, using $\frac{y_1(x_3-x_2)+y_2(x_1-x_3)+y_3(x_2-x_1)}{2}$ ;
- Explain why the formula in exercise 5 did not work correctly in this case.
For with vertices at , , , PROVE that:
- its centroid is located at $\Big(\frac{2+r}{3},\frac{r+2r^2}{3}\Big)$ ;
- its circumcenter is at $\Big(\frac{r^3+r^2+r-1}{2(r-1)},\frac{r^3-r^2-r-1}{2(r-1)}\Big)$ ;
- its orthocenter is at $\Big(\frac{1+r^3}{1-r},\frac{-1-r^3}{1-r}\Big)$ ;
- the slope of its Euler line is $m_{E}=-\Big(\frac{r^3+r^2+r+3}{3r^3+r^2+r+1}\Big)$ .
(Same ratio) Given $A(1,r^2)$ , $B(0,0)$ , $C(1+r,r+r^2)$ , PROVE that the centroid, the circumcenter, and the orthocenter of $\triangle ABC$ lie on parallel lines $x+y=\frac{2}{3}(1+r+r^2)$ , $x+y=1+r+r^2$ , and $x+y=0$ , respectively.
(Notice that the line through the centroid is in the middle of the other two lines. Moreover, these lines preserve the usual $1:2$ ratio in which the centroid divides the circumcenter-orthocenter distance.)
If $\sqrt[3]{a+\sqrt{b}}=c+\sqrt{d}$ , PROVE that $\sqrt[3]{-a+\sqrt{b}}=-c+\sqrt{d}$ .
(Unit area) Find coordinates for the vertices of $\triangle ABC$ with slopes $1,r,r^2$ and an area of $1$ sq. unit.