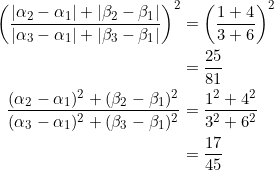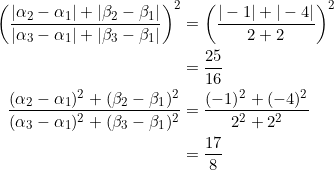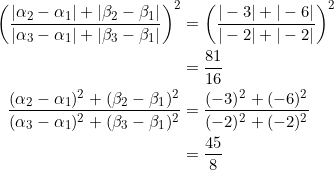The process of squaring (and taking square root) can sometimes preserve the operation of addition, as in this equation:
(1) ![]()
We show that if we take ![]() as the centroid,
as the centroid, ![]() as the circumcenter, and
as the circumcenter, and ![]() as the orthocenter of any triangle, then the equation always holds — evaluating to
as the orthocenter of any triangle, then the equation always holds — evaluating to ![]() in every case.
in every case.
Interestingly, if we append absolute values, then the equation holds twice for a right triangle — with ![]() as the vertex containing angle
as the vertex containing angle ![]() , while
, while ![]() and
and ![]() are the other two vertices:
are the other two vertices:
(2) ![]()
The latter equation is preferred to the former one, and is behind a little geometric application that we present.
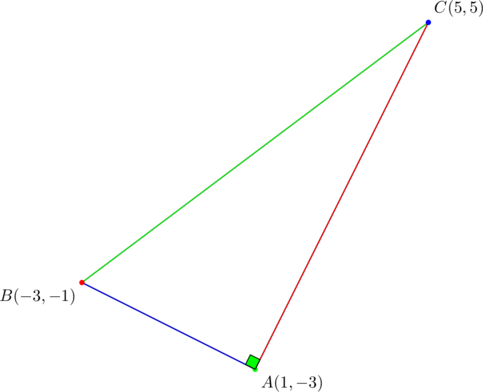
Consider ![]() with vertices at
with vertices at ![]() ,
, ![]() , and
, and ![]() . VERIFY that equation (2) holds in this case.
. VERIFY that equation (2) holds in this case.
Using ![]() ,
, ![]() , and
, and ![]() , we have, from equation (2) that:
, we have, from equation (2) that:
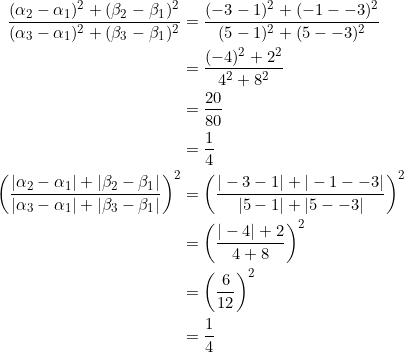
CL!!!!!!!!!!!
Consider the same ![]() in the previous example:
in the previous example: ![]() ,
, ![]() ,
, ![]() . Using
. Using ![]() as the centroid,
as the centroid, ![]() as the circumcenter, and
as the circumcenter, and ![]() as the orthocenter, VERIFY that equation (1) holds.
as the orthocenter, VERIFY that equation (1) holds.
Since ![]() is a right triangle, its circumcenter is the midpoint of the hypotenuse (in this case the midpoint of side
is a right triangle, its circumcenter is the midpoint of the hypotenuse (in this case the midpoint of side ![]() ), and its orthocenter is at the vertex containing angle
), and its orthocenter is at the vertex containing angle ![]() (vertex
(vertex ![]() ). The centroid is obtained as in any other triangle, using
). The centroid is obtained as in any other triangle, using ![]() or
or ![]() in the present case.
in the present case.
So we have ![]() ,
, ![]() , and
, and ![]() . In equation (1):
. In equation (1):
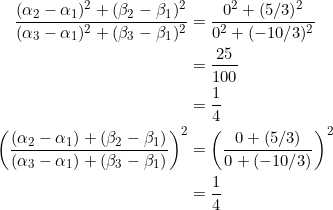
CL!!!
Right company:
In our next example we show that equation (2) doesn’t hold for a triangle that’s not right.
Consider a triangle with vertices ![]() ,
, ![]() ,
, ![]() . PROVE that equation (2) fails in this case.
. PROVE that equation (2) fails in this case.
We will select ![]() as any of the three vertices. This leads to three possibilities:
as any of the three vertices. This leads to three possibilities:
- Case I: let
 ,
,  , and
, and  .
.

- Case II: let
 ,
,  , and
, and  .
.

- Case III: let
 ,
,  , and
, and  .
.

Although equation (2) fails for this triangle, equation (1) still holds, so long as we take ![]() as the centroid,
as the centroid, ![]() as the circumcenter, and
as the circumcenter, and ![]() as the orthocenter.
as the orthocenter.
Co-linear points
PROVE that equation (1) holds if the points ![]() ,
, ![]() , and
, and ![]() lie on the same straight line (co-linear).
lie on the same straight line (co-linear).
Ignoring degeneracies (like ![]() etc), we’re to prove that
etc), we’re to prove that
![]()
based on the co-linearity of the given points. [In the case where the slope of the line is ![]() , absolute values will be necessary on the left. As a result of this, it is generally preferable to use equation (2).]
, absolute values will be necessary on the left. As a result of this, it is generally preferable to use equation (2).]
Co-linearity ensures that the slope between any two points will be the same, so we have:
![]()
Then
![Rendered by QuickLaTeX.com \begin{equation*} \begin{split} \left(\frac{(\alpha_2-\alpha_1)+(\beta_2-\beta_1)}{(\alpha_3-\alpha_1)+(\beta_3-\beta_1)}\right)^2&=\left(\frac{(\alpha_2-\alpha_1)+\left(\frac{\beta_3-\beta_1}{\alpha_3-\alpha_1}\right)(\alpha_2-\alpha_1)}{(\alpha_3-\alpha_1)+(\beta_3-\beta_1)}\right)^2\\ &=\left(\frac{\alpha_2-\alpha_1}{\alpha_3-\alpha_1}\right)^2\\ \frac{(\alpha_2-\alpha_1)^2+(\beta_2-\beta_1)^2}{(\alpha_3-\alpha_1)^2+(\beta_3-\beta_1)^2}&=\frac{(\alpha_2-\alpha_1)^2+\left[\left(\frac{\beta_3-\beta_1}{\alpha_3-\alpha_1}\right)(\alpha_2-\alpha_1)\right]^2}{(\alpha_3-\alpha_1)^2+(\beta_3-\beta_1)^2}\\ &=\frac{(\alpha_2-\alpha_1)^2}{(\alpha_3-\alpha_1)^2} \end{split} \end{equation*}](https://blog.fridaymath.com/wp-content/ql-cache/quicklatex.com-1c64a5caa8ff9fc0e7854ced5993015c_l3.png)
In any triangle, let ![]() ,
, ![]() , and
, and ![]() be the centroid, circumcenter, and orthocenter, respectively. PROVE that equation (1) is satisfied, and that both sides evaluate to
be the centroid, circumcenter, and orthocenter, respectively. PROVE that equation (1) is satisfied, and that both sides evaluate to ![]() .
.
This follows from the preceding example together with the well-known fact that these three principal triangle centers are co-linear.
To show that both sides evaluate to ![]() , consider the right member of equation (1):
, consider the right member of equation (1):
![]()
where the numerator represents the square of the circumcenter-centroid distance, and the denominator represents the square of the centroid-orthocenter distance. Since the centroid divides the circumcenter-orthocenter distance in the ratio ![]() , the right side always reduces to
, the right side always reduces to ![]() And so is the left side.
And so is the left side.
Square root:
Equation (1) can be re-written as (if one wants, one can place absolute values on each term on the right):
![Rendered by QuickLaTeX.com \[\sqrt{\frac{(\alpha_2-\alpha_1)^2+(\beta_2-\beta_1)^2}{(\alpha_3-\alpha_1)^2+(\beta_3-\beta_1)^2}}=\frac{(\alpha_2-\alpha_1)+(\beta_2-\beta_1)}{(\alpha_3-\alpha_1)+(\beta_3-\beta_1)}\]](https://blog.fridaymath.com/wp-content/ql-cache/quicklatex.com-0448332683651fc9808418f77ab3b252_l3.png)
and so even square roots preserve addition in this situation.
Opposite slopes
In any triangle in which two sides have opposite slopes, PROVE that equation (2) is satisfied.
Let ![]() be the vertex from which the sides with opposite slopes originate, and let
be the vertex from which the sides with opposite slopes originate, and let ![]() and
and ![]() be the two other vertices. We show that:
be the two other vertices. We show that:
![]()
By assumption
![]()
The remainder of the proof is akin to that of the previous example; the only difference is the inclusion of absolute values:
![Rendered by QuickLaTeX.com \begin{equation*} \begin{split} \left(\frac{|\alpha_2-\alpha_1|+|\beta_2-\beta_1|}{|\alpha_3-\alpha_1|+|\beta_3-\beta_1|}\right)^2&=\left(\frac{|\alpha_2-\alpha_1|+\left |-\left(\frac{\beta_3-\beta_1}{\alpha_3-\alpha_1}\right)(\alpha_2-\alpha_1)\right |}{|\alpha_3-\alpha_1|+|\beta_3-\beta_1|}\right)^2\\ &=\left(\frac{\alpha_2-\alpha_1}{\alpha_3-\alpha_1}\right)^2\\ \frac{(\alpha_2-\alpha_1)^2+(\beta_2-\beta_1)^2}{(\alpha_3-\alpha_1)^2+(\beta_3-\beta_1)^2}&=\frac{(\alpha_2-\alpha_1)^2+\left[-\left(\frac{\beta_3-\beta_1}{\alpha_3-\alpha_1}\right)(\alpha_2-\alpha_1)\right]^2}{(\alpha_3-\alpha_1)^2+(\beta_3-\beta_1)^2}\\ &=\frac{(\alpha_2-\alpha_1)^2}{(\alpha_3-\alpha_1)^2} \end{split} \end{equation*}](https://blog.fridaymath.com/wp-content/ql-cache/quicklatex.com-4e0adf36967393d34499ce6c4e7ba599_l3.png)
Reciprocal slopes
In any triangle in which two sides have reciprocal slopes, PROVE that equation (1) is satisfied.
Let ![]() be the common vertex from which the sides with reciprocal slopes originate. Let the two other vertices be
be the common vertex from which the sides with reciprocal slopes originate. Let the two other vertices be ![]() and
and ![]() . We have:
. We have:
![]()
Then
![Rendered by QuickLaTeX.com \begin{equation*} \begin{split} \frac{(\alpha_2-\alpha_1)^2+(\beta_2-\beta_1)^2}{(\alpha_3-\alpha_1)^2+(\beta_3-\beta_1)^2}&=\frac{(\alpha_2-\alpha_1)^2+\left[\frac{(\alpha_2-\alpha_1)(\alpha_3-\alpha_1)}{\beta_3-\beta_1}\right]^2}{(\alpha_3-\alpha_1)^2+(\beta_3-\beta_1)^2}\\ &=\frac{(\alpha_2-\alpha_1)^2}{(\beta_3-\beta_1)^2}\\ \left(\frac{(\alpha_2-\alpha_1)+(\beta_2-\beta_1)}{(\alpha_3-\alpha_1)+(\beta_3-\beta_1)}\right)^2&=\left(\frac{(\alpha_2-\alpha_1)+\left[\frac{(\alpha_2-\alpha_1)(\alpha_3-\alpha_1)}{\beta_3-\beta_1}\right]}{(\alpha_3-\alpha_1)+(\beta_3-\beta_1)}\right)^2\\ &=\left(\frac{\alpha_2-\alpha_1}{\beta_3-\beta_1}\right)^2 \end{split} \end{equation}](https://blog.fridaymath.com/wp-content/ql-cache/quicklatex.com-aeaa0450b46b497be3b8d72a5e62e89b_l3.png)
Favorite triangle:
Hardly would we talk about triangles without mentioning the ones we both cherish and relish — those whose slopes form geometric progressions. In today’s context, the ones with slopes ![]() satisfy equation (1).
satisfy equation (1).
Right triangles
PROVE that any right triangle satisfies equation (2).
Let ![]() ,
, ![]() , and
, and ![]() be the vertices of a right triangle, where
be the vertices of a right triangle, where ![]() is the vertex containing angle
is the vertex containing angle ![]() . We show that:
. We show that:
![]()
The proof is much like that of , with a slight modification.
Since the slopes of the sides originating from vertex ![]() are negative reciprocals of each other, we have:
are negative reciprocals of each other, we have:
![]()
Then
![Rendered by QuickLaTeX.com \begin{equation*} \begin{split} \frac{(\alpha_2-\alpha_1)^2+(\beta_2-\beta_1)^2}{(\alpha_3-\alpha_1)^2+(\beta_3-\beta_1)^2}&=\frac{(\alpha_2-\alpha_1)^2+\left[-\frac{(\alpha_2-\alpha_1)(\alpha_3-\alpha_1)}{\beta_3-\beta_1}\right]^2}{(\alpha_3-\alpha_1)^2+(\beta_3-\beta_1)^2}\\ &=\frac{(\alpha_2-\alpha_1)^2}{(\beta_3-\beta_1)^2}\\ \left(\frac{|\alpha_2-\alpha_1|+|\beta_2-\beta_1|}{|\alpha_3-\alpha_1|+|\beta_3-\beta_1|}\right)^2&=\left(\frac{|\alpha_2-\alpha_1|+\left |\left[-\frac{(\alpha_2-\alpha_1)(\alpha_3-\alpha_1)}{\beta_3-\beta_1}\right]\right |}{|\alpha_3-\alpha_1|+|\beta_3-\beta_1|}\right)^2\\ &=\left(\frac{\alpha_2-\alpha_1}{\beta_3-\beta_1}\right)^2 \end{split} \end{equation}](https://blog.fridaymath.com/wp-content/ql-cache/quicklatex.com-191fc21feb4ec99af19c12562fe0e8ac_l3.png)
In the end, only one of the four absolute values became absolutely valuable.
Let ![]() ,
, ![]() , and
, and ![]() . Using these values in the equation
. Using these values in the equation
![]()
the left side evaluates to the indeterminate form ![]() , while the right side is
, while the right side is ![]() . However, if we use absolute values on the left, then both sides evaluate to
. However, if we use absolute values on the left, then both sides evaluate to ![]() .
.
This is an exceptional case that happens whenever the slope of the line joining the points is ![]() . For this reason we generally recommend using equation (2).
. For this reason we generally recommend using equation (2).
Geometric application
The following shapes
- squares
- isosceles right triangles
- equilateral triangles with one side having slope of

- equilateral triangles with one side parallel to the
 -axis
-axis - isosceles triangles with one side parallel to the
 -axis
-axis
have something in common.
Let ![]() and
and ![]() be the endpoints of one diagonal of a square, and let
be the endpoints of one diagonal of a square, and let ![]() be any of the two remaining vertices. PROVE that
be any of the two remaining vertices. PROVE that ![]() .
.
Since a diagonal splits a square into two right triangles, we can apply equation (2):
![]()
noting that the right side evaluates to ![]() for our square. In turn:
for our square. In turn:
![]()
In view of the absolute values, we only take ![]() , which gives
, which gives ![]() .
.
In an equilateral triangle with one side parallel to the ![]() -axis, let
-axis, let ![]() be the “apex”, while
be the “apex”, while ![]() and
and ![]() are the two other vertices. PROVE that
are the two other vertices. PROVE that ![]() .
.
In such an equilateral triangle, the slopes of the sides are of the form ![]() . Since two of these are opposite values, we can use a previous example to deduce that equation (2) holds:
. Since two of these are opposite values, we can use a previous example to deduce that equation (2) holds:
![]()
The right side evaluates to ![]() for our equilateral triangle, so:
for our equilateral triangle, so:
![]()
In view of the absolute values, we only take ![]() , which gives
, which gives ![]() .
.
Takeaway
Out of the two equations we considered, we recommend the second one:
![]()
In practice, the equation works because of the ratio.
Tasks
- In any isosceles right triangle, PROVE that the equation
 holds, if
holds, if  is the vertex containing angle
is the vertex containing angle  , while
, while  and
and  are the other two vertices.
are the other two vertices. - Consider an equilateral triangle with vertices
 ,
,  , and
, and  . If the slope of side
. If the slope of side  is
is  , PROVE that:
, PROVE that:
- the slopes of sides
 and
and  are reciprocals of each other;
are reciprocals of each other;  .
.
- the slopes of sides
- Consider an equilateral triangle with vertices
 ,
,  , and
, and  . If the slope of side
. If the slope of side  is
is  , PROVE that:
, PROVE that:
- the slopes of sides
 and
and  are reciprocals of each other
are reciprocals of each other  .
.
- the slopes of sides
- Let
 be a right triangle in which
be a right triangle in which  is the point
is the point  and
and  . Side
. Side  makes angle
makes angle  with the positive
with the positive  -axis, and the lengths of
-axis, and the lengths of  and
and  are
are  and
and  , respectively. PROVE that one can describe:
, respectively. PROVE that one can describe:
 as the point
as the point 
 as the point
as the point  .
.
- Given a vertex
 , two side lengths
, two side lengths  and
and  , and a parameter
, and a parameter  :
:
- PROVE that any triangle with vertices
 ,
,  , and
, and  is a right triangle
is a right triangle - Using
 ,
,  ,
,  , and
, and  , verify that one obtains
, verify that one obtains  and
and  as the remaining two vertices.
as the remaining two vertices.
- PROVE that any triangle with vertices
- For
 , PROVE that any triangle with side slopes
, PROVE that any triangle with side slopes  is isosceles.
is isosceles. - Let
 ,
,  ,
,  , where
, where  , be the vertices of a triangle. PROVE that:
, be the vertices of a triangle. PROVE that:
- the triangle is isosceles
- the slopes of the sides form a geometric sequence with
 as common ratio
as common ratio - equation (2) is satisfied in this case.
- For a triangle with vertices
 ,
,  ,
,  , let
, let  ,
,  , and
, and  be the centroid, circumcenter, and orthocenter, respectively.
be the centroid, circumcenter, and orthocenter, respectively.
- calculate
 ,
,  , and
, and 
- verify that equation (2) is satisfied.
- calculate
- Suppose that an equilateral triangle has one side parallel to the
 -axis (so that its slope is undefined). PROVE that:
-axis (so that its slope is undefined). PROVE that:
- the slopes of the other two sides are opposites of each other
- equation (2) is satisfied.
- Given
 ,
,  , and
, and  :
:
- PROVE that any quadrilateral with vertices
 ,
,  ,
,  , and
, and  is a square
is a square - determine
 and
and  for the square with vertices
for the square with vertices  ,
,  ,
,  , and
, and  .
.
- PROVE that any quadrilateral with vertices