In conjunction with our newly found companion, whose name is Analytic Geometry, we wish you a happy new year!
Right now as we write, we’re situated right at the coordinates of the point where our interest intersects with this fine, familiar, friendly, fascinating companion.
And, today’s post stems from a task we asked you to do in the past. Our own solution sample yielded this post’s title, together with what we’ve assembled in the accompanying examples.
You’ll love this!!!
Example 1
Let ![]() be the
be the ![]() -coordinates of the vertices of a triangle. PROVE that the
-coordinates of the vertices of a triangle. PROVE that the ![]() -coordinate of the centroid is
-coordinate of the centroid is ![]() if, and only if, the sequence
if, and only if, the sequence ![]() is arithmetic.
is arithmetic.
Trivial fact presented in a technical way. Note that the result can be easily adapted for the ![]() -coordinates.
-coordinates.
To prove this, recall that the ![]() -coordinate of the centroid is the “average” of the
-coordinate of the centroid is the “average” of the ![]() -coordinates of the vertices of a triangle. In the present case we have
-coordinates of the vertices of a triangle. In the present case we have
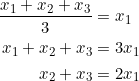
and so the sequence ![]() is arithmetic. Conversely, if the sequence
is arithmetic. Conversely, if the sequence ![]() is arithmetic, then
is arithmetic, then ![]() is the arithmetic mean of
is the arithmetic mean of ![]() and
and ![]() ; that is,
; that is, ![]() , which in turn gives
, which in turn gives ![]() . Add
. Add ![]() to both sides:
to both sides: ![]() , then divide both sides by
, then divide both sides by ![]() :
:
![]()
and so the ![]() -coordinate of the centroid is
-coordinate of the centroid is ![]() .
.
The next result can be combined with the above one to form three equivalent statements, but we’ve separated it for emphasis.
Example 2
Let ![]() be the
be the ![]() -coordinates of the vertices of a triangle. PROVE that the
-coordinates of the vertices of a triangle. PROVE that the ![]() -coordinate of the centroid is
-coordinate of the centroid is ![]() if, and only if, the median through the vertex containing
if, and only if, the median through the vertex containing ![]() is vertical.
is vertical.
First suppose that the ![]() -coordinate of the centroid is
-coordinate of the centroid is ![]() . From Example 1 above we saw that this means the sequence
. From Example 1 above we saw that this means the sequence ![]() is arithmetic, from which
is arithmetic, from which ![]() . Consider the diagram below:
. Consider the diagram below:
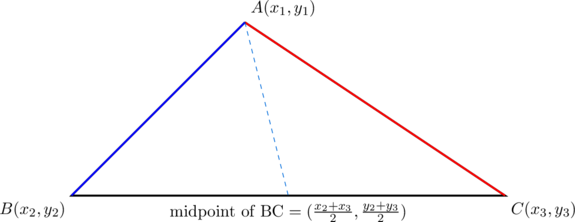
from which it can be seen that the median through ![]() goes through
goes through ![]() . Since
. Since ![]() , the median actually goes through
, the median actually goes through ![]() and
and ![]() , and so its equation is
, and so its equation is ![]() , a vertical line.
, a vertical line.
Conversely, if the equation of the median through vertex ![]() is
is ![]() , then the coordinates of the midpoint of the opposite side
, then the coordinates of the midpoint of the opposite side ![]() must satisfy this equation, giving
must satisfy this equation, giving ![]() which can be manipulated to obtain
which can be manipulated to obtain
![]()
and so the ![]() -coordinate of the centroid is
-coordinate of the centroid is ![]() .
.
Example 3
Let ![]() be the
be the ![]() -coordinates of the vertices of a triangle. PROVE that the
-coordinates of the vertices of a triangle. PROVE that the ![]() -coordinate of the centroid is
-coordinate of the centroid is ![]() if, and only if, the median through the vertex containing
if, and only if, the median through the vertex containing ![]() is horizontal.
is horizontal.
Since this is similar to Example 2, we omit the proof. Note that we used ![]() instead of
instead of ![]() here because of the next result.
here because of the next result.
Example 4
Let ![]() be the vertices of
be the vertices of ![]() . If the centroid is
. If the centroid is ![]() , PROVE that the slopes of the sides follow a geometric progression whose common ratio is
, PROVE that the slopes of the sides follow a geometric progression whose common ratio is ![]() .
.
Beautiful, colourful, simpleful, ![]() , whateverful that’s useful.
, whateverful that’s useful.
The slopes of the sides (![]() ), as seen from the diagram below
), as seen from the diagram below
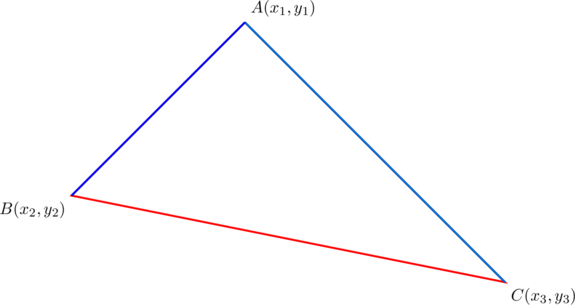
are:
![]()
respectively, and we assume that these expressions are well-behaved. We prove that the enumeration
(1) ![]()
is a geometric sequence and that its common ratio is ![]() .
.
Since the ![]() -coordinate of the centroid is
-coordinate of the centroid is ![]() , we have, by Example 1, that
, we have, by Example 1, that
(2) ![]()
Similarly, since the ![]() -coordinate of the centroid is
-coordinate of the centroid is ![]() , we have that
, we have that
(3) ![]()
Consider the second term of the enumeration in (1), namely ![]() . We have (by (2) and (3)) that:
. We have (by (2) and (3)) that:
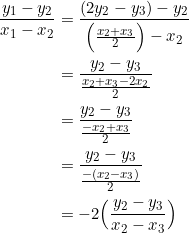
and so the second term in (1) is ![]() times the first. Now consider the third term, namely
times the first. Now consider the third term, namely ![]() . Again, by (2) and (3), we have that:
. Again, by (2) and (3), we have that:
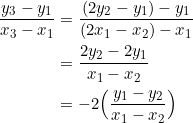
and so the third term is ![]() times the second. Therefore, the enumeration given by (1) is indeed a geometric sequence with a common ratio of
times the second. Therefore, the enumeration given by (1) is indeed a geometric sequence with a common ratio of ![]() .
.
The VHM property in triangles
By the VHM property, we mean that a triangle possesses a vertical median as well as a horizontal median (view the VHM property as a special case of two perpendicular medians).
Example 5
Give an example of a triangle that contains a vertical median and a horizontal median.
Easy. Very easy — as ![]() .
.
Indeed, the vertices of our triangle will be constructed from the numbers ![]() . Take
. Take ![]() with vertices
with vertices ![]() shown below:
shown below:
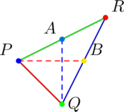
Notice the horizontal median ![]() and the vertical median
and the vertical median ![]() . Also, the slope of
. Also, the slope of ![]() is
is ![]() ; the slope of
; the slope of ![]() is
is ![]() ; the slope of
; the slope of ![]() is
is ![]() . Re-arranging, we have the geometric sequence of slopes:
. Re-arranging, we have the geometric sequence of slopes:
![]()
The common ratio is ![]() as you’ve seen. Also worth noting is that the above triangle is isosceles; in the next example, we show that not all VHM triangles are isosceles.
as you’ve seen. Also worth noting is that the above triangle is isosceles; in the next example, we show that not all VHM triangles are isosceles.
Example 6
Give an example of a scalene triangle that contains a vertical median and a horizontal median.
Consider ![]() shown below:
shown below:
![]() so this triangle is scalene. Its centroid is located at
so this triangle is scalene. Its centroid is located at ![]() , the median
, the median ![]() is vertical, while the median
is vertical, while the median ![]() is horizontal. Moreover, the slopes of sides
is horizontal. Moreover, the slopes of sides ![]() are
are ![]() respectively. They form a geometric sequence whose common ratio is
respectively. They form a geometric sequence whose common ratio is ![]() , as you know.
, as you know.
Example 7
Find a general set of coordinates for the vertices of a triangle that satisfies the VHM property.
Let ![]() and
and ![]() be real numbers. Set
be real numbers. Set
![]()
Then ![]() satisfies the VHM property. Indeed, its centroid is located at
satisfies the VHM property. Indeed, its centroid is located at
![]()
and so it shares an ![]() -coordinate with vertex
-coordinate with vertex ![]() and a
and a ![]() -coordinate with vertex
-coordinate with vertex ![]() . By Example 2 and Example 3, it contains a vertical median and a horizontal median, which is the VHM property.
. By Example 2 and Example 3, it contains a vertical median and a horizontal median, which is the VHM property.
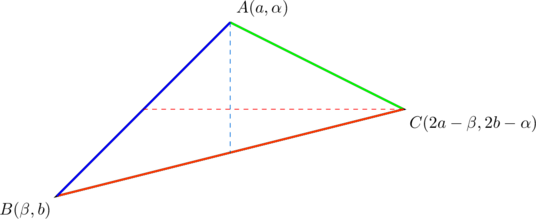
Notice that the slopes of sides ![]() are
are
![]()
respectively. These slopes form a geometric progression with a common ratio of ![]() , as expected. Note that it is important to impose the restrictions
, as expected. Note that it is important to impose the restrictions ![]() and
and ![]() .
.
Example 8
PROVE that if a triangle contains a vertical median and a horizontal median, then the product of the slopes of the sides is a “perfect cube”.
The slopes of the sides of a VHM triangle were calculated in Example 7; their product is
![]()
which is a “perfect cube”. (We’ve used the term “perfect cube” in a loose way here.)
A VHM triangle contains a vertical median (undefined slope) and a horizontal median (zero slope). The remaining “non-degenerate” median has a slope that’s related to the slope of the side it meets.
Example 9
PROVE that the slope of the “non-degenerate” median in a VHM triangle is the negative of the slope of the side that contains its foot.
Consider the “non-degenerate” median (dashed blue line) in the diagram below:
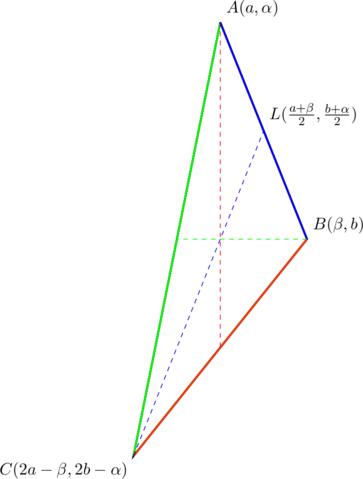
The slope of side ![]() is
is ![]() . Let’s calculate the slope of median
. Let’s calculate the slope of median ![]() :
:
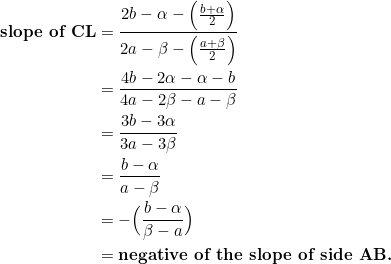
We’ve saved the last for last (you read that correctly), which has to do with the converse of what we saw in Example 4.
Example 10
PROVE that if the slopes of the sides of a triangle form a geometric progression with a common ratio of ![]() , then the triangle contains a vertical median and a horizontal median.
, then the triangle contains a vertical median and a horizontal median.
Beautiful, colourful, ![]() , whateverful.
, whateverful.
Let ![]() be the vertices of a triangle whose sides slopes form a geometric progression with a common ratio of
be the vertices of a triangle whose sides slopes form a geometric progression with a common ratio of ![]() . Enumerate this geometric progression as
. Enumerate this geometric progression as
![]()
and let the terms correspond, respectively, to the slopes of sides ![]() . Then we have the following linear system:
. Then we have the following linear system:
(4) ![]()
(5) ![]()
(6) ![]()
This is a homogeneous linear system that is underdetermined (it contains fewer equations than unknowns). By a result in linear algebra, such a system always has non-trivial solutions. In fact, our solution is:
![]()
Note that ![]() have been expressed in terms of
have been expressed in terms of ![]() because the system given by (4), (5),(6) has three degrees of freedom. Don’t worry about these technical terms. The centroid of
because the system given by (4), (5),(6) has three degrees of freedom. Don’t worry about these technical terms. The centroid of ![]() is
is
![]()
after simplification. Since the centroid shares an ![]() -coordinate with vertex
-coordinate with vertex ![]() and a
and a ![]() -coordinate with vertex
-coordinate with vertex ![]() , it contains a vertical median and a horizontal median.
, it contains a vertical median and a horizontal median.
It follows that a triangle satisfies the VHM property if, and only if, the slopes of its sides form a geometric progression whose common ratio is ![]() .
.
Takeaway
The centroid of a triangle is properly located within the triangle (unlike the circumcenter or orthocenter that are sometimes situated outside). The centroid hardly “shares” its coordinates with any of the triangle’s vertices, but when it does decide to share, then it “straightens” one median and “flattens” the other.
Tasks
- Let
 be an arithmetic sequence, and let
be an arithmetic sequence, and let  be another arithmetic sequence. PROVE that the points
be another arithmetic sequence. PROVE that the points  lie on a straight line.
lie on a straight line.
 This shows that, in order to form a triangle, the order in which we select coordinates from the sequences matter.
This shows that, in order to form a triangle, the order in which we select coordinates from the sequences matter.
- PROVE that an equilateral triangle can never contain a vertical median and a horizontal median at the same time.
- PROVE that if a right triangle is to contain both a vertical median and a horizontal median simultaneously, then the slopes of its sides have to be
 , or
, or  .
.
(Further, the medians to the two legs cannot be vertical and horizontal at the same time.) - Suppose that
 contains a vertical median and a horizontal median. PROVE that if one of its sides has a slope of
contains a vertical median and a horizontal median. PROVE that if one of its sides has a slope of  , then
, then  is isosceles.
is isosceles. - Suppose that
 contains a vertical and a horizontal median. PROVE that the sum of the slopes of its sides is
contains a vertical and a horizontal median. PROVE that the sum of the slopes of its sides is  times the slope which is the geometric mean of the other two slopes.
times the slope which is the geometric mean of the other two slopes.
 For such a triangle, the slopes of the sides form a geometric sequence with a common ratio of
For such a triangle, the slopes of the sides form a geometric sequence with a common ratio of  , so it makes sense to talk about the “geometric mean” of the slopes.
, so it makes sense to talk about the “geometric mean” of the slopes. 
- PROVE that if a triangle contains a vertical and a horizontal median, then the sum of product of the slopes of the sides, taken two at a time, is always negative.
- The three medians of a triangle divide the triangle into six smaller triangles of equal areas. PROVE that if the original triangle satisfies the VHM property, then two out of the six smaller triangles are right triangles. If, in addition, the original triangle is isosceles and satisfies the VHM property, PROVE that four out of the six smaller triangles are right triangles.
- Let
 be the coordinates of
be the coordinates of  . PROVE
. PROVE  .
.
 This triangle contains a vertical median and a horizontal median, so the above equation is an instance of a well-known result; see this article.
This triangle contains a vertical median and a horizontal median, so the above equation is an instance of a well-known result; see this article. 
- Let
 be the coordinates of
be the coordinates of  . PROVE that its area is
. PROVE that its area is  .
.
 Note that this triangle contains a vertical median and a horizontal median, and so its area takes a simple form.
Note that this triangle contains a vertical median and a horizontal median, and so its area takes a simple form. 
- Let
 be the coordinates of
be the coordinates of  . PROVE that the slope of its Euler line can be given by
. PROVE that the slope of its Euler line can be given by 
2 thoughts on “Vertical and horizontal medians”
Comments are closed.