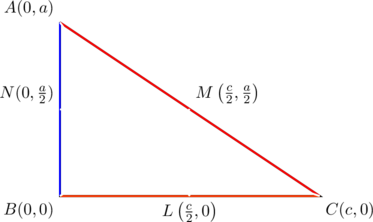
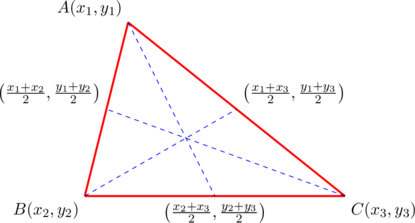
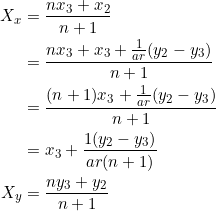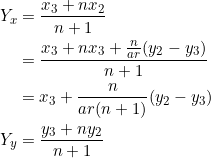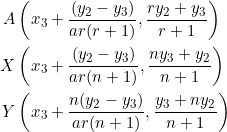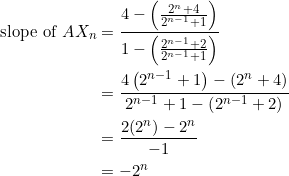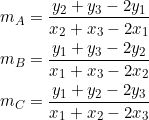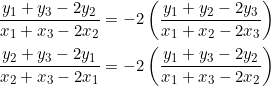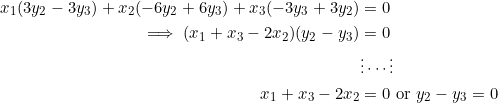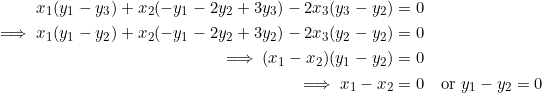Let ![]() be lengths of the sides of a triangle, and let the slopes of these sides be
be lengths of the sides of a triangle, and let the slopes of these sides be ![]() , respectively. Then, as we show in example 10:
, respectively. Then, as we show in example 10:
(1) ![]()
This is analogous to the Pythagorean identity for right triangles. In theory, if we let ![]() (or
(or ![]() ), then
), then ![]() . Thus, in a sense, a right triangle is a limiting case of a triangle with slopes in geometric progression.
. Thus, in a sense, a right triangle is a limiting case of a triangle with slopes in geometric progression.
Whatever a right triangle can do: 
Whatever a right triangle can “do”, there is a triangle with slopes ![]() that can “do” the same thing. Did we just exaggerate?
that can “do” the same thing. Did we just exaggerate?
Compare the hypotenuse of a right triangle with side ![]() of a triangle whose slopes are
of a triangle whose slopes are ![]() .
.
By side ![]() , we mean the side whose slope is
, we mean the side whose slope is ![]() , the geometric mean of the progression
, the geometric mean of the progression ![]() .
.
- In terms of length: If
 , then (in view of (1)) the side with length
, then (in view of (1)) the side with length  is the longest side of the triangle, just like the hypotenuse of a right triangle.
is the longest side of the triangle, just like the hypotenuse of a right triangle.
(Winner: Right triangle — because it always satisfies this property; our own triangle doesn’t always satisfy it if .)
.) - The median to the hypotenuse: In a right triangle, the length of the median to the hypotenuse is always half of the length of the hypotenuse. In a triangle with slopes
 , the length of the median to side
, the length of the median to side  has length
has length  (See the exercises). And so as
(See the exercises). And so as  , this becomes
, this becomes  .
.
(Winner: Right triangle again — because it always satisfies this property, while our own triangle satisfies it only when .)
.) - Slope of the median to the hypotenuse: If the legs of a right triangle are parallel to the coordinate axes, then the slope of the median to the hypotenuse is the negative of the slope of the hypotenuse. On the other hand, in a triangle with slopes
 , the slope of the median to side
, the slope of the median to side  is always the negative of the slope of side
is always the negative of the slope of side  .
.
(Winner: The triangle with slopes wins here — because it always satisfies this property, whereas a right triangle satisfies it only when its legs are parallel to the coordinate axes.)
wins here — because it always satisfies this property, whereas a right triangle satisfies it only when its legs are parallel to the coordinate axes.)
Final Score: Right triangle won ![]() to
to ![]() — courtesy of our generosity.
— courtesy of our generosity.
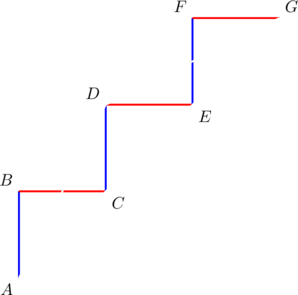
Consider ![]() with vertices
with vertices ![]() ,
, ![]() , and
, and ![]() . Verify that the side lengths satisfy equation (1).
. Verify that the side lengths satisfy equation (1).
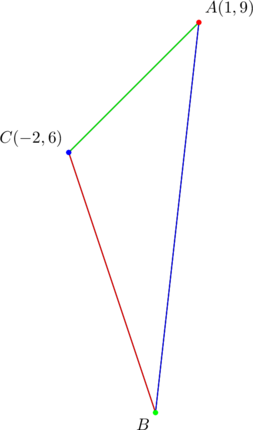
Observe that the slopes are ![]() for sides
for sides ![]() , respectively. They form a geometric progression in which
, respectively. They form a geometric progression in which ![]() .
.
In (1), the side with length ![]() is the side whose slope is the geometric mean of the progression — in the present case, it is side
is the side whose slope is the geometric mean of the progression — in the present case, it is side ![]() . This is important.
. This is important. ![]() and
and ![]() can then be chosen as the lengths of the other two sides.
can then be chosen as the lengths of the other two sides.
Using the given vertices ![]() , let’s compute the side lengths:
, let’s compute the side lengths:
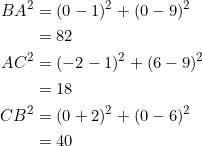
Since ![]() , we have to take
, we have to take ![]() . Let
. Let ![]() and let
and let ![]() . Then:
. Then:
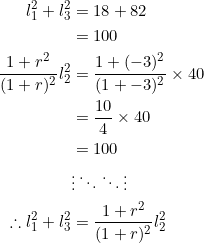
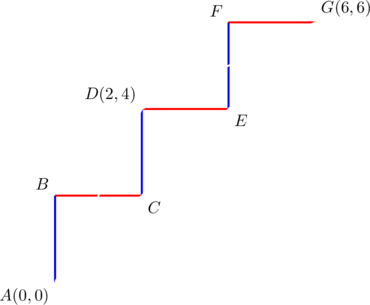
Consider ![]() with vertices
with vertices ![]() ,
, ![]() , and
, and ![]() . Verify that the side lengths satisfy equation (1).
. Verify that the side lengths satisfy equation (1).
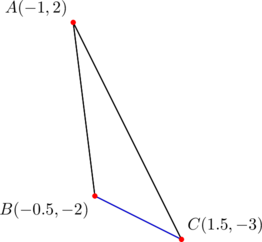
The slopes of sides ![]() are
are ![]() , respectively. They form a geometric progression with common ratio
, respectively. They form a geometric progression with common ratio ![]() . Further, the slope of side
. Further, the slope of side ![]() , namely
, namely ![]() , is the geometric mean of the progression. Thus the length of side
, is the geometric mean of the progression. Thus the length of side ![]() will be taken as
will be taken as ![]() in (1).
in (1).
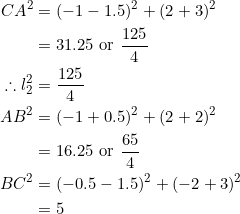
Since ![]() has been chosen as
has been chosen as ![]() , we can take
, we can take ![]() and
and ![]() . Then, in (1):
. Then, in (1):
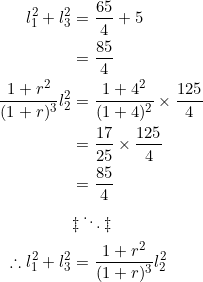
So the formula works for both negative and positive common ratios.
The slopes of the sides of ![]() are all non-zero and the side lengths satisfy
are all non-zero and the side lengths satisfy ![]() . Find possible coordinates for the vertices
. Find possible coordinates for the vertices ![]() .
.
The only challenge here is the non-zero slope specification; otherwise, we could just place two vertices along the ![]() -axis, making the third vertex easy to find.
-axis, making the third vertex easy to find.
Fortunately, we can always appeal to triangles whose slopes form geometric progressions under this situation. They’re cut out for these.
In (1), set ![]() and solve for
and solve for ![]() :
:
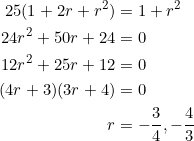
The workload now reduces to finding coordinates for a triangle whose slopes form a geometric progression in which ![]() .
.
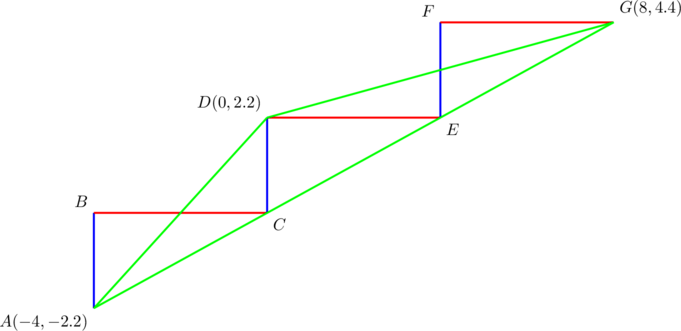
Easy-peasy. We can use ![]() ,
, ![]() ,
, ![]() and just put
and just put ![]() .
.
We obtain ![]() ,
, ![]() , and
, and ![]() . The side slopes are all non-zero:
. The side slopes are all non-zero: ![]() ,
, ![]() , and
, and ![]() .
.
For the side lengths, we have:
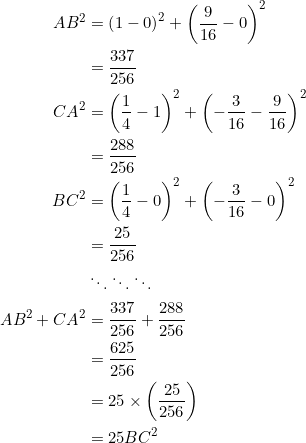
DONE!!! ![]() , with
, with ![]() ,
, ![]() , and
, and ![]() .
.
Quantity digression
Let’s examine the quantity ![]() that appeared in formula (1).
that appeared in formula (1).
For real ![]() , PROVE that the minimum value of
, PROVE that the minimum value of ![]() is
is ![]() .
.
Let’s do this for real. And, without using calculus. Set ![]() and clear fractions to obtain
and clear fractions to obtain ![]() .
.
(2) 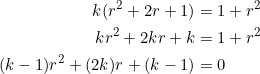
Now comes the main point. Since ![]() is a real number, the discriminant of the above quadratic must be greater than or equal to zero. So:
is a real number, the discriminant of the above quadratic must be greater than or equal to zero. So:
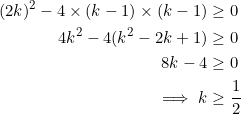
Thus, ![]() .
.
Let ![]() be an integer. PROVE that
be an integer. PROVE that ![]() is also an integer if and only if
is also an integer if and only if ![]() .
.
If you’ve been following our posts, you may have noticed our public, profuse admiration for ![]() . It is a peach.
. It is a peach.
Put ![]() to obtain
to obtain ![]() ; put
; put ![]() to get
to get ![]() .
.
Conversely, suppose that ![]() is an integer, with
is an integer, with ![]() an integer too. We’ll show that
an integer too. We’ll show that ![]() must be
must be ![]() or
or ![]() . Set
. Set ![]() , then we obtain what we had in (2):
, then we obtain what we had in (2):
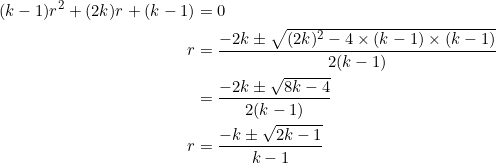
To obtain an integer solution, the quantity under the square root, namely ![]() , must first of all be a perfect square. Since
, must first of all be a perfect square. Since ![]() is an odd number, it must be congruent to
is an odd number, it must be congruent to ![]() modulo
modulo ![]() if it’s a perfect square (a bit of number theory here
if it’s a perfect square (a bit of number theory here ![]() no worries
no worries ![]() ). Basically, the difference
). Basically, the difference ![]() must be divisible by
must be divisible by ![]() .
.
Continuing, let’s set ![]() , for some integer
, for some integer ![]() . As this leads to
. As this leads to ![]() , we obtain
, we obtain ![]() . Using this in the expression we obtained for
. Using this in the expression we obtained for ![]() :
:
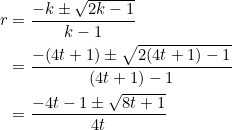
Now ![]() is a perfect square if and only if
is a perfect square if and only if ![]() for some positive integer
for some positive integer ![]() (see the exercises at the end). Thus we have
(see the exercises at the end). Thus we have
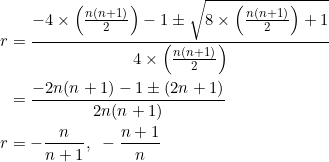
Consider ![]() . It is an integer only when
. It is an integer only when ![]() — giving
— giving ![]() , respectively.
, respectively.
Consider ![]() . It is an integer only when
. It is an integer only when ![]() . Put
. Put ![]() to obtain
to obtain ![]() . (Using
. (Using ![]() gives
gives ![]() again. However, because of the discriminant of the quadratic equation we solved, we don’t want
again. However, because of the discriminant of the quadratic equation we solved, we don’t want ![]() . Similarly, we don’t want
. Similarly, we don’t want ![]() above.)
above.)
Our decision to follow a longer procedure is that it also yields the form of rational numbers — not just integers — that make the expression ![]() an integer.
an integer.
If a right triangle satisfies (1), PROVE that the side whose length is ![]() cannot be the hypotenuse.
cannot be the hypotenuse.
We can use slopes to do this, but let’s use lengths instead.
Suppose the length of the hypotenuse is ![]() . Then we have
. Then we have ![]() by the Pythagorean theorem. Together with (1) we have the following quadratic-quadratic system:
by the Pythagorean theorem. Together with (1) we have the following quadratic-quadratic system:
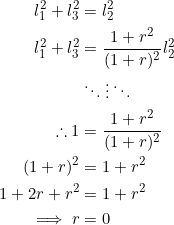
Since ![]() is not allowed for a geometric progression, we conclude that
is not allowed for a geometric progression, we conclude that ![]() cannot be the hypotenuse.
cannot be the hypotenuse.
The peach of the bunch
Any triangle whose slopes form a geometric sequence with common ratio ![]() is a peach. If it’s also a right triangle, then it becomes the peach of the pick of the bunch.
is a peach. If it’s also a right triangle, then it becomes the peach of the pick of the bunch.
If a right triangle has ![]() , PROVE that the
, PROVE that the ![]() -coordinates, the
-coordinates, the ![]() -coordinates, and the squares of the lengths form arithmetic progressions.
-coordinates, and the squares of the lengths form arithmetic progressions.
Our first post of this year showed that if ![]() , then the
, then the ![]() -coordinates and the
-coordinates and the ![]() -coordinates form (different) arithmetic progressions — even when the triangle is not right.
-coordinates form (different) arithmetic progressions — even when the triangle is not right.
Put ![]() in (1) to obtain
in (1) to obtain
![]()
By the way, this is a well-known condition for perpendicular medians.
Since we’re dealing with a right triangle this time (and ![]() cannot be the hypotenuse, in view of the previous example), we can take
cannot be the hypotenuse, in view of the previous example), we can take ![]() as the hypotenuse, so that
as the hypotenuse, so that
![]()
Eliminate ![]() from the two equations:
from the two equations: ![]() .
.
Then ![]() .
.
The squares of the lengths, in terms of ![]() , are:
, are: ![]() . They form an arithmetic sequence.
. They form an arithmetic sequence.
If a right triangle has ![]() , PROVE that
, PROVE that ![]() , or
, or ![]() .
.
Assume the progression of the slopes is ![]() . If
. If ![]() , then this becomes
, then this becomes ![]() .
.
We must have ![]() .
.
Or we must have ![]() .
.
Derivation of the formula
We now derive equation (1).
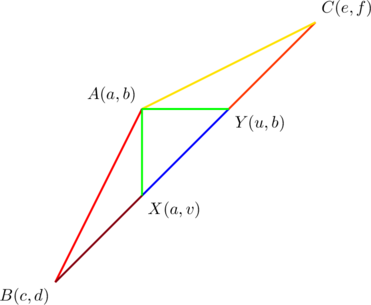
In ![]() , let
, let ![]() be the slopes of sides
be the slopes of sides ![]() , respectively. If the lengths of these sides are also denoted by
, respectively. If the lengths of these sides are also denoted by ![]() , PROVE that
, PROVE that ![]() .
.
Let the vertices be ![]() . Then the following relations exist among the coordinates:
. Then the following relations exist among the coordinates:
(3) 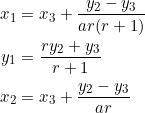
Using the distance formula:
![Rendered by QuickLaTeX.com \begin{equation*} \begin{split} l_1^2&=AB^2\\ &=\left[x_3+\frac{y_2-y_3}{ar(r+1)}-\left(x_3+\frac{y_2-y_3}{ar}\right)\right]^2+\left[\frac{ry_2+y_3}{r+1}-y_2\right]^2\\ &=\left(-\frac{y_2-y_3}{a(r+1)}\right)^2+\left(-\frac{y_2-y_3}{r+1}\right)^2\\ &=\left(\frac{a^2+1}{a^2(r+1)^2}\right)(y_2-y_3)^2\\ l_2^2&=BC^2\\ &=\left(\frac{a^2r^2+1}{a^2r^2}\right)(y_2-y_3)^2\\ l_3^2&=CA^2\\ &=\left(\frac{a^2r^4+1}{a^2r^2(r+1)^2}\right)(y_2-y_3)^2\\ &\ddots\ddots\ddots\\ &\ddots\ddots\ddots\\ l_1^2+l_3^2&=\left(\frac{a^2+1}{a^2(r+1)^2}\right)(y_2-y_3)^2+\left(\frac{a^2r^4+1}{a^2r^2(r+1)^2}\right)(y_2-y_3)^2\\ &=\frac{(r^2+1)(a^2r^2+1)}{a^2r^2(r+1)^2}(y_2-y_3)^2\\ \frac{r^2+1}{(r+1)^2}l_2^2&=\frac{r^2+1}{(r+1)^2}\times\left(\frac{a^2r^2+1}{a^2r^2}\right)(y_2-y_3)^2\\ &=\frac{(r^2+1)(a^2r^2+1)}{a^2r^2(r+1)^2}(y_2-y_3)^2\\ &=l_1^2+l_3^2\\ &\ddots\ddots\ddots\ddots\ddots\ddots\ddots\\ &\ddots\ddots\ddots\ddots\ddots\ddots\ddots\\ \therefore l_1^2+l_3^2&=\frac{r^2+1}{(r+1)^2}l_2^2. \end{split} \end{equation*}](https://blog.fridaymath.com/wp-content/ql-cache/quicklatex.com-8c03ccf870afb9a58be454921b06263b_l3.png)
Takeaway
In the equation
![]()
the side whose length is ![]() plays a crucial role in the theory of triangles with slopes
plays a crucial role in the theory of triangles with slopes ![]() . In particular, it acts like the hypotenuse of a right triangle.
. In particular, it acts like the hypotenuse of a right triangle.
(For something totally irrelevant, we would like to point out that the title of this post — approximate pythagorean identity — reminds us of APIs, a truly endearing term in programming that abbreviates Application Programming Interface. We lve APIs!!!!!!!!!!)
Tasks
- (Number theory) A triangle has non-zero side slopes, and its side lengths
 are related via
are related via  . Find possible coordinates for the vertices of the triangle.
. Find possible coordinates for the vertices of the triangle.
(Observe that . And, in our example, we had
. And, in our example, we had  . The quantity
. The quantity  that appeared in (1) is always a sum of two consecutive squares, if it is an integer. But it is not always a perfect square. Thus, this closely relates to a problem in number theory where integer solutions to equations of the form
that appeared in (1) is always a sum of two consecutive squares, if it is an integer. But it is not always a perfect square. Thus, this closely relates to a problem in number theory where integer solutions to equations of the form  are sought.)
are sought.) - For
 , PROVE that
, PROVE that  .
. - Let
 . PROVE that
. PROVE that  is an integer if and only if
is an integer if and only if  is of the form
is of the form  or
or  , for some (positive) integer
, for some (positive) integer  .
. - Let
 . PROVE that the integer values of
. PROVE that the integer values of  are always of the form
are always of the form  .
. - PROVE that the roots of the quadratic equation
 are reciprocals of each other.
are reciprocals of each other.
(Alternatively, this means that if , then both
, then both  and
and  yield the same values for the quantity
yield the same values for the quantity  .)
.) - Let
 be an integer. PROVE that
be an integer. PROVE that  is a perfect square if and only if
is a perfect square if and only if  for some (positive) integer
for some (positive) integer  .
. - (Quadratic proximity) Let
 be the slopes of the sides of a triangle.
be the slopes of the sides of a triangle.
- If the triangle is right isosceles, PROVE that
 ;
; - If the triangle is equilateral, PROVE that
 .
.
- If the triangle is right isosceles, PROVE that
- In
 , let sides
, let sides  have slopes
have slopes  , respectively. PROVE that
, respectively. PROVE that  , where
, where  is the length of the median from vertex
is the length of the median from vertex  and
and  is the length of side
is the length of side  .
.
(In particular, when , we obtain
, we obtain  , ignoring the negative sign. Thus, the length of the median to side
, ignoring the negative sign. Thus, the length of the median to side  is half the length of
is half the length of  , similar to the median to the hypotenuse in a right triangle. But
, similar to the median to the hypotenuse in a right triangle. But  is not allowed here.)
is not allowed here.) - Let
 .
.
- If
 , PROVE that
, PROVE that  .
. - If
 , PROVE that
, PROVE that  if and only if
if and only if  .
. - If
 , PROVE that
, PROVE that  if and only if
if and only if  has the form
has the form  or
or  for some integer
for some integer  .
.
- If
- Find exact solutions to the equation
 .
.
(Later on we’ll show how appears in median lengths of triangles with slopes in geometric progression.)
appears in median lengths of triangles with slopes in geometric progression.)
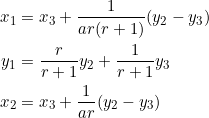
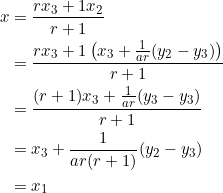
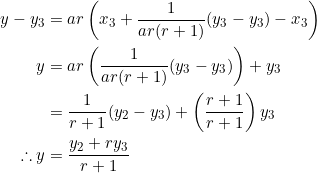
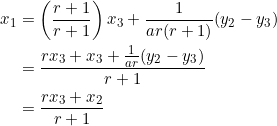
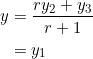
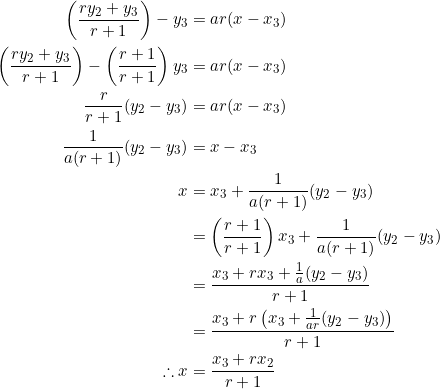
![Rendered by QuickLaTeX.com \begin{equation*} \begin{split} (a-c)^2+(v-d)^2&=\left[(e-u)\left(\frac{v-d}{a-c}\right)\right]^2+(e-u)^2\\ (a-c)^2+(v-d)^2&=(e-u)^2\left[\frac{(v-d)^2+(a-c)^2}{(a-c)^2}\right]\\ \therefore (a-c)^2&=(e-u)^2 \end{split} \end{equation*}](https://blog.fridaymath.com/wp-content/ql-cache/quicklatex.com-9d118a4597d95d6a517f8713561f7ae7_l3.png)
![Rendered by QuickLaTeX.com \begin{equation*} \begin{split} \left(\frac{f-d}{e-c}\right)^2&=\left(\frac{b-v}{u-a}\right)^2\\ \left(\frac{f-b}{e-a}\right)\left(\frac{b-d}{a-c}\right)&=\left[(e-u)\frac{b-v}{u-a}\right].\frac{1}{e-a}\left(\frac{b-d}{a-c}\right)\\ &=\left(\frac{b-v}{u-a}\right)\left(\frac{b-d}{e-a}\right)\\ &=\left(\frac{b-v}{u-a}\right)\left(\frac{b-d}{u-c}\right)\\ &=\left(\frac{b-v}{u-a}\right)\left(\frac{b-v}{u-a}\right) \end{split} \end{equation*}](https://blog.fridaymath.com/wp-content/ql-cache/quicklatex.com-3a905b562287039a1b71d82b26339bf8_l3.png)