Equivalently, two radii are parallel to two sides of the parent triangle, as will be shown in examples 1 and 2 below.
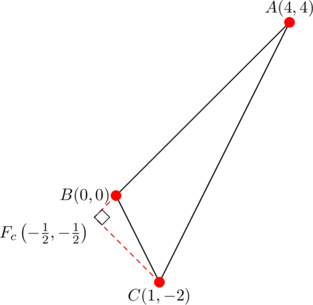
Everything we’ve been considering so far seems to work smoothly for the ![]() -triangle.
-triangle.
Since the parent triangle is obtuse, its circumcenter ![]() lies outside, opposite the obtuse angle. Thus
lies outside, opposite the obtuse angle. Thus ![]() is a (convex) quadrilateral.
is a (convex) quadrilateral.
If ![]() is the radius of the circumcircle of triangle
is the radius of the circumcircle of triangle ![]() , then we have that
, then we have that ![]() and
and ![]() (see here). Since
(see here). Since ![]() is the circumcenter, we also have that
is the circumcenter, we also have that ![]() . Hence,
. Hence, ![]() is a rhombus; in fact, a special rhombus with the property that the diagonal
is a rhombus; in fact, a special rhombus with the property that the diagonal ![]() is equal to the equal sides. Every rhombus is a parallelogram so we conclude that radius
is equal to the equal sides. Every rhombus is a parallelogram so we conclude that radius ![]() is parallel to side
is parallel to side ![]() and radius
and radius ![]() is parallel to side
is parallel to side ![]() .
.
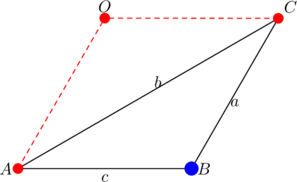
Suppose that a triangle ![]() with circumcenter
with circumcenter ![]() has the property that radius
has the property that radius ![]() is parallel to side
is parallel to side ![]() and radius
and radius ![]() is parallel to side
is parallel to side ![]() . Such a triangle is necessarily obtuse, so that the circumcenter
. Such a triangle is necessarily obtuse, so that the circumcenter ![]() lies outside the triangle and we again have a quadrilateral
lies outside the triangle and we again have a quadrilateral ![]() . Join
. Join ![]() and let
and let ![]() . Since
. Since ![]() is parallel to
is parallel to ![]() , we have that
, we have that ![]() . Since
. Since ![]() is the circumcenter, triangle
is the circumcenter, triangle ![]() is isosceles and so
is isosceles and so ![]() . The situation is shown below, with the circumcircle included:
. The situation is shown below, with the circumcircle included:
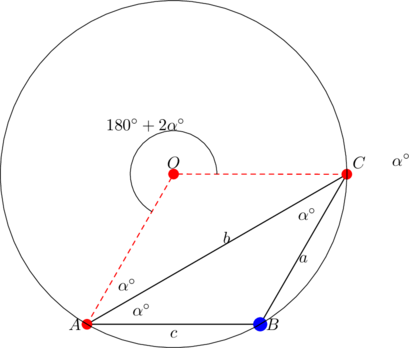
Since ![]() is parallel to
is parallel to ![]() , we have that
, we have that ![]() . Thus, triangle
. Thus, triangle ![]() is isosceles; moreover,
is isosceles; moreover, ![]() . By the inscribed angle theorem:
. By the inscribed angle theorem:
![]()
Thus, the interior angles of triangle ![]() are
are ![]() and
and ![]() .
.
Since the area satisfies ![]() , we have that
, we have that ![]() .
.
Normally, ![]() . And so we must have
. And so we must have ![]() . In turn, this implies
. In turn, this implies
![]()
![]() is not possible due to the fact that
is not possible due to the fact that ![]() and
and ![]() . So we take
. So we take ![]() , which yields
, which yields ![]() . Using
. Using ![]() we get
we get
![]()
Consequently, ![]() .
.
No matter how the vertices are arranged, we’ll end up with a rhombus in which a diagonal is equal to the side-lengths. The interior angles of such a rhombus are ![]() . Now just consider the triangle that remains when
. Now just consider the triangle that remains when ![]() is removed.
is removed.
Consider various arrangements of the rhombus ![]() , for example the one shown below:
, for example the one shown below:

Apply the inscribed angle theorem to see that it is not possible to have ![]() be a square.
be a square.
Takeaway
In any triangle ![]() , let
, let ![]() be the side-lengths,
be the side-lengths, ![]() the orthocenter,
the orthocenter, ![]() the circumcenter, and
the circumcenter, and ![]() the circumradius. Then the following statements are equivalent:
the circumradius. Then the following statements are equivalent:


- the reflection of
 over
over  is
is 
- the area
 satisfies
satisfies 
- the reflection of
 over
over  is
is  and the reflection of
and the reflection of  over
over  is
is 
Task
- (Aufbau) In triangle
 , let
, let  be the side-lengths,
be the side-lengths,  the circumradius,
the circumradius,  the circumcenter,
the circumcenter,  the nine-point center, and
the nine-point center, and  the orthocenter. PROVE that the following statements are equivalent:
the orthocenter. PROVE that the following statements are equivalent:



- the reflection of
 over
over  is
is 
- the area
 satisfies
satisfies 
- the circle with diameter
 passes through vertices
passes through vertices  and
and 
- radius
 is parallel to side
is parallel to side  and radius
and radius  is parallel to side
is parallel to side 
- the reflection of
 over
over  is
is  and the reflection of
and the reflection of  over
over  is
is 
 is the geometric mean of
is the geometric mean of  and
and  , and
, and  is the geometric mean of
is the geometric mean of  and
and  . (
. ( and
and  are the feet of the altitudes from
are the feet of the altitudes from  and
and  , respectively.)
, respectively.)