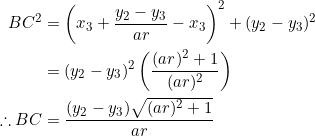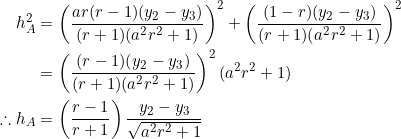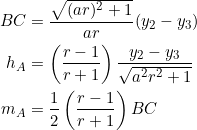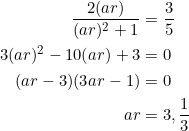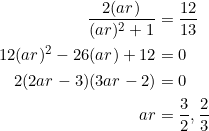We’re getting close to reaching (part of) our goal of having a clone of the right triangle, as this equation shows:
(1) ![]()
Ve![]() y close. Ve
y close. Ve![]() y close. Ve
y close. Ve![]() y close.
y close.
Succinct strategy
In ![]() , let
, let ![]() be the slopes of sides
be the slopes of sides ![]() . Let
. Let ![]() be the lengths of the altitudes from each vertex. We’ll derive equation (1) in two ways: The first approach is straight-forward, utilizing a previous post and a fact from this site, namely
be the lengths of the altitudes from each vertex. We’ll derive equation (1) in two ways: The first approach is straight-forward, utilizing a previous post and a fact from this site, namely
(2) ![]()
where ![]() is the radius of the circumcircle of
is the radius of the circumcircle of ![]() and
and ![]() are the side-lengths. The second method is long-winded, painstaking, old-fashioned.
are the side-lengths. The second method is long-winded, painstaking, old-fashioned.
Example 1
In any ![]() , PROVE that
, PROVE that ![]() .
.
Using equation (2), we have:
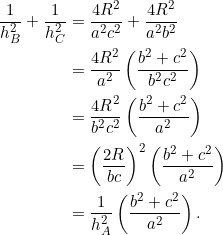
It follows immediately that in a right triangle with ![]() we have
we have
![]()
Example 2
![]()
holds in a ![]() with
with ![]() as the slopes of sides
as the slopes of sides ![]() .
.
We use an identity from one of our previous posts, namely
![]()
In terms of the standard notation, this is the same as ![]() . Or:
. Or:
![]()
In view of example 1, we then have:
![]()
Point-blank.
Verbose verification
In ![]() with slopes
with slopes ![]() for sides
for sides ![]() , find the length of the altitude from vertex
, find the length of the altitude from vertex ![]() . Take
. Take ![]() ,
, ![]() ,
, ![]() .
.
The length of the altitude from vertex ![]() is
is
![]()
(Absolute values may be necessary. Also notice how we switched the slopes from ![]() to
to ![]() .)
.)
In ![]() with slopes
with slopes ![]() for sides
for sides ![]() , find the length of the altitude from vertex
, find the length of the altitude from vertex ![]() . Take
. Take ![]() ,
, ![]() ,
, ![]() .
.
It is:
![]()
(Again, absolute values may be necessary.)
In ![]() with slopes
with slopes ![]() for sides
for sides ![]() , find the length of the altitude from vertex
, find the length of the altitude from vertex ![]() . Take
. Take ![]() ,
, ![]() ,
, ![]() .
.
It is:
![]()
(Absolute values may be necessary.)
From examples 3,4,5 we had:
![]()
Thus:
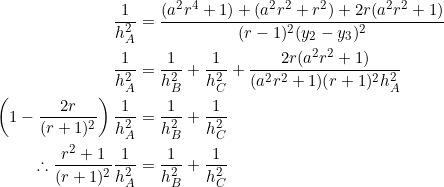
The slopes of sides ![]() are
are ![]() , respectively. They form a geometric progression in which
, respectively. They form a geometric progression in which ![]() . As per our arrangement, we’ll take
. As per our arrangement, we’ll take ![]() and
and ![]() . Therefore the three altitudes are:
. Therefore the three altitudes are:
![]()
And so
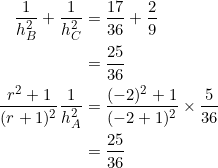
The slopes of sides ![]() are
are ![]() , respectively. They form a geometric progression in which
, respectively. They form a geometric progression in which ![]() . As per our arrangement, we’ll take
. As per our arrangement, we’ll take ![]() and
and ![]() . Therefore the three altitudes are:
. Therefore the three altitudes are:
![]()
And so
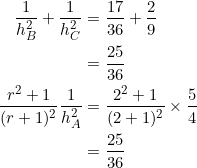
Familiar, friendly, and trendy. Set
![]()
Therefore, any triangle ![]() whose side-slopes form a geometric progression with common ratio
whose side-slopes form a geometric progression with common ratio ![]() will have three altitudes satisfying
will have three altitudes satisfying ![]() . One such triangle has vertices at
. One such triangle has vertices at ![]() ,
, ![]() , and
, and ![]() .
.
Familiar, friendly, trendy, and easy. Set
![]()
Therefore, any triangle ![]() whose side-slopes form a geometric progression with common ratio
whose side-slopes form a geometric progression with common ratio ![]() will have three altitudes satisfying
will have three altitudes satisfying ![]() . One such triangle has vertices at
. One such triangle has vertices at ![]() ,
, ![]() , and
, and ![]() . And there are many — infinitely many — others.
. And there are many — infinitely many — others.
Takeaway
In terms of side-lengths, median-lengths, and slopes, we’ve shown how our triangle closely resembles the right type. Today, the list has now grown to include altitudes.
If anything happens to the right triangle, no need to groan because we already got its clone.
Tasks
- PROVE that
 in a
in a  with
with  .
. - Find possible coordinates for the vertices of
 whose three altitudes are related via
whose three altitudes are related via 
- Find possible coordinates for the vertices of
 whose three altitudes are related via
whose three altitudes are related via 
- For
 with vertices at
with vertices at  ,
,  , and
, and  , verify that:
, verify that:
- the slopes form a geometric progression with common ratio
 ;
;  ;
; .
.
- the slopes form a geometric progression with common ratio
- (Triple arithmetic) For any triangle in which the slopes of the sides form a geometric progression with common ratio
 satisfying
satisfying  , PROVE that:
, PROVE that:
- the squares of the side-lengths form an arithmetic progression;
- the squares of the median-lengths form an arithmetic progression;
- the reciprocals of the squares of the the altitude-lengths form an arithmetic progression.
(An equilateral triangle belongs here. But there are scalene triangles that belong here too. A right isosceles triangle in which satisfies the first and third conditions above.)
satisfies the first and third conditions above.)