For ![]() in which sides
in which sides ![]() have slopes
have slopes ![]() , respectively, the equation connecting their side lengths is
, respectively, the equation connecting their side lengths is
(1) ![]()
as we saw a post ago. The equation connecting their median lengths is
(2) ![]()
and is today’s goal.
Compare the relationship between the medians of a right triangle with the medians of a triangle with slopes ![]() .
.
This is the final, knockout round of our compare-contrast-contest with the right triangle. The contest started on June 28, with the right triangle currently having an edge.
- In a right triangle, the medians are related via
 , where
, where  is the length of the median to the hypotenuse (see the exercises). The triangle with slopes
is the length of the median to the hypotenuse (see the exercises). The triangle with slopes  doesn’t satisfy this relation, unless we put
doesn’t satisfy this relation, unless we put  in (2).
in (2).
Winner: Right triangle; Score is .
. - The previous score was
 , in favour of the right triangle.
, in favour of the right triangle.
Final verdict: Right triangle wins ![]() on aggregate. Case closed.
on aggregate. Case closed.
We still celebrate the triangle with slopes ![]() , despite been rightly trounced by the right triangle.
, despite been rightly trounced by the right triangle.
Consider ![]() with vertices
with vertices ![]() ,
, ![]() , and
, and ![]() . Verify that three medians satisfy equation (2).
. Verify that three medians satisfy equation (2).
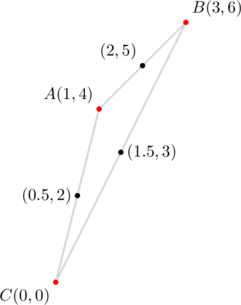
Note that the slopes of sides ![]() are
are ![]() , respectively. They form a geometric progression with
, respectively. They form a geometric progression with ![]() . The midpoints of these sides have been marked. Thus, by the distance formula:
. The midpoints of these sides have been marked. Thus, by the distance formula:
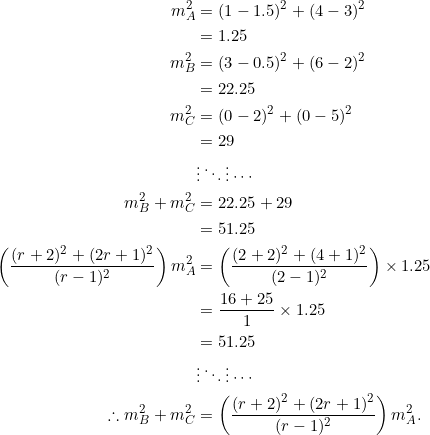
YEA.
Consider ![]() with vertices at
with vertices at ![]() ,
, ![]() , and
, and ![]() . Verify that the three medians satisfy equation (2).
. Verify that the three medians satisfy equation (2).
Easy-peasy. Observe that the slopes of sides ![]() are
are ![]() . They form a geometric progression with common ratio
. They form a geometric progression with common ratio ![]() . Let’s draw a diagram:
. Let’s draw a diagram:
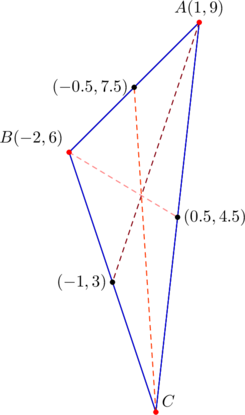
The median lengths then follow by the distance formula. We have:
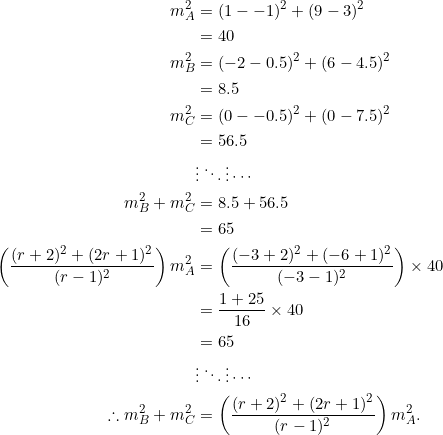
There we go. The formula works for both positive and negative common ratios.
In ![]() , the median lengths are related via
, the median lengths are related via ![]() . Find (possible) coordinates for the vertices
. Find (possible) coordinates for the vertices ![]() .
.
Try solving this problem in a way other than what we present below.
In (2), set ![]() and solve for
and solve for ![]() :
:
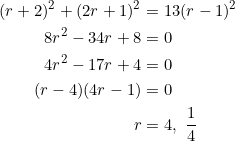
The workload reduces to finding coordinates for a triangle whose slopes form a geometric progression with common ratio ![]() .
.
Easy-peasy.
Among the many options we have for the vertices of a triangle with side slopes ![]() , we can take
, we can take ![]() ,
, ![]() , and
, and ![]() With
With ![]() , these become
, these become ![]() ,
, ![]() , and
, and ![]() . Use these as
. Use these as ![]() . That is, take
. That is, take ![]() ,
, ![]() , and
, and ![]() as the triangle’s vertices. A quick calculation shows that
as the triangle’s vertices. A quick calculation shows that ![]() ,
, ![]() , and
, and ![]() (as in, triple three).
(as in, triple three).
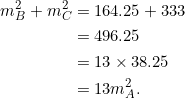
Watch what happens when ![]() in both (1) and (2).
in both (1) and (2).
Put ![]() in (1). Obtain
in (1). Obtain ![]() .
.
Put ![]() in (2). Obtain
in (2). Obtain ![]() .
.
These are well-known, equivalent conditions for the medians from ![]() and
and ![]() to be perpendicular.
to be perpendicular.
Is it surprising that it’s our favourite ![]() -value that saved the day?
-value that saved the day?
For ![]() , let
, let ![]() . Evaluate
. Evaluate ![]() , and show that they are all sums of two consecutive squares.
, and show that they are all sums of two consecutive squares.
Observe that the only integer values of ![]() that produce integer values of
that produce integer values of ![]() are
are ![]() .
.
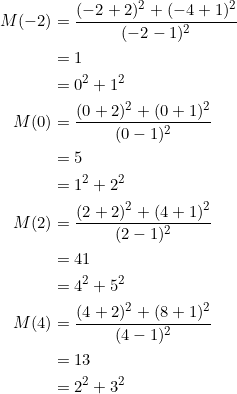
In addition, ![]() defines a bijection
defines a bijection ![]() .
.
In ![]() , we have
, we have ![]() and
and ![]() . Find the value of
. Find the value of ![]() .
.
You can suspect what ![]() will be. From (1) and (2), set
will be. From (1) and (2), set
![]()
Clear fractions, and simplify to obtain the quartic polynomial equation
![]()
The second quadratic factor, ![]() , is really irreducible (its discriminant is
, is really irreducible (its discriminant is ![]() ). So the only real roots come from the first one:
). So the only real roots come from the first one:
![]()
Thus, for ![]() , we have:
, we have:
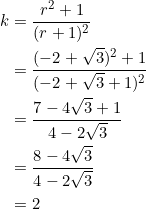
Similarly, for ![]() , we have:
, we have:
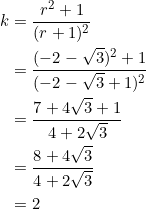
The value of ![]() is
is ![]() , as you may have correctly guessed.
, as you may have correctly guessed.
OK, the above approach was definitely an over![]() ill for something that can be obtained in a simpler way, but it just confirms that our theory conforms to what is more established. See the next example for a better strategy.
ill for something that can be obtained in a simpler way, but it just confirms that our theory conforms to what is more established. See the next example for a better strategy.
In any ![]() , PROVE that the following two statements are equivalent:
, PROVE that the following two statements are equivalent:
- the relations
 and
and  hold simultaneously;
hold simultaneously;  .
.
Consider ![]() and let’s default to standard notation. Use the fact that the median lengths are related to the side lengths via:
and let’s default to standard notation. Use the fact that the median lengths are related to the side lengths via:
(3) 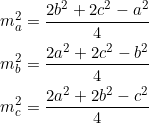
from which ![]() . Now, since
. Now, since ![]() , this becomes
, this becomes ![]() . Also,
. Also, ![]() becomes
becomes ![]() . Since
. Since ![]() , we have:
, we have:
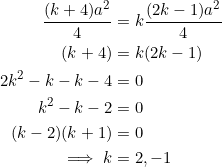
In view of ![]() , we see that
, we see that ![]() can’t be negative (in fact,
can’t be negative (in fact, ![]() : example 10), so discard
: example 10), so discard ![]() , and take
, and take ![]() as the only valid solution. Thus,
as the only valid solution. Thus, ![]() .
.
To see that ![]() , suppose that
, suppose that ![]() . Assume that
. Assume that ![]() . We’ll show that
. We’ll show that ![]() as well. Indeed, from (3):
as well. Indeed, from (3):
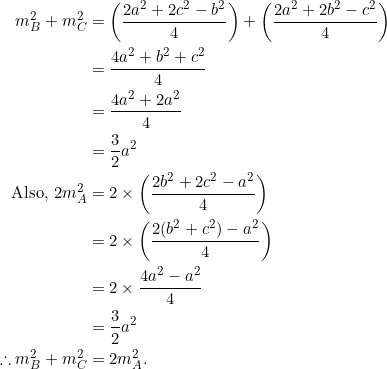
Similarly, if we started with ![]() , we’ll again arrive at
, we’ll again arrive at ![]() . This proves
. This proves ![]() .
.
Bottom line: the two statements are equivalent as claimed.
Kindly bear with us for switching back and forth between the standard notation ![]() and
and ![]() . Hopefully this doesn’t cause any confusion.
. Hopefully this doesn’t cause any confusion.
In any ![]() , if
, if ![]() and
and ![]() , PROVE that
, PROVE that ![]() .
.
The relationship
![]()
holds in any triangle. Using the fact that ![]() and
and ![]() , we have:
, we have:
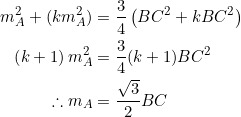
Although we freely cancelled out the common factor ![]() , it shouldn’t obscure the fact that the relations
, it shouldn’t obscure the fact that the relations ![]() and
and ![]() hold simultaneously only when
hold simultaneously only when ![]() .
.
If ![]() , PROVE that
, PROVE that ![]() .
.
Compare with exercise 5 below.
For the proof, begin with one of the expressions in (3):
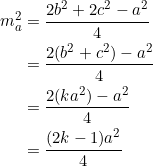
Since the left side ![]() is positive, so must the right side be, and we only have to impose this restriction on the nonkonstant
is positive, so must the right side be, and we only have to impose this restriction on the nonkonstant ![]() .
.
![]() , as desired.
, as desired.
Takeaway
In the equation
![]()
the median from vertex ![]() and the median from vertex
and the median from vertex ![]() are perpendicular only when
are perpendicular only when ![]() . If the focus shifts to the medians from
. If the focus shifts to the medians from ![]() and
and ![]() , or the medians from
, or the medians from ![]() and
and ![]() , then other values of
, then other values of ![]() can still ensure perpendicularity.
can still ensure perpendicularity.
Tasks
- Find possible coordinates for the vertices of
 if its three medians are related via
if its three medians are related via  .
. - Find possible coordinates for the vertices of
 if its three medians are related via
if its three medians are related via  .
. - PROVE that the medians in a right triangle are related via
 , where
, where  is the length of the median to the hypotenuse.
is the length of the median to the hypotenuse. - Derive equation (2).
- Let
 and
and  . PROVE that both
. PROVE that both  and
and  have the same minimum value, but that their common minimum occurs at different values of
have the same minimum value, but that their common minimum occurs at different values of  .
. - Consider the rational function
 :
:
- Verify equation (2) for a triangle with vertices at
 ,
,  , and
, and  .
. - PROVE that if a right triangle has slopes in geometric progression with common ratio
 , then both the squares of the median lengths and the squares of the side lengths form arithmetic progressions.
, then both the squares of the median lengths and the squares of the side lengths form arithmetic progressions. - PROVE that the “mapping”
 , is not well-defined. What modifications should be made to the domain or range, so that the mapping can be well-defined?
, is not well-defined. What modifications should be made to the domain or range, so that the mapping can be well-defined? - If
 and
and  , PROVE that
, PROVE that  is then a sum of two consecutive squares.
is then a sum of two consecutive squares.