A depressed cubic, followed by two special quadratics, and now a special rational function:
(1) ![]()
Everything about our triangle is special. For anyone without clue as to how the above rational function can be construed from a geometric point of view, our triangle is here to the rescue.
Slipshod notation
Let ![]() be such that sides
be such that sides ![]() have slopes
have slopes ![]() , as usual.
, as usual.
Denote the length of the altitude from vertex ![]() by
by ![]() and the length of the median from vertex
and the length of the median from vertex ![]() by
by ![]() . We prove the following height-median-ratio:
. We prove the following height-median-ratio:
(2) ![]()
Simple deductions
Example
PROVE that ![]() .
.
We expect this to be the case — ![]() is the altitude from vertex
is the altitude from vertex ![]() , so it is a shorter distance compared to
, so it is a shorter distance compared to ![]() .
.
Alternatively, we can use the most basic form of the AGM inequality:
![]()
Suppose that the sides ![]() of
of ![]() have slopes
have slopes ![]() , respectively. PROVE that the length of the altitude from vertex
, respectively. PROVE that the length of the altitude from vertex ![]() coincides with the length of the median from vertex
coincides with the length of the median from vertex ![]() if and only if
if and only if ![]() .
.
Obviously, if ![]() , then the geometric progression is essentially
, then the geometric progression is essentially ![]() . These slopes yield an isosceles triangle, from which the conclusion follows.
. These slopes yield an isosceles triangle, from which the conclusion follows.
The advantage of having equation (2) is that it allows for “algebraic” argument. For example, recall that ![]() . If
. If ![]() , then
, then ![]() . That is,
. That is, ![]() . And so
. And so ![]() . Conversely, if
. Conversely, if ![]() , then
, then ![]() .
.
Systematic derivation
Many of the nice properties of triangles with slopes in geometric progression (![]() ) hinge on the following relations among the coordinates (
) hinge on the following relations among the coordinates (![]() ):
):
(3) ![]()
In particular, what we establish below depend on these relations.
Let ![]() ,
, ![]() , and
, and ![]() be the vertices of
be the vertices of ![]() in which sides
in which sides ![]() have slopes
have slopes ![]() . PROVE that
. PROVE that ![]() .
.
Normally, ![]() . Using (3), we get:
. Using (3), we get:
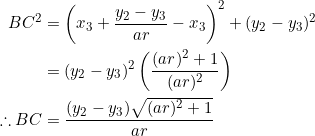
Let ![]() ,
, ![]() , and
, and ![]() be the vertices of
be the vertices of ![]() in which sides
in which sides ![]() have slopes
have slopes ![]() . Find the equation of the altitude from vertex
. Find the equation of the altitude from vertex ![]() .
.
The slope of the altitude from vertex ![]() is
is ![]() , since the slope of side
, since the slope of side ![]() is
is ![]() . Thus the equation of this altitude is
. Thus the equation of this altitude is
![]()
Using the expressions for ![]() and
and ![]() in equation (3), we obtain:
in equation (3), we obtain:
(4) ![]()
Let ![]() ,
, ![]() , and
, and ![]() be the vertices of
be the vertices of ![]() in which sides
in which sides ![]() have slopes
have slopes ![]() . Find the coordinates of the foot of the altitude from vertex
. Find the coordinates of the foot of the altitude from vertex ![]() .
.
The equation of side ![]() is
is ![]() . The altitude from vertex
. The altitude from vertex ![]() has equation given by (4), namely:
has equation given by (4), namely:
![]()
Solving, we obtain
![]()
Let ![]() ,
, ![]() , and
, and ![]() be the vertices of
be the vertices of ![]() in which sides
in which sides ![]() have slopes
have slopes ![]() . PROVE that length of the altitude from vertex
. PROVE that length of the altitude from vertex ![]() is
is ![]() .
.
We find the distance ![]() from
from ![]() to the foot of the altitude
to the foot of the altitude
![]()
The ![]() -difference is
-difference is
![]()
The ![]() -difference is
-difference is
![]()
By the distance formula:
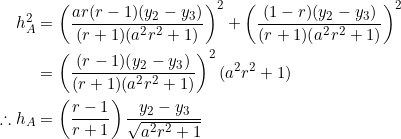
Let ![]() ,
, ![]() , and
, and ![]() be the vertices of
be the vertices of ![]() in which sides
in which sides ![]() have slopes
have slopes ![]() . PROVE the height-median-ratio:
. PROVE the height-median-ratio: ![]() .
.
We use example 3 and example 6 and part of our previous post:
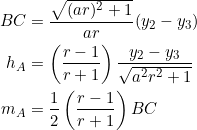
to obtain
![]()
and then
![]()
Sample applications
No doubt you already know the drill.
Find coordinates for the vertices of a ![]() in which the length of the altitude from vertex
in which the length of the altitude from vertex ![]() is
is ![]() the length of the median from vertex
the length of the median from vertex ![]() .
.
Without the organized procedure that equation (2) provides, solving this type of problem may be somewhat random. So as our custom is, we use what we’ve got. In equation (2), set
![]()
and solve the resulting quadratic for ![]() :
:
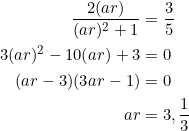
Fix ![]() . It now remains to find the first and third terms of a geometric progression with second term
. It now remains to find the first and third terms of a geometric progression with second term ![]() . For simplicity, let’s choose
. For simplicity, let’s choose ![]() . Then the third term will be
. Then the third term will be ![]() . The basic set of coordinates are:
. The basic set of coordinates are:
![]()
Choose ![]() so that the slopes of
so that the slopes of ![]() are
are ![]() as per our set up. The length of the median from vertex
as per our set up. The length of the median from vertex ![]() is
is ![]() , and the length of the altitude from vertex
, and the length of the altitude from vertex ![]() is
is ![]() .
.
Find coordinates for the vertices of a ![]() in which the length of the altitude from vertex
in which the length of the altitude from vertex ![]() is
is ![]() the length of the median from vertex
the length of the median from vertex ![]() .
.
In equation (2), set
![]()
and solve the resulting quadratic for ![]() :
:
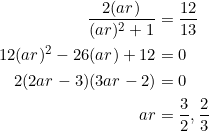
Fix ![]() . We now want a three-term geometric progression with
. We now want a three-term geometric progression with ![]() as the second term. For simplicity, choose
as the second term. For simplicity, choose ![]() . Then we have
. Then we have ![]() as the progression. The corresponding coordinates, using the most basic form, will be
as the progression. The corresponding coordinates, using the most basic form, will be ![]() ,
, ![]() , and
, and ![]() .
.
![]() has coordinates at
has coordinates at ![]() ,
, ![]() ,
, ![]() . Find the length of the altitude from vertex
. Find the length of the altitude from vertex ![]() .
.
The side-slopes are ![]() for
for ![]() . They form a geometric progression in which
. They form a geometric progression in which ![]() and
and ![]() . The length of the altitude from vertex
. The length of the altitude from vertex ![]() in such a case is given (see example 6) by
in such a case is given (see example 6) by
![]()
Takeaway
Be careful with the sign of ![]() in the rational expression:
in the rational expression:
![]()
because ![]() can be negative, whereas the ratio on the left is positive.
can be negative, whereas the ratio on the left is positive.
Note also that the “strange” formulas we state work only in the case of triangles with slopes in geometric progression. (By the way, it now seems that these triangles provide a platform for studying some basic functions.)
Tasks
- PROVE that if the coordinates of a triangle’s vertices are related according to (3), then its side-slopes form a geometric progression.
- Let
 as in equation (1). For
as in equation (1). For  , PROVE that
, PROVE that  .
. - Consider
 in which
in which  unit and
unit and  units. If
units. If  , PROVE that
, PROVE that  .
. - Find coordinates for the vertices of a triangle
 in which the length of the altitude from vertex
in which the length of the altitude from vertex  is
is  the length of the median from vertex
the length of the median from vertex  .
. - (Explicit error) Find coordinates for the vertices of
 for which the length of the altitude from vertex
for which the length of the altitude from vertex  is twice the length of the median from vertex
is twice the length of the median from vertex  .
.