(1) ![]()
will be outlined in example 9, and will span (about) nine lines. Meanwhile, the formula and the title are not quite aligned ![]()
Copious verification
In equation (1) above, ![]() is the length of the median from vertex
is the length of the median from vertex ![]() , and
, and ![]() is the length of side
is the length of side ![]() . Our first four examples confirm that the relation (1) should hold for all values of
. Our first four examples confirm that the relation (1) should hold for all values of ![]() , except the unwanted ones:
, except the unwanted ones: ![]()
Example
Consider ![]() with vertices at
with vertices at ![]() ,
, ![]() , and
, and ![]() . Find the length of the median from vertex
. Find the length of the median from vertex ![]() , and verify that equation (1) is satisfied.
, and verify that equation (1) is satisfied.
The slopes of sides ![]() are
are ![]() , respectively. They form a geometric progression in which
, respectively. They form a geometric progression in which ![]() .
.
Let’s first find the length of the median from vertex ![]() . The midpoint of side
. The midpoint of side ![]() is at
is at ![]() . Together with
. Together with ![]() , the distance formula gives:
, the distance formula gives:
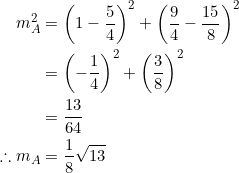
Thus, the length of the median from vertex ![]() is
is ![]() .
.
Next, the length of side ![]() is, by the distance formula:
is, by the distance formula:
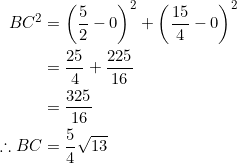
Finally, we check that both ![]() and
and ![]() are related via equation (1):
are related via equation (1):
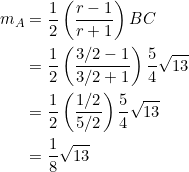
Expected.
Example
Consider ![]() with vertices at
with vertices at ![]() ,
, ![]() , and
, and ![]() . Find the length of the median from vertex
. Find the length of the median from vertex ![]() and verify that equation (1) is satisfied.
and verify that equation (1) is satisfied.
The slopes of sides ![]() are
are ![]() , respectively. They form a geometric progression in which
, respectively. They form a geometric progression in which ![]() . Special, special case.
. Special, special case.
The midpoint of side ![]() is at
is at ![]() . Together with
. Together with ![]() , we can find the length of the median from vertex
, we can find the length of the median from vertex ![]() :
:
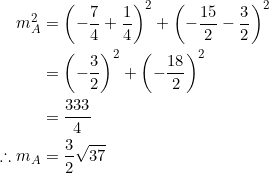
With ![]() at
at ![]() and
and ![]() at
at ![]() :
:
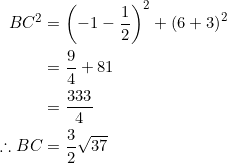
Surprised — that ![]() .
.
If we put ![]() in equation (1) we see that
in equation (1) we see that
![]()
Surprise no longer applies. Subtract surprise from your dictionary.
If the slopes of the sides of a triangle form a geometric progression with common ration ![]() , then one median and the side opposite it are equal in length.
, then one median and the side opposite it are equal in length.
Example
Consider ![]() with vertices at
with vertices at ![]() ,
, ![]() , and
, and ![]() . Find the length of the median from vertex
. Find the length of the median from vertex ![]() , and verify that equation (1) is satisfied.
, and verify that equation (1) is satisfied.
The slopes of sides ![]() are
are ![]() , respectively. They form a geometric progression in which
, respectively. They form a geometric progression in which ![]() .
.
The midpoint of side ![]() is at
is at ![]() . Together with
. Together with ![]() , we find:
, we find:
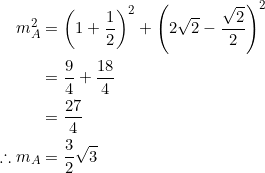
With ![]() at
at ![]() and
and ![]() at
at ![]() :
:
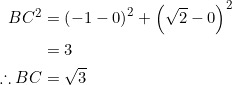
Put ![]() in equation (1):
in equation (1):
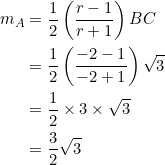
YESpected.
Example
Consider ![]() with vertices at
with vertices at ![]() ,
, ![]() , and
, and ![]() . Find the length of the median from vertex
. Find the length of the median from vertex ![]() , and verify that equation (1) is satisfied.
, and verify that equation (1) is satisfied.
Our examples will be incomplete without this ugly, lovely triangle.
The midpoint of side ![]() is at
is at ![]() . Together with
. Together with ![]() :
:
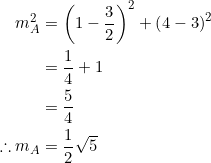
With ![]() at
at ![]() and
and ![]() at
at ![]() , the length of
, the length of ![]() is seen to be
is seen to be
![]()
Since the slopes of the sides of ![]() form a geometric progression with common ratio
form a geometric progression with common ratio ![]() , let’s put
, let’s put ![]() in equation (1):
in equation (1):
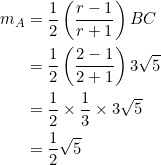
Passed.
Obvious observations
Maybe you’ve wondered why we omitted absolute value in equation (1):
![]()
Wonder no more.
Example
If ![]() , PROVE that
, PROVE that ![]() .
.
This is because ![]() , and
, and ![]() , so the quotient
, so the quotient ![]() is also greater than
is also greater than ![]() .
.
Example
If ![]() , PROVE that
, PROVE that ![]() .
.
If ![]() , then we have
, then we have ![]() and also
and also ![]() . So the quotient
. So the quotient ![]() .
.
Example
If ![]() , PROVE that
, PROVE that ![]()
If ![]() , then
, then ![]() . The fact that
. The fact that ![]() ensures that
ensures that ![]() . So the numerator and denominator of
. So the numerator and denominator of ![]() have negative and positive signs, respectively. This makes the quotient negative.
have negative and positive signs, respectively. This makes the quotient negative.
However, if the common ratio of our three-term geometric progression happens to be sandwiched between ![]() and
and ![]() , we can simply use its reciprocal — which will then satisfy
, we can simply use its reciprocal — which will then satisfy ![]() — in equation (1). This is the case of Example 5.
— in equation (1). This is the case of Example 5.
Example
If ![]() , PROVE that
, PROVE that ![]() .
.
If ![]() , then
, then ![]() . If in addition
. If in addition ![]() , then adding
, then adding ![]() to both sides of the inequality gives
to both sides of the inequality gives ![]() . So the numerator and denominator of
. So the numerator and denominator of ![]() are negative and positive, respectively. This makes the quotient to be negative.
are negative and positive, respectively. This makes the quotient to be negative.
However, if the common ratio of our three-term geometric progression happens to be sandwiched between ![]() and
and ![]() , then we can simply use its reciprocal — which will then satisfy
, then we can simply use its reciprocal — which will then satisfy ![]() — in equation (1). This is the case of Example 6.
— in equation (1). This is the case of Example 6.
Tedious derivation
As we derive equation (1) in what follows, are we really being serious by hinting that the procedure is tedious? Follow us to see that the answer is obvious.
PROVE that equation (1) holds for any triangle ![]() with slopes
with slopes ![]() for the sides
for the sides ![]() .
.
We’ll use two identities from our previous posts:
(2) 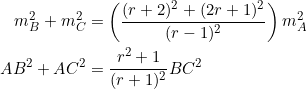
and a well-known identity, namely
![]()
which holds for any triangle. We’ll write the latter in the form
(3) ![]()
Eliminate ![]() from equations (2) and (3):
from equations (2) and (3):
![]()
Isolate ![]() and continue the algebra:
and continue the algebra:
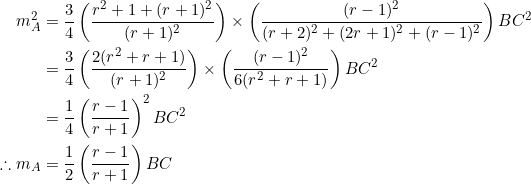
Just as we said.
Find coordinates for the vertices ![]() of a
of a ![]() in which the length of one median is one-third of the length of the opposite side.
in which the length of one median is one-third of the length of the opposite side.
We want a triangle ![]() in which
in which ![]() , for example. Without recourse to equation (1), solving this problem maybe somewhat random.
, for example. Without recourse to equation (1), solving this problem maybe somewhat random.
So we’ll use what we’ve got. In (1), set
![]()
and solve for ![]() :
: ![]() .
.
It remains to find coordinates for the vertices of a triangle in which the slopes of the sides form a geometric progression with common ratio ![]() .
.
Use the most basic set of coordinates for the vertices:
That’s it. ![]() with vertices above is what we want:
with vertices above is what we want:
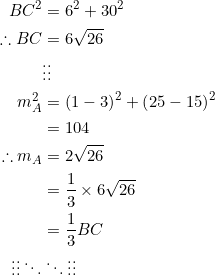
Takeaway
Our main equation (1)
![]()
is similar to what happens in a right triangle, where the length of the median to the hypotenuse is half of the length of the hypotenuse.
Tasks
- Find coordinates for the vertices of
 in which one median has length equal to
in which one median has length equal to  of the length of the opposite side.
of the length of the opposite side. - Find coordinates for the vertices of a right triangle in which the side-slopes form a geometric progression with common ratio
 .
. - (Polynomial equations) Let
 be such that sides
be such that sides  have slopes
have slopes  , respectively. PROVE that:
, respectively. PROVE that:
 , if
, if  ;
; , if
, if  ;
; , if
, if  .
.
- (Confusing notation) In any
 with vertices
with vertices  ,
,  , and
, and  , let the slopes of the medians be denoted by
, let the slopes of the medians be denoted by  , and let the slopes of the sides be
, and let the slopes of the sides be  . PROVE that:
. PROVE that:
 ;
; .
.
(In our slipshod style, we sometimes use to denote the length of a median and sometimes the slope of the same median. Are we short of notations?)
to denote the length of a median and sometimes the slope of the same median. Are we short of notations?)
- (Alternative derivation) Let
 be equilateral such that sides
be equilateral such that sides  have slopes
have slopes  , respectively. PROVE that:
, respectively. PROVE that:
 ;
; .
.
(You can apply exercise 3 above, which uses a different approach compared to what we did in a previous post.)
- (Linear combinations) Let
 ,
,  , and
, and  be the vertices of
be the vertices of  in which sides
in which sides  have slopes
have slopes  . PROVE that
. PROVE that  , and
, and  .
. - Let
 . PROVE that
. PROVE that  is also an integer if, and only if,
is also an integer if, and only if,  .
. - Let
 and consider
and consider  with slopes
with slopes  for sides
for sides  . PROVE that the length
. PROVE that the length  of the median from vertex
of the median from vertex  is an integer multiple of the length of side
is an integer multiple of the length of side  if, and only if,
if, and only if,  .
. - Find appropriate coordinates for the vertices of
 in which the side-slopes form a geometric progression and the length of the median from vertex
in which the side-slopes form a geometric progression and the length of the median from vertex  is twice the length of side
is twice the length of side  .
. - Give an example of a triangle
 in which the length of the median from vertex
in which the length of the median from vertex  is equal to the length of side
is equal to the length of side  , but the slopes of the sides do not form a geometric progression. (This shows that the converse of example 2 is not true.)
, but the slopes of the sides do not form a geometric progression. (This shows that the converse of example 2 is not true.)