Sloppy slopes swap sequences – High School Geometry

As shown by our slipshod, tongue-twisting title, slopes can be very “brittle”.

We demonstrate how to convert the slopes of the sides of a triangle from a geometric sequence to an arithmetic sequence. Hopefully it makes sense.

Modified midpoint theorem

A line which connects the midpoints of two sides of a triangle is parallel to the third side and its length is half of the third side’s length. So says the midpoint theorem.

Since a midpoint amounts to dividing a line segment in the ratio $1:1$ , we’ll modify this slightly for our triangle and rather divide the sides in the $r$ atio $1:r$ , whe $r$ e $~1\neq r> 0$ .

In $\triangle ABC$ , let $X$ and $Y$ be points on $BA$ and $CA$ which divide the sides in the ratio $1:n$ , where $n$ is a positive integer. PROVE that the line segment $XY$ is parallel to $BC$ and that $XY=\frac{n}{n+1}BC$ .

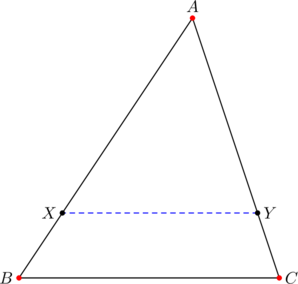
In the diagram above, $BX:XA=1:n$ and $CY:YA=1:n$ . If we place the vertices of $\triangle ABC$ at $A(x_1,y_1)$ , $B(x_2,y_2)$ , and $C(x_3,y_3)$ , then we can obtain the coordinates of points $X$ and $Y$ using the formula for internal division of a line segment:

$X\left(\frac{x_1+nx_2}{n+1},\frac{y_1+ny_2}{n+1}\right),~Y\left(\frac{x_1+nx_3}{n+1},\frac{y_1+ny_3}{n+1}\right).$

The slope of line segment $XY$ is:

$\begin{equation*} \begin{split} &=\left[\frac{y_1+ny_2}{n+1}-\left(\frac{y_1+ny_3}{n+1}\right)\right]\div\left[\frac{x_1+nx_2}{n+1}-\left(\frac{x_1+nx_3}{n+1}\right)\right]\\ &=\frac{n}{n+1}(y_2-y_3)\div\left(\frac{n}{n+1}(x_2-x_3)\right)\\ &=\frac{y_2-y_3}{x_2-x_3} \end{split} \end{equation*}$

So $XY$ is parallel to $BC$ . In addition we obtain $XY=\frac{n}{n+1}BC$ .

Easy-peasy.

Derailing development

If we apply the above idea to our own triangle, look what we get.

Suppose that $\triangle ABC$ has vertices $A(x_1,y_1)$ , $B(x_2,y_2)$ , $C(x_3,y_3)$ , and slopes $a,ar,ar^2$ for sides $AB,BC,CA$ , respectively. For $1\neq r> 0$ , find coordinates for the point which divides $AB$ in the ratio $1:r$ .

Note the “direction” of the division. The desired point will be $\left(\frac{x_2+rx_1}{r+1},\frac{y_2+ry_1}{r+1}\right)$ , using the formula for internal division of a line segment. In view of the $r$ elationship among the coordinates, this becomes

$\left(x_3+\frac{(2r+1)(y_2-y_3)}{ar(r+1)^2},\frac{(r^2+r+1)y_2+ry_3}{(r+1)^2}\right).$

You see that quadratic rearing its beautiful head again?

Ordinarily, this would be the point $\left(\frac{x_2+rx_3}{r+1},\frac{y_2+ry_3}{r+1}\right)$ . Using the $r$ elationship among the coordinates, we get

$\left(x_3+\frac{y_2-y_3}{ar(r+1)},\frac{ry_2+y_3}{r+1}\right)$

This would be the point $\left(\frac{x_1+rx_3}{r+1},\frac{y_1+ry_3}{r+1}\right)$ . The $r$ elationship among the coordinates then gives

$\left(x_3+\frac{y_2-y_3}{ar(r+1)^2},\frac{ry_2+(r^2+r+1)y_3}{(r+1)^2}\right)$

(Main goal)

Suppose that $\triangle ABC$ has vertices $A(x_1,y_1)$ , $B(x_2,y_2)$ , $C(x_3,y_3)$ , and slopes $a,ar,ar^2$ for sides $AB,BC,CA$ , respectively. For $1\neq r> 0$ , PROVE that there is a point $X$ on $AB$ , a point $Y$ on $BC$ , and a point $Z$ on $CA$ such that the slopes of the sides of $\triangle XYZ$ form an arithmetic progression.

Basically, the side-slopes form a geometric progression, while the sub-triangle’s side-slopes form an arithmetic progression. Fo $r$ . Any. $1\neq r> 0$ .

Let $X$ be the point which divides $AB$ in the ratio $1:r$ , let $Y$ be the point which divides $CB$ in the ratio $1:r$ , and let $Z$ be the point which divides $CA$ in the ratio $1:r$ . As in the three preceding examples, these points are:

$\begin{equation*} \begin{split} X&\left(x_3+\frac{(2r+1)(y_2-y_3)}{ar(r+1)^2},\frac{(r^2+r+1)y_2+ry_3}{(r+1)^2}\right)\\ Y&\left(x_3+\frac{y_2-y_3}{ar(r+1)},\frac{ry_2+y_3}{r+1}\right)\\ Z&\left(x_3+\frac{y_2-y_3}{ar(r+1)^2},\frac{ry_2+(r^2+r+1)y_3}{(r+1)^2}\right) \end{split} \end{equation*}$

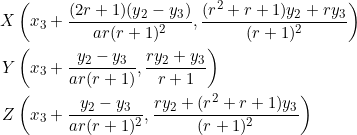
By the modified midpoint theorem, $XY$ would be parallel to $CA$ , so its slope is $ar^2$ (alternatively can be confirmed by direct calculation). Similarly, $YZ$ would be parallel to $AB$ , so its slope is $a$ .

By direct calculation, the slope of $ZX$ is $\frac{a+ar^2}{2}$ .

Thus, the slopes of the sides of $\triangle XYZ$ are $a,\frac{a+ar^2}{2},ar^2$ , an arithmetic progression.

Given $\triangle ABC$ with vertices at $A(1,4)$ , $B(3,6)$ , and $C(0,0)$ , find coordinates for points $X,Y,Z$ on $AB,BC,CA$ such that the slopes of $\triangle XYZ$ are $1,\frac{5}{2},4$ .

Observe that the slopes of sides $AB,BC,CA$ are $1,2,4$ , respectively.

Thus, by Example 5, let $X$ be the point which divides $AB$ in the ratio $1:2$ , let $Y$ be the point which divides $CB$ in the ratio $1:2$ , and let $Z$ be the point which divides $CA$ in the ratio $1:2$ . Lots of repetitions there $\cdots$ .

Using the formula for internal division of a line segment, we find these points to be $X\left(\frac{5}{3},\frac{14}{3}\right)$ , $Y(1,2)$ , and $Z\left(\frac{1}{3},\frac{4}{3}\right)$ . Then:

$\begin{equation*} \begin{split} \textrm{slope of}~XY&=4\\ \textrm{slope of}~YZ&=1\\ \textrm{slope of}~ZX&=\frac{5}{2} \end{split} \end{equation*}$

Given $\triangle ABC$ with vertices at $A(1,9)$ , $B(4,12)$ , and $C(0,0)$ , find coordinates for points $X,Y,Z$ on $AB,BC,CA$ such that the slopes of $\triangle XYZ$ are $1,5,9$ .

In this case, the slopes of sides $AB,BC,CA$ are $1,3,9$ , respectively. A geometric progression in which $r=3$ .

By Example 5, let $X,Y,Z$ divide each of the three sides $AB,CB,CA$ in the ratio $1:3$ .

Using the formula for internal division of a line segment, we find these points to be $X\left(\frac{7}{4},\frac{39}{4}\right)$ , $Y(1,3)$ , and $Z\left(\frac{1}{4},\frac{9}{4}\right)$ .

$\begin{equation*} \begin{split} \textrm{slope of}~XY&=9\\ \textrm{slope of}~YZ&=1\\ \textrm{slope of}~ZX&=5 \end{split} \end{equation*}$

Given $\triangle ABC$ with vertices at $A(1,4)$ , $B(-1,2)$ , and $C(0,0)$ , find coordinates for (external) points $X,Y,Z$ on $AB,BC,CA$ such that the slopes of $\triangle XYZ$ are $1,\frac{5}{2},4$ .

Observe that the slopes of sides $AB,BC,CA$ are $1,-2,4$ , respectively. They form a geometric progression in which $r=-2$ .

Let $X,Y,Z$ be points which divide $AB,CB,CA$ all in the ratio $1:-2$ . We obtain the external points $X\left(3,6\right)$ , $Y(1,-2)$ , and $Z\left(-1,-4\right)$ . Then:

$\begin{equation*} \begin{split} \textrm{slope of}~XY&=4\\ \textrm{slope of}~YZ&=1\\ \textrm{slope of}~ZX&=\frac{5}{2} \end{split} \end{equation*}$

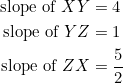
The scene here may be worth seeing $\cdots$

Notice that $C$ is the midpoint of both $AZ$ and $BY$ , while $A$ is the midpoint of $BX$ . It follows that the length of $XY$ is twice that of $AC$ .

Touching negative common ratios, a couple of strangely exciting things happen. This is why we’ve been silent about them in many of our posts, but we have them on our radar and will treat them later.

Let $ABC$ be a right isosceles triangle with slopes $a,ar,ar^2$ . PROVE that there are two points $X$ and $Y$ on sides $AB,AC$ such that the slope of the line segment $XY$ is $-\frac{3}{2}$ times the slope of $BC$ .

By Example 5, we can find points $X,Y,Z$ such that the slopes of the sides of $\triangle XYZ$ are $a,\frac{a+ar^2}{2},ar^2$ .

Using the fact that $r^2+3r+1=0$ for a right isosceles triangle, we have:

$\begin{equation*} \begin{split} \frac{a+ar^2}{2}&=\frac{a(1+r^2)}{2}\\ &=\frac{a(-3r)}{2}\\ &=-\frac{3}{2}(ar)\\ \end{split} \end{equation*}$

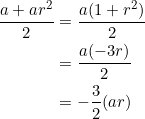
Plus or minus two

Let $ABC$ be an equilateral triangle with slopes $a,ar,ar^2$ . PROVE that there are two points $X$ and $Y$ on two sides such that the slope of the line segment $XY$ is $\pm 2$ .

By Example 5, we can find points $X,Y,Z$ on $AB,BC,CA$ such that the slopes of the sides of $\triangle XYZ$ are $a,\frac{a+ar^2}{2},ar^2$ .

Using the fact that $ar=\pm 1$ and $r^2+4r+1=0$ for an equilateral triangle, we have:

$\begin{equation*} \begin{split} \frac{a+ar^2}{2}&=\frac{a(1+r^2)}{2}\\ &=\frac{a(-4r)}{2}\\ &=-2(ar)\\ &=\pm 2 \end{split} \end{equation*}$

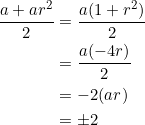
Point-blank.

Takeaway

The construction we’ve done is just a variant of the medial triangle. Unlike the medial triangle, ours is different in the sense that it does not retain the slopes of the parent triangle. While the slopes of the parent triangle form a geometric progression, its own slopes form an arithmetic progression. Talk about t $r$ ansfo $r$ mation.

Tasks

(Two out) Consider $\triangle ABC$ with vertices at $A(1,4)$ , $B(3,6)$ , and $C(0,0)$ . PROVE that one can obtain the infinite arithmetic sequence $\cdots,-3,-2,-1,0,1,\boxed{2},3,\cdots$ as slopes of line segments drawn from vertex $A$ to side $BC$ .
(Notice that $2$ is out because it’s already the slope of side $BC$ . Other than that, every other integer can be obtained this way. What’s somewhat interesting here is that the line segments from $A$ to $BC$ that generate the sequence terms all stay within the triangle; none of them is external.)
(Fibonacci sequence) Explain how the terms of a Fibonacci sequence $0,1,1,2,3,5,8,13,\cdots$ can be generated as slopes.
(Always odd) Let $r$ be a positive integer, and consider $\triangle ABC$ with vertices at $A(1,r^2)$ , $B(0,0)$ , and $C(1+r,r+r^2)$ . PROVE that there is a point $X$ on $AC$ and a point $Y$ on $CB$ such that the slope of the line segment $XY$ is $2r-1$ .
(If $r$ is an integer, then any number of the form $2r-1$ is odd.)
Let be such that sides have slopes . Let be points on which divide these sides all in the ratio . PROVE that:
- the $x$ -coordinates of $\triangle XYZ$ form an arithmetic progression
- the line connecting the centroid of $\triangle XYZ$ to the centroid of $\triangle ABC$ is parallel to side $BC$ .
Find an appropriate choice of coordinates for the vertices of a right isosceles triangle whose side-slopes form a geometric progression.