An inequality in cyclic quadrilaterals

In a cyclic quadrilateral $ABCD$

with diagonals $AC=p$

and $BD=q$

and circumradius $R$

, the quantity $8R^2$

is an upper bound for the sum of the squares of the diagonals; in other words: $\boxed{p^2+q^2\leq 8R^2 .}$

It is only when the parent quadrilateral is a rectangle that equality holds.

Easy proofs

Let $ABCD$

be a cyclic quadrilateral with circumradius $R$

and diagonals $AC=p$

, $BD=q$

. PROVE that $p\sin A=q\sin B$

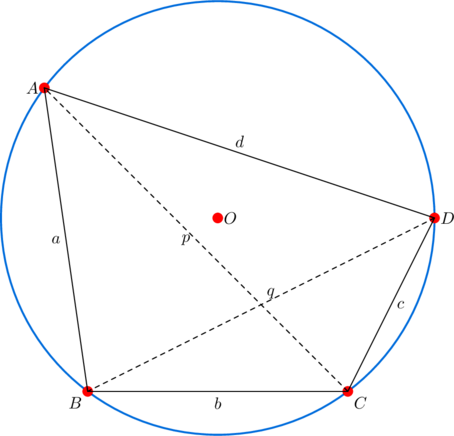
Since triangles $ABC$ and $ABD$ have the same circumradius $R$ we have from the above diagram that $p=2R\sin B$ and $q=2R\sin A$ . Thus $p\sin A=q\sin B=2R\sin A\sin B$ .

Let $ABCD$

be a cyclic quadrilateral with circumradius $R$

and diagonals $AC=p$

, $BD=q$

. PROVE that $p\sin C=q\sin D$

Follows from the previous example, since the opposite angles at $A$ and $C$ , as well as at $B$ and $D$ , ensures that $\sin A=\sin C$ and $\sin B=\sin D$ .

Let $ABCD$

be a cyclic quadrilateral with circumradius $R$

and diagonals $AC=p$

, $BD=q$

. PROVE that $p^2+q^2=4R^2(\sin^2A+\sin^2B)$

We have $p=2R\sin B$ , $q=2R\sin A$ . Thus $p^2+q^2=4R^2(\sin^2A+\sin^2B)$ .

Let $ABCD$

be a cyclic quadrilateral with circumradius $R$

and diagonals $AC=p$

, $BD=q$

. Deduce that $p^2+q^2\leq 8R^2$

Since $p^2+q^2=4R^2(\sin^2A+\sin^2B)$ from the preceding example, and $\sin^2A\leq 1,\sin^2B\leq 1$ , it follows that $p^2+q^2\leq 8R^2$ .

Exclusive property

For rectangles only.

Let $ABCD$

be a cyclic quadrilateral with circumradius $R$

and diagonals $AC=p$

, $BD=q$

. If $p^2+q^2=8R^2$

, PROVE that $ABCD$

is a rectangle.

We always have $p^2+q^2=4R^2(\sin^2A+\sin^2B)$ . If the right side is now $8R^2$ , then we must have $\sin^2A+\sin^2B=2$ . The latter equation can only be satisfied by taking $\sin A=1$ and $\sin B=1$ . Similarly we have $p^2+q^2=4R^2(\sin^2C+\sin^2D)$ , and so $\sin^2C+\sin^2D=2$ . We take $\sin C=\sin D=1$ . Thus, in such a cyclic quadrilateral we have $A=B=C=D=90^{\circ}$ .

Elusive password

Jump straight to the exercises at this stage — or read what follows for a little bit of distraction. As we promised previously, we’ll be bringing you occasional updates about our ongoing hide and seek — or, tug-of-war — game with some unknown bots. The game is exciting because we currently have the ascendancy.

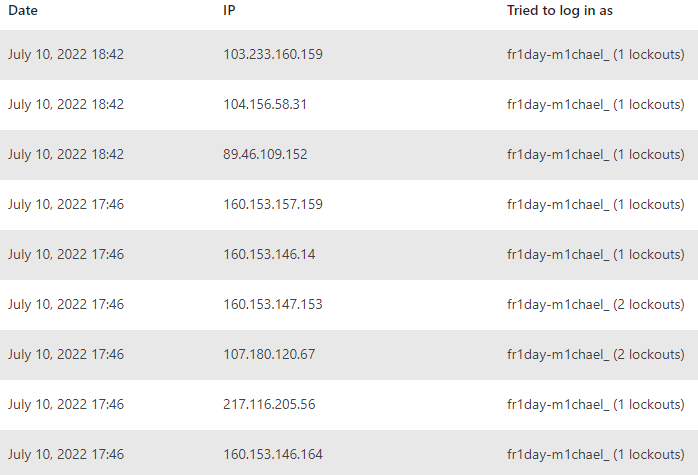
Scene 1: Barrage by bots

Scene 2: Breathe for a bit

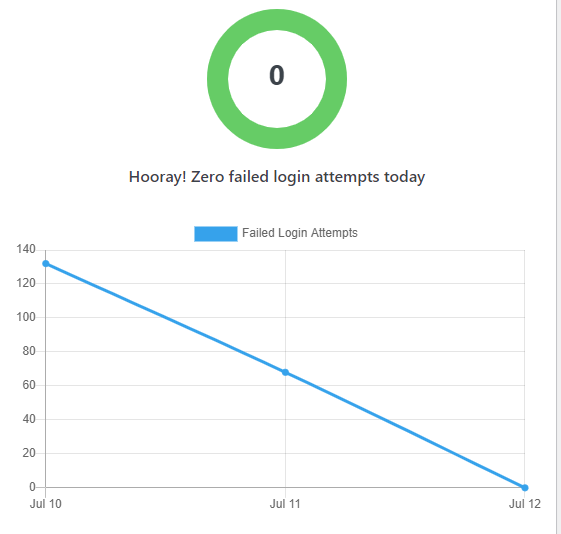
Is any of the above IP addresses familiar?

Takeaway

Let $ABCD$ be a convex cyclic quadrilateral with circumradius $R$ and diagonals $AC=p$ , $BD=q$ . Then the following statements are equivalent:

$ABCD$ is a rectangle
$p^2+q^2=8R^2$ .

Task

(Special case) Let be a convex cyclic quadrilateral with vertices at , , , and . PROVE that:
1. diagonal $AC$ bisects diagonal $BD$
2. $p^2+q^2=4R^2$ , where $AC=p$ and $BD=q$
3. $p^2=2(R^2+x^2)$ and $q^2=2(R^2-x^2)$ , where $x$ is the length of the Newton line.