Let  be a cyclic quadrilateral with side-lengths
be a cyclic quadrilateral with side-lengths  ,
,  ,
,  , and
, and  . Let
. Let  and
and  be the diagonals. Then
be the diagonals. Then  bisects
bisects  if and only if
if and only if  , and
, and  bisects
bisects  if and only if
if and only if  .
.
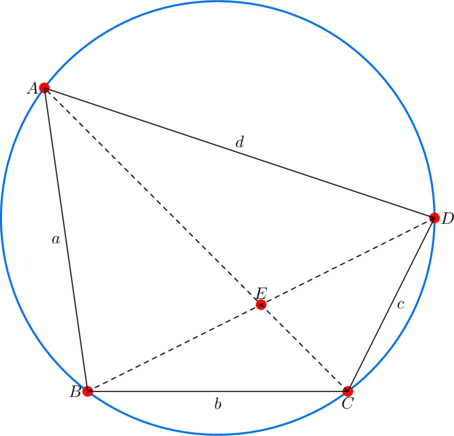
Let  be a convex quadrilateral whose diagonals intersect at
be a convex quadrilateral whose diagonals intersect at  . If
. If  is cyclic, PROVE that
is cyclic, PROVE that  and
and  .
.
Use similar triangles.
Let  be a convex quadrilateral whose diagonals intersect at
be a convex quadrilateral whose diagonals intersect at  . If
. If  and
and  , PROVE that
, PROVE that  is cyclic.
is cyclic.
This is the converse of the previous statement in example 1. One proof of it uses similar triangles and the law of sines.

Let  be a convex cyclic quadrilateral whose diagonals intersect at
be a convex cyclic quadrilateral whose diagonals intersect at  . PROVE that diagonal
. PROVE that diagonal  bisects diagonal
bisects diagonal  if, and only if,
if, and only if,  .
.
By example 1 we have that ![]() . If
. If ![]() bisects
bisects ![]() , then
, then ![]() . And so
. And so ![]() . Similarly for the converse.
. Similarly for the converse.
Let  be a convex cyclic quadrilateral whose diagonals intersect at
be a convex cyclic quadrilateral whose diagonals intersect at  . PROVE that diagonal
. PROVE that diagonal  bisects diagonal
bisects diagonal  if, and only if,
if, and only if,  .
.
By example 1 we have that ![]() . If
. If ![]() bisects
bisects ![]() , then
, then ![]() . And so
. And so ![]() . Similarly for the converse.
. Similarly for the converse.
Among convex cyclic quadrilaterals, PROVE that only rectangles have the two diagonals bisecting each other.
This follows from example 3 and example 4 above, since ![]() and
and ![]() yield
yield ![]() and
and ![]() .
.
Brief relief
Click these links to see the status of our ongoing hide-and-seek game with some hackers and their bots: here, here, and here. Good thing is that we have the upper hand, as at the time of this writing.
Takeaway
Let ![]() be a convex cyclic quadrilateral. Then the following statements are equivalent:
be a convex cyclic quadrilateral. Then the following statements are equivalent:
 is a rectangle
is a rectangle- diagonals
 and
and  bisect each other.
bisect each other.
Task
- (Easy verification) Let
 be a convex cyclic quadrilateral with vertices at
be a convex cyclic quadrilateral with vertices at  ,
,  ,
,  ,
,  . Verify that:
. Verify that:
- diagonal
 bisects diagonal
bisects diagonal 

 .
.
- diagonal